陕西省榆林市2022届高三下学期理数三模试卷
试卷更新日期:2022-04-22 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 若复数在复平面内对应的点位于第一象限,则实数的取值范围为( )A、 B、 C、 D、3. 已知抛物线上的一点到其焦点的距离为2,则该抛物线的焦点到其准线的距离为( )A、6 B、4 C、3 D、24. 已知函数 , 则“”是“是的一个极小值点”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知 , , 是三条不同的直线, , 是两个不同的平面,若 , , , , 则( )A、 B、 C、 D、6. 2021年5月15日7时18分,天问一号探测器成功着陆于火星乌托邦平原南部预选着陆区,我国首次火星探测任务着陆火星取得成功,航天技术得以发展,得益于如下的齐奥尔科大斯基公式: , 其中 , 分别为燃料燃烧前与燃烧后的火箭质量,是燃料喷出的速度,是火箭的初速度,是燃料完全燃尽时火箭的速度,现准备发射一个二级火箭(初速度),每级火箭的箭体结构的质量均为50吨,每级火箭携带的燃料质量均为250吨,燃料喷出的速度为 , 先点燃第一级火箭燃料,燃料燃尽后,第一级火箭自动脱离,同时点燃第二级火箭的燃料,则当第二级火箭的燃料燃尽时,火箭的速度约为( )(参考数据: , )A、 B、 C、 D、7. △的内角 , , 的对边分别为 , , , 若△的面积为 , , , 则( )A、10 B、3 C、 D、8. 某公司计划招聘一批新员工,现有100名应届毕业生应聘,通过考试成绩择优录取,这100人考试成绩的频率分布直方图如图所示,若该公司计划招聘60名新员工,则估计新员工的最低录取成绩为( )
 A、75分 B、78分 C、80分 D、85分9. 四边形为菱形, , , 是菱形所在平面的任意一点,则的最小值为( )A、-30 B、-27 C、-15 D、-910. 在矩形中,以 , 为焦点,经过 , 两点的椭圆和双曲线的离心率分别为 , , 则( )A、 B、 C、 D、与2的大小关系不确定11. 已知是定义在上的函数,是的导函数,且 , , 则下列结论一定成立的是( )A、 B、 C、 D、12. 已知 , 函数在上单调递增,且对任意 , 都有 , 则的取值范围为( )A、 B、 C、 D、
A、75分 B、78分 C、80分 D、85分9. 四边形为菱形, , , 是菱形所在平面的任意一点,则的最小值为( )A、-30 B、-27 C、-15 D、-910. 在矩形中,以 , 为焦点,经过 , 两点的椭圆和双曲线的离心率分别为 , , 则( )A、 B、 C、 D、与2的大小关系不确定11. 已知是定义在上的函数,是的导函数,且 , , 则下列结论一定成立的是( )A、 B、 C、 D、12. 已知 , 函数在上单调递增,且对任意 , 都有 , 则的取值范围为( )A、 B、 C、 D、二、填空题
-
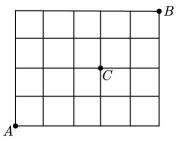
13. 若实数 , 满足约束条件 , 则的最小值为.14. 已知 , 则.15. 在某城市中, , 两地有如图所示的方格型道路网,甲随机沿路网选择一条最短路径,从地出发去往地,且不经过地,则不同的路径共有条.
 16. 某几何体的三视图如图所示,则该几何体外接球的体积为 .
16. 某几何体的三视图如图所示,则该几何体外接球的体积为 .

三、解答题
-
17. 某商场为提高服务质量,随机调查了20名男顾客和20名女顾客,根据每位顾客对该商场服务质量的评分(满分100分)绘制了如图所示的茎叶图.
男顾客
女顾客
8
8
7
5
3
7
2
2
3
3
5
6
7
8
8
7
6
5
5
2
1
8
0
1
2
2
5
7
7
8
9
7
6
5
5
3
0
0
9
0
0
1
2
附: .
0.10
0.05
0.010
0.001
2.706
3.841
6.635
10.828
(1)、根据茎叶图判断男、女顾客中,哪类顾客对该商场的服务质量更认可?并说明理由.(2)、将这40名顾客的评分的中位数记为 , 求 , 并将评分超过和不超过的顾客数填入下面的列联表:超过
不超过
男顾客
女顾客
(3)、根据(2)中的列联表,能否有90%的把握认为顾客对该商场服务质量的评分与性别有关?18. 已知数列的前项和为 , 且.(1)、求的通项公式;(2)、若 , 求数列的前项和.19. 如图:在多面体中,底面是正方形, , . 底面 . (1)、证明:平面 .(2)、求异面直线与所成角的余弦值.20. 已知椭圆的离心率为;是的左焦点,直线与相交于 , 两点,直线与的另一交点为 , 直线与的另一交点为.当时,的面积为3.(1)、求的方程;(2)、证明:直线经过定点.
(1)、证明:平面 .(2)、求异面直线与所成角的余弦值.20. 已知椭圆的离心率为;是的左焦点,直线与相交于 , 两点,直线与的另一交点为 , 直线与的另一交点为.当时,的面积为3.(1)、求的方程;(2)、证明:直线经过定点.