江西省2022届高三理数教学质量监测考试（二模）试卷

试卷更新日期：2022-04-22 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {1 ， 2 ， 3 ， 4 ， 5}$ ， $B = {x \in R | (x + 1) (x - 3) \leq 0}$ ，则集合 $A ∩ B$ 等于（）

A、{1} B、{3} C、 ${1 ， 2 ， 3}$ D、 ${3 ， 4 ， 5}$

查看试题解析
2. 已知复数 $z = \frac{a + 2 i}{i}$ （ $a \in R$ ， i是虚数单位）的虚部是-3，则复数z对应的点在复平面的（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 设m，n是不同的直线， $α$ 是平面，则下列说法正确的是（）

A、若 $m ∥ α ， m ∥ n$ ，则 $n ∥ α$ B、若 $m ∥ α ， n ∥ α$ ，则 $m ∥ n$ C、若 $m ⊥ α ， n ⊥ m$ ，则 $n ∥ α$ D、若 $m ⊥ α ， n ⊥ α$ ，则 $m ∥ n$

查看试题解析
4. 若 $θ \in [0 ， 2 π]$ ，则“ $s i n θ > 0$ ”是“ $s i n \frac{θ}{2} > 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 已知等差数列 ${a_{n}}$ 中， $a_{1} + a_{2} + a_{3} = 4$ ， $a_{13} + a_{14} + a_{15} = 12$ ，则 $a_{7} + a_{8} + a_{9}$ 等于（）

A、6 B、7 C、8 D、9

查看试题解析
6. 已知抛物线 $y^{2} = 4 x$ 的焦点为 $F$ ，圆 $E ： {(x - 4)}^{2} + {(y - m)}^{2} = 25$ 的圆心 $E$ 在抛物线上，则点 $F$ （）

A、在圆 $E$ 外 B、在圆 $E$ 上 C、在圆 $E$ 内但不与点 $E$ 重合 D、与点 $E$ 重合

查看试题解析
7. 已知命题 $p_{1}$ ：存在 $x_{0} > 0$ ，使得 $x_{0} + \frac{4}{x_{0}} \leq 4$ ，命题 $p_{2}$ ：对任意的 $x \in R$ ，都有 $t a n 2 x =$ $\frac{2 t a n x}{1 - t a n^{2} x}$ ，命题 $p_{3}$ ：存在 $x_{0} \in R$ ，使得 $3 s i n x_{0} + 4 c o s x_{0} = 6$ ，其中正确命题的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
8. 茶文化起源于中国，中国饮茶据说始于神农时代．现代研究结果显示，饮茶温度最好不要超过 $60 ℃$ ．一杯茶泡好后置于室内，1分钟、2分钟后测得这杯茶的温度分别为 $80 ℃$ ， $68 ℃$ ，给出三个茶温T（单位： $℃$ ）关于茶泡好后置于室内时间t（单位：分钟）的函数模型：① $T = a t + b (a < 0)$ ；② $T = l o g_{a} t + b (0 < a < 1)$ ；③ $T = 20 + b \cdot a^{t} (b > 0 ， 0 < a < 1)$ ．根据生活常识，从这三个函数模型中选择一个，模拟茶温T（单位： $℃$ ）关于茶泡好后置于室内时间t（单位：分钟）的关系，并依此计算该杯茶泡好后到饮用至少需要等待的时间为（参考数据 $l g 2 \approx 0.301 ， l g 3 \approx 0.477$ ）（）

A、2.72分钟 B、2.82分钟 C、2.92分钟 D、3.02分钟

查看试题解析
9. 已知函数 $f (x) = \sqrt{3} s i n 2 x - c o s 2 x$ ，若 $f (x_{1}) = - f (x_{2}) = 1$ ，且 $x_{1} ， x_{2} \in [- π ， π]$ ，则 $| x_{1} - x_{2} |$ 的最大值是（）

A、 $\frac{5 π}{6}$ B、 $\frac{7 π}{6}$ C、 $\frac{3 π}{2}$ D、 $\frac{11 π}{6}$

查看试题解析
10. 已知函数 $f (x) = {\begin{array}{l} 2^{x - 1} + 2^{1 - x} - 2 ， x \geq 0 \\ | l o g_{4} (- x) | ， x < 0 \end{array}$ ， $f (x_{1}) = f (x_{2}) = f (x_{3}) = f (x_{4})$ ，且 $x_{1} < x_{2} < x_{3} < x_{4}$ ，则 $x_{1} + x_{2} + x_{3} + x_{4}$ 的最小值是（）

A、-2 B、 $- \frac{3}{2}$ C、-1 D、 $- \frac{1}{2}$

查看试题解析
11. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点分别为 $F_{1} (- c ， 0) ， F_{2} (c ， 0)$ ，高为 $\sqrt{3} c$ 的梯形 $A F_{1} F_{2} B$ 的两顶点A，B分别在双曲线的左、右支上，且 $\vec{A F_{1}} = 4 \vec{B F_{2}}$ ，则该双曲线的离心率等于（）

A、 $\frac{6}{5}$ B、 $\frac{5}{4}$ C、 $\frac{5}{3}$ D、 $\frac{7}{3}$

查看试题解析
12. 记数列 ${3^{n - 1}}$ 中不超过正整数n的项的个数为 $a_{n}$ ，设数列 ${a_{n}}$ 的前n项的和为 $S_{n}$ ，则 $S_{3^{k}}$ $(k \in N_{+})$ 等于（）

A、 $(k - \frac{1}{3}) \cdot 3^{k} + 2 k$ B、 $(k - \frac{1}{2}) \cdot 3^{k} + k + \frac{3}{2}$ C、 $(k - \frac{3}{2}) \cdot 3^{k} + 7 k - \frac{3}{2}$ D、 $(k - \frac{3}{2}) \cdot 3^{k} + \frac{7}{2}$

查看试题解析

二、填空题

13. 已知函数 $f (x) = x s i n x + c o s x$ ，则函数 $f (x)$ 在点 $(π ， f (π))$ 处的切线方程是．

查看试题解析
14. 某单位从3男2女共5名员工中，随机抽调3名员工参加志愿服务工作，则至少有1名女员工参加的概率是．

查看试题解析
15. 设关于x，y的不等式组 ${\begin{array}{l} x + 2 y - 2 \geq 0 ， \\ 3 x - 2 y + 6 \geq 0 ， \\ 3 x + 2 y - 6 \leq 0 \end{array}$ 表示的平面区域为 $Ω$ ，若平面区域 $Ω$ 内任意点 $P (x ， y)$ ，满足 $3 x - y \geq k$ ，则实数k的取值范围是．

查看试题解析
16. 如图，在棱长为4的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点P在面 $A A_{1} B_{1} B$ 内，记 $P D ， P C$ 与平面 $D D_{1} C_{1} C$ 所成角分别为 $α ， β$ ，且 $t a n β = 3 t a n α$ ，则四棱锥 $P - A B_{1} C_{1} D$ 体积的最小值是．

查看试题解析

三、解答题

17. 如图，在四边形 $A B C D$ 中， $A B = 2$ ， $A C = \sqrt{7}$ ， $A D = 2 \sqrt{7}$ ， $∠ C A D = ∠ C B A = \frac{2 π}{3}$ ．

(1)、求 $s i n ∠ B C A$ ；

(2)、求 $B D$ ．

查看试题解析
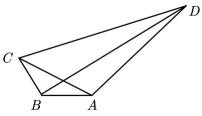18. 投资人甲为预测某行业的发展前景，对100位从事该行业的人进行了访问，根据被访问者的问卷评分（满分100分）得到如下频率分布直方图．将该行业发展前景预期分为三个等级，评分不超过40分认为悲观，大于40分不超过60分认为尚可，超过60分认为乐观．将这100人预测各等级的频率估计为未来该行业各等级发生的可能性．

(1)、估计这100个人评分的平均值和中位数；

(2)、投资人甲在该行业有A，B两个备选投资项目，投资回报率都与该行业发展前景等级有关，根据分析，大致关系如下：
行业发展前景等级
乐观
尚可
悲观
项目A年回报率（ $%$ ）
16
8
-16
项目B年回报率（ $%$ ）
13
9
-3
根据以上信息，分别计算这两个备选投资项目的年回报率的期望与方差，并用统计学的知识给甲投资建议．

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中， $P C = \sqrt{3}$ ， $P C ⊥$ 底面 $A B C D$ ， $A B C D$ 是边长为2的菱形， $∠ B A D = 60 °$ ，正 $△ A D Q$ 所在平面与底面 $A B C D$ 垂直．

(1)、求证： $P Q / /$ 平面 $A B C D$ ；

(2)、求二面角 $P - Q D - A$ 的正弦值．

查看试题解析
20. 已知两动直线 $l_{1} ： y = k (x + 2)$ ， $l_{2} ： y = k x (k \neq 0)$ 分别过椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点和中心，当 $l_{1}$ 过椭圆上顶点时，直线 $l_{1} ， l_{2}$ 的距离为 $\sqrt{2}$ ．

(1)、求椭圆C的方程；

(2)、设 $l_{1}$ 与椭圆C交于A，B两点，点A关于 $l_{2}$ 的对称点为 $A^{'}$ ，若经过点A， $A^{'}$ ， B的圆的圆心为点M，求点M横坐标的取值范围．

查看试题解析
21. 已知函数 $f (x) = a l n x + \frac{x^{2}}{2} - (a + 1) x + a + \frac{1}{2} (a \in R)$ 有一个大于1的零点 $x_{0}$ ．

(1)、求实数a的取值范围；

(2)、证明：对任意的 $x \in (1 ， x_{0}]$ ，都有 $a l n x - x + 1 > 0$ 恒成立．

查看试题解析
22. 在直角坐标系 $x O y$ 中，曲线C的参数方程为 ${\begin{array}{l} x = 3 + 3 s i n α + 4 c o s α ， \\ y = 4 s i n α - 3 c o s α \end{array}$ （ $α$ 为参数），以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l的极坐标方程为 $θ = \frac{π}{4} (ρ \in R)$ ．

(1)、求曲线C的极坐标方程；

(2)、设直线l与曲线C相交于点A，B，求 $| \frac{1}{| O A |} - \frac{1}{| O B |} |$ ．

查看试题解析
23. 已知函数 $f (x) = \sqrt{| x + 2 | + | 2 x - a | - 3 a} (a > 0)$ 的定义域为M．

(1)、若 $M = R$ ，求实数a的取值范围；

(2)、求 ${x | x \geq a} ∩ M$ ．

查看试题解析

行业发展前景等级	乐观	尚可	悲观
项目A年回报率（ $%$ ）	16	8	-16
项目B年回报率（ $%$ ）	13	9	-3