湖南省长沙市2021-2022学年八年级下学期选拨竞赛考试数学试卷

试卷更新日期：2022-04-22 类型：竞赛测试

进入出卷网下载

一、填空题

1. 满足不等式 $\frac{4}{\sqrt{2} + 1} < m < \frac{4}{3 - \sqrt{5}}$ 的整数 $m$ 的个数是.

查看试题解析
2. 已知长分别为14，13，9，7的四条线段可以构成梯形，则在所有可能构成的梯形中，连接梯形两腰中点的线段长度的最大值是.

查看试题解析
3. 如图，已知在△ABC，△ADE中，∠BAC=∠DAE=90^o ， AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE.以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE=AC+AD，其中结论正确的是（填序号）

查看试题解析
4. 已知 ${(x^{2} - x - 1)}^{x + 2} = 1$ ，则 $x =$ .

查看试题解析
5. 在平面直角坐标系内有两点A，B，其坐标为 $A (- 1 ， - 1)$ ， $B (2 ， 4)$ ，点M为x轴上的一个动点，若要使 $M B - M A$ 的值最大，则点M的坐标为.

查看试题解析
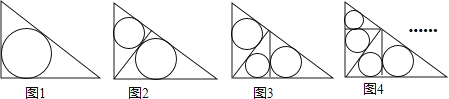
6.
如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S₁ ， S₂ ， S₃ ， …，S₁₀ ，则S₁+S₂+S₃+…+S₁₀=

查看试题解析
7. 如图，P为Rt△ABC内一点，其中∠BAC=90°，并且PA=3，PB=7，PC=9，则BC的最大值为.

查看试题解析

二、解答题

8. 已知实数a，b，c满足 $a + b + c = 0$ ， $a^{2} + b^{2} + c^{2} = 1$ ，求 $(a^{5} + b^{5} + c^{5}) \div a b c$ 的值.

查看试题解析
9. 已知： $2 {(m + 2)}^{2} + | n - 1 | = 0$ .求 $6 m^{2} n^{3} - [- 4 m n^{3} - 3 (m n - \frac{5}{3} m n^{3}) - 2 (m n + 3 m^{2} n^{3})]$ 的值.

查看试题解析
10. 如图，Rt△ABC中，AC＞BC，∠ACB=90°，CD是△ABC的中线，点E在CD上，且∠AED=∠B，求证：AE=BC.

查看试题解析
11. 某同学对矩形纸片ABCD进行了如下的操作：如图，先沿直线AG折叠，使点B落在对角线AC上的点P处，再沿直线CH折叠，使点D落在AC上的点Q处.若 $A B = 5$ ， $B C = 12$ ，求四边形 $A G C H$ 的面积.

查看试题解析
12. 已知关于x的方程 $\frac{x}{x + 1} + \frac{x + 1}{x} = \frac{4 x + a}{x (x + 1)}$ 只有一个实数根，求实数a的值.

查看试题解析
13. 设 $k$ 为非零实数，两个函数 $y = x + 2$ 与 $y = \frac{k}{x}$ 的图象相交于 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 两点，若 $| x_{1} - x_{2} | = 2 \sqrt{2}$ ，求 $k$ 的值.

查看试题解析
14. 回答下列问题：

(1)、如图，当 $∠ A B C = 90 °$ 时， $A B = B C$ ，将△PAB绕B点顺时针旋转90°画出旋转后的图形；

(2)、在（1）中，若 $P A = 2$ ， $P B = 4$ ， $P C = 6$ ，求 $∠ A P B$ 的大小.

(3)、如图， $∠ A B C = 60 °$ ， $A B = A C$ ，且 $P A = 3$ ， $P B = 4$ ， $P C = 5$ ，则△ $A P C$ 面积是.

(4)、如图，△ABC中， $∠ B A C = 60 °$ ， $A B = 2 A C$ ，点P在△ABC内，且 $P A = \sqrt{3}$ ， $P B = 5$ ， $P C = 2$ ，求△ABC的面积.

查看试题解析
15. 设 $p$ 为质数，m为整数，满足 $p^{3} + m (p - 2) = m^{2} - p + 1$ ，求 $p$ 和m的所有可取值.

查看试题解析
16. 解方程组： ${\begin{array}{l} \frac{1}{1 + x} = y \\ \frac{1}{1 + y} = z \\ \frac{1}{1 + z} = x \end{array}$ .

查看试题解析
17. 已知点M、N分别在△ABC的边AB、AC上，且不同于所在边的端点，满足 $M C = A C$ ， $N B = A B$ ，P关于直线BC的对称点为A，证明：PA是∠MPN的角平分线.

查看试题解析
18. 如图1，抛物线y＝ax²＋（a＋3）x＋3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M.

(1)、求a的值和直线AB的函数表达式；

(2)、设△PMN的周长为C₁ ， △AEN的周长为C₂ ，若 $\frac{C_{1}}{C_{2}} = \frac{6}{5}$ ，求m的值；

(3)、如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A＋ $\frac{2}{3}$ E′B的最小值.

查看试题解析