福建省青少年“大梦杯”2022年数学水平测试试卷

试卷更新日期：2022-04-22 类型：竞赛测试

进入出卷网下载

一、单选题

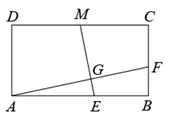
1. 已知二次函数 $y = a x^{2} + b x + c$ 的图象交x轴于A(x₁ ， 0)，B(x₂ ， 0)两点，交y轴于点C(0，3)，若 $x_{1} + x_{2} = 4$ ，且△ABC的面积为3，则a+b（）

A、3 B、-5 C、-3 D、5

查看试题解析
2. 已知实数x，y满足 $\frac{26 x^{3} y^{3}}{x^{6} - 27 y^{6}} = 1$ 且 $x^{2} \neq y^{2}$ ，则 $\frac{x^{2} + y^{2}}{x^{2} - y^{2}}$ 的值为（）

A、 $\frac{5}{4}$ B、 $\frac{4}{5}$ C、 $\frac{1}{2}$ D、2

查看试题解析
3. 将形如3m和 $2^{n}$ （m，n为正整数）的正整数从小到大排列，并依次记为 $a_{1} ， a_{2} ， a_{3} \dots$ 若第k个数 $a_{k} = 2022$ ，则k的值为（）

A、682 B、683 C、684 D、685

查看试题解析
4. 如图，在矩形ABCD中，AB=2BC，点M是CD边的中点，点E，F分别是边AB，BC上的点，且AF⊥ME，G为垂足.若EB=2，BF=1，则四边形BFGE的面积为（）

A、 $\frac{61}{52}$ B、 $\frac{85}{52}$ C、 $\frac{61}{26}$ D、 $\frac{85}{13}$

查看试题解析
5. 已知正整数a，b，c，d满足：a<b<c<d，a+b+c+d=2022， $d^{2} - c^{2} + b^{2} - a^{2} = 2022$ ，则这样的4元数组(a，b，c，d)共有（）

A、251组 B、252组 C、502组 D、504组

查看试题解析

二、填空题

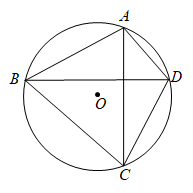
6. 若正数a，b，c满足abc=1， $a + \frac{1}{b} = 3 ， b + \frac{1}{c} = 17$ ，则 $c + \frac{1}{a} =$ .

查看试题解析
7. 如图，ABCD为圆O的内接四边形，且AC⊥BD，若AB=10，CD=8，则圆O的面积为.

查看试题解析
8. 若素数p，使得 $4 p^{2} + p + 81$ 是一个完全平方数，则p=.（若一个数能表示成某个整数的平方的形式，则称这个数为完全平方数.）

查看试题解析
9. 如果对任意的n个不大于1的非负实数 $x ，_{1} x_{2} ， x_{3} ， \dots x_{n}$ 总有 $S_{n} = {(x_{1} - x_{2})}^{2} + {(x_{2} - x_{3})}^{2} + \dots + {(x_{n - 1} - x_{n})}^{2} + {(x_{n} - x_{1})}^{2} \leq 6$ 成立，则正整数n的最大值为.

查看试题解析

三、解答题

10. 同余数是一个三边均为有理数的直角三角形的面积，即如果存在三个正有理数a，b，c，使得 $a^{2} + b^{2} = c^{2}$ ，且 $\frac{1}{2} a b = n$ ，则称n为同余数.如果正整数n为同余数，则称n为整同余数.由于5是三边长分别为 $\frac{3}{2}$ ， $\frac{20}{3}$ ， $\frac{41}{6}$ 的直角三角形的面积，6是三边长分别为3，4，5的直角三角形的面积，7是三边长分别为 $\frac{175}{60}$ ， $\frac{288}{60}$ ， $\frac{337}{60}$ 的直角三角形的面积，所以5，6，7都是同余数，且是整同余数.如何判断一个正整数是否为同余数至今尚未完全解决.关于同余数的第一个重要结论是费马（Fermat）在17世纪证明的1不是同余数.在 $a^{2} + b^{2} = c^{2}$ ， $\frac{1}{2} a b = n$ 中，令 $x = \frac{n (a + c)}{b}$ ， $y = \frac{2 n^{2} (a + c)}{b^{2}}$ ，得 $y^{2} = x^{3} - n^{2} x$ .因此，若正整数n是同余数，则二元三次不定方程 $y^{2} = x^{3} - n^{2} x$ 有有理数解；若正整数n使得二元三次不定方程 $y^{2} = x^{3} - n^{2} x$ 有有理数解，则n是同余数.这样，古老的同余数问题与现代的椭圆曲线 $y^{2} = x^{3} - n^{2} x$ 的有理点（横、纵坐标均为有理数的点）之间建立了联系.阅读上述材料，请你写出椭圆曲线 $y^{2} = x^{3} - 20^{2} x$ 上的一个有理点坐标(x，y)=.

查看试题解析
11. 已知开口向上的抛物线 $y = a x^{2} + b x + c$ 与直线：y=ax+c，y=cx+a中的每一条都至多有一个公共点.

(1)、求 $\frac{c}{a}$ 的最大值；

(2)、当 $\frac{c}{a}$ 取最大值时，设直线 $y = \frac{31}{4} a$ 交抛物线 $y = a x^{2} + b x + c$ 于A，B两点，C为抛物线的顶点，若△ABC内切圆的半径为1，求a的值.

查看试题解析
12. 如图，四边形ABCD是平行四边形，∠DAC=45°，以线段AC为直径的圆与AB和AD的延长线分别交于点E和F，过点B作AC的垂线，垂足为H.求证：E，H，F三点共线.

查看试题解析
13. 将1，2，3，…，16这16个数分成8组 $(a_{1} ， b_{1}) ， (a_{2} ， b_{2}) ， \dots ， (a_{8} ， b_{8}) ，$ 若 $| a_{1} - b_{1} | + | a_{1} - b_{1} | + \dots + | a_{1} - b_{1} | = 62$ .求 ${(a_{1} - b_{1})}^{2} + {(a_{2} - b_{2})}^{2} + \dots + {(a_{8} - b_{8})}^{2}$ 的最小值.
必要时可以利用排序不等式（又称排序原理）：设 $x_{1} \leq x_{2} \leq \dots \leq x_{n}$ ， $y_{1} \leq y_{2} \leq \dots \leq y_{n}$ 为两组实数， $z_{1} \leq z_{2} \leq \dots \leq z_{n}$ 是 $y_{1} \leq y_{2} \leq \dots \leq y_{n}$ 的任一排列，则 $x_{1} y_{n} + x_{2} y_{n - 1} + \dots x_{n} y \leq x_{1} z_{1} + x_{2} z_{2} + \dots x_{n} z_{n} \leq x_{1} y_{1} + x_{2} y_{2} + \dots x_{n} y_{n}$ .

查看试题解析
14. 已知矩形ABCD的边AB=21，BC=19，r是给定的小于1的正实数.

(1)、在矩形ABCD内任意放入114个直径为1的圆.证明：在矩形ABCD内一定还可以放入一个直径为r的圆，它和这114个圆都没有交点（也不在某个圆的内部）；

(2)、在矩形ABCD内任意放入95个单位正方形（边长为1的正方形）.证明：在矩形ABCD内一定还可以放入一个直径为r的圆，它和这95个正方形都没有交点（也不在某个正方形的内部）.

查看试题解析