浙江省金华市金东区2022年初中毕业升学适应性检测数学试卷(一模)
试卷更新日期:2022-04-22 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、-22. 不等式 的解集是( )A、 B、 C、 D、3. 如图是一个放置在水平实验台上的锥形瓶,它的俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 将一副三角板按如图所示的位置摆放在直尺上,则 的度数为( )
4. 将一副三角板按如图所示的位置摆放在直尺上,则 的度数为( )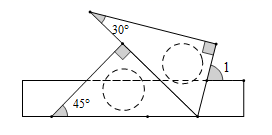 A、70° B、75° C、80° D、85°5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
A、70° B、75° C、80° D、85°5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )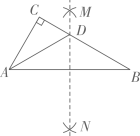 A、20° B、30° C、45° D、60°7. 已知线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为( )A、(﹣8,﹣2) B、(﹣2,﹣2) C、(2,4) D、(﹣6,﹣1)8. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A、20° B、30° C、45° D、60°7. 已知线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为( )A、(﹣8,﹣2) B、(﹣2,﹣2) C、(2,4) D、(﹣6,﹣1)8. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( ) A、
A、 B、
B、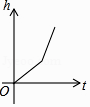 C、
C、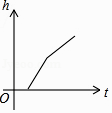 D、
D、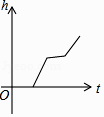 9. 函数图象如图,一元二次方程有实数根,则m最大值为( )
9. 函数图象如图,一元二次方程有实数根,则m最大值为( ) A、-3 B、-5 C、3 D、910. 已知不在同一象限的点 , 点都在函数图象上,则关于一元二次方程的两根 , 判断正确的是( )A、 B、 C、 D、的符号不确定
A、-3 B、-5 C、3 D、910. 已知不在同一象限的点 , 点都在函数图象上,则关于一元二次方程的两根 , 判断正确的是( )A、 B、 C、 D、的符号不确定二、填空题
-
11. 分解因式:.12. 函数 中,自变量x的取值范围是 .13. 一个不透明的布袋中装有分别标着数字1,2,3,4的四张卡片,现从袋中随机摸出两张卡片,则这两张卡片上的数字之和大于5的概率为.14. 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,当△ABC是直角三角形时,点C的个数为.
 15. 已知由8个边长为1的正方形组成的L型模板如图放置,其顶点E,F,G,H,I都在矩形ABCD的边上,则矩形ABCD的面积为.
15. 已知由8个边长为1的正方形组成的L型模板如图放置,其顶点E,F,G,H,I都在矩形ABCD的边上,则矩形ABCD的面积为. 16. 已知晾衣架侧面伸缩部分如图1,由6根长方形铝条(厚度忽略不计),用9个钉子A,B,C,D,E,F,G,H,I链接而成,铝条宽度都为2cm,五根较长的长为42cm,其余一根长为22cm,每个钉子都在距离长方形铝条边为1cm的地方,主视图如图2所示.晾衣架伸缩时,点B在射线AP上滑动,∠ACB的大小也随之发生变化.记铝条ACE最右侧顶点为M,铝条IH最左侧顶点为N,当时,;当时,.()
16. 已知晾衣架侧面伸缩部分如图1,由6根长方形铝条(厚度忽略不计),用9个钉子A,B,C,D,E,F,G,H,I链接而成,铝条宽度都为2cm,五根较长的长为42cm,其余一根长为22cm,每个钉子都在距离长方形铝条边为1cm的地方,主视图如图2所示.晾衣架伸缩时,点B在射线AP上滑动,∠ACB的大小也随之发生变化.记铝条ACE最右侧顶点为M,铝条IH最左侧顶点为N,当时,;当时,.()
三、解答题
-
17. 计算:.18. 先化简,再求值: , 其中.19. 某海域有A,B两个岛屿,B岛在A岛北偏西30°方向上,距A岛120海里.有一艘船从A岛出发,沿东北方向行驶一段距离后,到达位于B岛南偏东75°方向的C处.
 (1)、求∠BCA的度数.(2)、求BC的长.20. 近几年,老百姓购物的支付方式日益增多,某校数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
(1)、求∠BCA的度数.(2)、求BC的长.20. 近几年,老百姓购物的支付方式日益增多,某校数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)、本次一共调查了多少名购买者?(2)、请补全条形统计图.(3)、求在扇形统计图中A种支付方式所对应的圆心角度数.(4)、若该超市一周内有3200名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?21. 目前世界上有10亿多人以马铃薯为主粮,为国家粮食安全,丰富农民收入来源,某区试点马铃薯种植,给予每亩地每年发放150元补贴.年初,种植户金大伯根据以往经验,考虑各种因素,预计本年每亩的马铃薯销售收入为2000元,以及每亩种植成本y(元)与种植面积x(亩)之间的函数关系如图所示. (1)、根据图象,求出y与x之间的函数关系式.(2)、根据预计情况,求金大伯今年种植总收入w(元)与种植面积x(亩)之间的函数关系式.(总收入=销售收入-种植成本+种植补贴).22. 如图,已知点C在以AB为直径的半圆O上,点D为弧BC中点,连结AC并延长交BD的延长线于点E,过点E作 , 垂足为点F,交AD于点G,连结OG, , .
(1)、根据图象,求出y与x之间的函数关系式.(2)、根据预计情况,求金大伯今年种植总收入w(元)与种植面积x(亩)之间的函数关系式.(总收入=销售收入-种植成本+种植补贴).22. 如图,已知点C在以AB为直径的半圆O上,点D为弧BC中点,连结AC并延长交BD的延长线于点E,过点E作 , 垂足为点F,交AD于点G,连结OG, , . (1)、求证:.(2)、求FB的长.(3)、求OG的长.23. 定义:已知,一次函数和二次函数.若(k为实数)则y称和的“k函数”.(1)、若 , 和的“2函数”为 , 求的解析式.(2)、设一次函数和二次函数.
(1)、求证:.(2)、求FB的长.(3)、求OG的长.23. 定义:已知,一次函数和二次函数.若(k为实数)则y称和的“k函数”.(1)、若 , 和的“2函数”为 , 求的解析式.(2)、设一次函数和二次函数.①求和的“k函数”解析式(用含k的代数式表示).
②不论k取何值,和的“k函数”是否都过某定点,若是求出定点坐标;若否,请说明理由.
③不论k取何值,若二次函数上的点P关于x轴对称的点Q始终在和的“k函数”上,求点P坐标.
24. 已知在平面直角坐标系中,点 , 动点P在x轴正半轴上,作矩形OABP,点C为PB中点,△ABC沿AC折叠后得到△ADC,直线CD与矩形OABP一边交于点E. (1)、如图,当点E与原点O重合时,
(1)、如图,当点E与原点O重合时,①求证:.
②求OP长.
(2)、当 , 求点P坐标.