湖南省长沙市2021-2022学年九年级下学期期中数学试卷
试卷更新日期:2022-04-22 类型:期中考试
一、单选题
-
1. 数 , , 3.14,0中,最大的数是( )A、 B、3.14 C、 D、02. 根据国家卫健委的统计,截止4月5日清明节,我国新冠确诊病例累计超486000,用科学记数法表示这一数据是( )A、4.86×105 B、0.486×106 C、48.6×104 D、4.86×1063. 下列图形中,为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线AB∥CD, , ∠MPA=32°,则的度数是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线AB∥CD, , ∠MPA=32°,则的度数是( ) A、58° B、122° C、132° D、148°6. 如图,、为的两条弦,连接、 , 点为的延长线上一点,若∠CBD=61°,则的度数为( )
A、58° B、122° C、132° D、148°6. 如图,、为的两条弦,连接、 , 点为的延长线上一点,若∠CBD=61°,则的度数为( ) A、 B、119° C、122° D、7. 一次函数y=- 2021x+2022的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 为了解某种电动汽车一次充电后行驶的里程数,抽检了 辆车,对一次充电后行驶的里程数进行了统计,结果如图所示,则在这组数据中,众数和中位数分别是( )
A、 B、119° C、122° D、7. 一次函数y=- 2021x+2022的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 为了解某种电动汽车一次充电后行驶的里程数,抽检了 辆车,对一次充电后行驶的里程数进行了统计,结果如图所示,则在这组数据中,众数和中位数分别是( )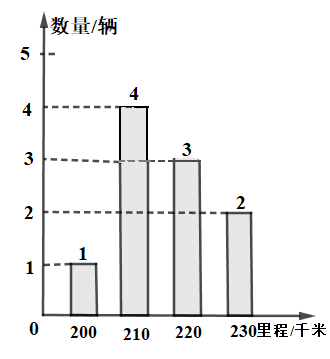 A、 B、 C、 D、9. 在一个不透明纸箱中放有除数字不同外,其它完全相同的2张卡片,分别标有数字1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之和为偶数的概率为( )A、 B、 C、 D、10. 如图,在一个由6个圆圈组成的三角形里,把-25到-30这6个连续整数分别填入图的圆圈中,要求三角形的每条边上的三个数的和都相等,那么的最小值是( )
A、 B、 C、 D、9. 在一个不透明纸箱中放有除数字不同外,其它完全相同的2张卡片,分别标有数字1、2,从中任意摸出一张,放回搅匀后再任意摸出一张,两次摸出的数字之和为偶数的概率为( )A、 B、 C、 D、10. 如图,在一个由6个圆圈组成的三角形里,把-25到-30这6个连续整数分别填入图的圆圈中,要求三角形的每条边上的三个数的和都相等,那么的最小值是( ) A、-84 B、-85 C、-86 D、-87
A、-84 B、-85 C、-86 D、-87二、填空题
-
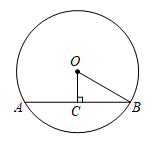
11. 分解因式:6x2y﹣3xy=.12. 如图,在中,弦的长为 , 圆心到弦的距离为6,则的度数为.
 13. 如图,在菱形中,对角线 , 相交于点 , 为中点,AC=3,BD=4,则线段的长为.
13. 如图,在菱形中,对角线 , 相交于点 , 为中点,AC=3,BD=4,则线段的长为. 14. 已知关于的一元二次方程的一个根为3,则.15. 如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为 .
14. 已知关于的一元二次方程的一个根为3,则.15. 如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD:DC=3:2,则点D到AB的距离为 . 16. 明德华兴中学自2021年下学期恢复高中办学后,街舞社按四个年级分、、、四个学习小组,小明同学根据各小组的成员人数绘制了条形统计图(1),小华同学绘制了扇形统计图(2),其中_.
16. 明德华兴中学自2021年下学期恢复高中办学后,街舞社按四个年级分、、、四个学习小组,小明同学根据各小组的成员人数绘制了条形统计图(1),小华同学绘制了扇形统计图(2),其中_.
三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中 , .19. 人教版初中数学教科书七年级下册第18-19页告诉我们平行线所具有的3个性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
其中性质2、3都是利用性质1推导出来的,但是书上却没给出性质1的推理过程,而是通过测量观察数据而得出的.九年级上册学习了反证法后,我们可以尝试给出证明了.
已知:直线AB//CD,直线EF分别交AB、CD于点G、H,求证:∠BGF=∠DHF.

证明:假设 (1),
过点G作直线PQ,使得∠PGF=∠DHF,
∴PQ//CD((2)),
∵AB//CD,且AB也过点G,
∴与((3))矛盾,
所以假设错误,即∠BGF=∠DHF.
请完成上面(1)、(2)、(3)空:
(1)、;(2)、;(3)、请选择合理的依据( )A、两点确定一条直线 B、两直线平行,同位角相等 C、经过直线外一点,有且只有一条直线与这条直线平行 D、如果两条直线都与第三条直线平行,那么这两条直线也互相平行20. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:摸球的次数
100
150
200
500
800
1000
摸到白球的次数
58
96
116
295
484
601
摸到白球的频率
0.58
0.64
0.58
0.59
0.605
0.601
(1)、请估计:当很大时,摸到白球的频率将会接近(结果保留小数点后一位),试估算口袋中白球有只;(2)、如果再加入若干个白球后,使摸到白球的概率为0.9,求加入的白球数量.21. 如图,已知点是中边的中点,连接并延长交的延长线于点 , 连接 , , 且.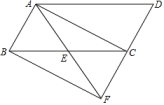 (1)、求证:四边形为矩形;(2)、若是等边三角形,且边长为 , 求四边形的面积.22. 高举“泰安球王”旗帜,发展全校篮球特色,为了落实好长沙市大课间训练,学校准备从体育用品商场一次性购买若干篮球和跳绳.每个篮球的价格都相同,每根跳绳的价格也相同.已知篮球的单价比跳绳单价的2倍少15元,用相同的费用,购买的跳绳数量与购买的篮球数量之比为.(1)、跳绳和篮球的单价各是多少元?(2)、根据学校实际情况,需一次性购买跳绳和篮球共1600个,但要求跳绳和篮球的总费用不超过57400元,学校最多可以购买多少个篮球?23. 如图,在中, , 是边上的一点,过作交于点 , , 连接交于点.
(1)、求证:四边形为矩形;(2)、若是等边三角形,且边长为 , 求四边形的面积.22. 高举“泰安球王”旗帜,发展全校篮球特色,为了落实好长沙市大课间训练,学校准备从体育用品商场一次性购买若干篮球和跳绳.每个篮球的价格都相同,每根跳绳的价格也相同.已知篮球的单价比跳绳单价的2倍少15元,用相同的费用,购买的跳绳数量与购买的篮球数量之比为.(1)、跳绳和篮球的单价各是多少元?(2)、根据学校实际情况,需一次性购买跳绳和篮球共1600个,但要求跳绳和篮球的总费用不超过57400元,学校最多可以购买多少个篮球?23. 如图,在中, , 是边上的一点,过作交于点 , , 连接交于点. (1)、求证:是的垂直平分线;(2)、若点为的中点, , 求的长.24. 俄罗斯人与乌克兰人本是同根同源的罗斯人,现在却背道而驰,正如与 , 定义:叫做函数的“罗斯函数”.比如:就是的“罗斯函数”.数形结合是学习函数的一种重要方法,对于二次函数的常数),若点在函数的图象上,则点也在其图象上,即从数的角度可以知道它的图象关于轴对称.根据上面的定义和提示,解答下列问题:
(1)、求证:是的垂直平分线;(2)、若点为的中点, , 求的长.24. 俄罗斯人与乌克兰人本是同根同源的罗斯人,现在却背道而驰,正如与 , 定义:叫做函数的“罗斯函数”.比如:就是的“罗斯函数”.数形结合是学习函数的一种重要方法,对于二次函数的常数),若点在函数的图象上,则点也在其图象上,即从数的角度可以知道它的图象关于轴对称.根据上面的定义和提示,解答下列问题: (1)、的图象的对称轴是 ;(2)、在如图所示的平面直角坐标系中画出的“罗斯函数”的大致图象;(3)、若直线与轴交于点A,与轴交于点 , 与的“罗斯函数”图象交于、两点,过点作DE⊥x轴,垂足为点 , 过点C作CF⊥x轴,垂足为点F,若△AFC与△AED的面积比为1:4,求的值.25. 已知为的外接圆, , 点是劣弧上一点(不与点 , 重合),连接 , , .
(1)、的图象的对称轴是 ;(2)、在如图所示的平面直角坐标系中画出的“罗斯函数”的大致图象;(3)、若直线与轴交于点A,与轴交于点 , 与的“罗斯函数”图象交于、两点,过点作DE⊥x轴,垂足为点 , 过点C作CF⊥x轴,垂足为点F,若△AFC与△AED的面积比为1:4,求的值.25. 已知为的外接圆, , 点是劣弧上一点(不与点 , 重合),连接 , , . (1)、如图1,若是直径,将绕点逆时针旋转得到.若 , 求四边形的面积;(2)、如图2,若 , 半径为2,设线段的长为.四边形的面积为.
(1)、如图1,若是直径,将绕点逆时针旋转得到.若 , 求四边形的面积;(2)、如图2,若 , 半径为2,设线段的长为.四边形的面积为.①求与的函数关系式;
②若点 , 分别在线段 , 上运动(不含端点),经过探究发现,点运动到每一个确定的位置.的周长有最小值 , 随着点的运动,的值会发生变化.求所有值中的最大值,并求此时四边形的面积.