江苏省扬州市邗江区第三共同体2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-04-22 类型：期中考试

进入出卷网下载

一、单选题

1. 栖霞市文明城市建设中，大力开展“垃圾分类”知识宣传活动，活动中推出下列图标（不包含文字），则其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在 $\frac{y}{4}$ ， $\frac{6}{x + y}$ ， $\frac{x^{2} - x}{x}$ ， $\frac{5 + y}{π}$ ， $\frac{4}{3} x y^{2}$ 中，分式的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列调查中，最适合采用全面调查方式的是（）

A、调查扬州市市民平均每日废弃口罩的数量 B、调查某一批次LED灯泡的使用寿命 C、调查“神舟十三号”飞船零部件的合格情况 D、调查扬州市市民进行垃圾分类的情况

查看试题解析
4. 某市有5500名学生参加考试，为了了解考试情况，从中抽取1000名学生的成绩进行统计分析，在这个问题中，有下列三种说法：①1000名考生是总体的一个样本；②5500名考生是总体；③样本容量是1000．其中正确的说法有（　　）

A、0种 B、1种 C、2种 D、3种

查看试题解析
5. 如果把 $\frac{5 x y}{x + y}$ 中的x与y都扩大为原来的5倍，那么这个代数式的值（）

A、不变 B、扩大为原来的5倍 C、缩小为原来的 $\frac{1}{5}$ D、扩大为原来的10倍

查看试题解析
6. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）

A、当AB＝BC时，它是菱形 B、当AC⊥BD时，它是菱形 C、当∠ABC＝90°时，它是矩形 D、当AC＝BD时，它是正方形

查看试题解析
7. 如图，在△ABC中，∠BAC＝102°，将△ABC绕点A按逆时针方向旋转得到 $△ A B^{'} C^{'}$ .若点 $B^{'}$ 恰好落在BC边上，且 $A B^{'} = C B^{'}$ ，则 $∠ C^{'}$ 的度数为（）

A、24° B、26° C、28° D、30°

查看试题解析
8. 如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝5，F为DE的中点.若△CEF的周长为18，则OF的长为（　　）

A、3 B、4 C、 $\frac{5}{2}$ D、 $\frac{7}{2}$

查看试题解析

二、填空题

9. 当x＝时，分式 $\frac{x - 3}{x}$ 的值为零.

查看试题解析

10. 综合实践小组的同学们在相同条件下做了测定某种黄豆种子发芽率的实验，结果如表所示：

黄豆种子数（单位：粒）

800

1000

1200

1400

1600

1800

2000

发芽种子数（单位：粒）

762

948

1142

1331

1518

1710

1902

种子发芽的频率（结果保

留至小数点后三位）

0.953

0.948

0.952

0.951

0.949

0.950

0.951

那么这种黄豆种子发芽的概率约为（精确到0.01）

查看试题解析

11. 如图，在平行四边形ABCD中，BE平分∠ABC，点E在AD上，BC=6，DE=2，则平行四边形ABCD的周长等于.

查看试题解析
12. 某班在大课间活动中抽查了10名学生每分钟跳绳次数，得到如下数据（单位：次）：88，9l，93，102，108，117，121，130，146，188．则跳绳次数在90～110这一组的频率是．

查看试题解析
13. 已知 $\frac{1}{x} - \frac{1}{y} = 5$ ，则 $\frac{2 x + 3 x y - 2 y}{x - 2 x y - y} =$ .

查看试题解析
14. 如图，四边形ACDF是正方形，∠CEA和∠ABF都是直角且点E，A，B三点共线，AB=4，则阴影部分的面积是。

查看试题解析
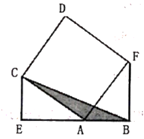15. 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．

查看试题解析
16. 如图，在四边形ABCD中，E，F，G，H分别是BC，AC，AD，BD的中点，要使四边形EFGH是菱形，四边形ABCD的边AB、CD应满足的条件是.

查看试题解析
17. 若分式方程 $\frac{x - 2}{x - 3} - 2 = \frac{m}{x - 3}$ 有增根，则m的值为.

查看试题解析
18. 如图，已知正方形 $A B C D$ 的边长为1，点 $E$ 是 $A B$ 边上一动点，连接 $E D$ ，将 $E D$ 绕点 $E$ 顺时针旋转90°到EF，连接 $D F$ 、 $C F$ ，则 $D F + C F$ 的最小值等于.

查看试题解析

三、解答题

19. 解方程

(1)、 $\frac{1}{x - 2} = \frac{1 - x}{2 - x} - 3$

(2)、 $\frac{2 x + 8}{3 x - 9} = \frac{4 x - 3}{x - 3} + 1$

查看试题解析
20. 先化简再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - x}$ ，其中x的值从0，1，2，－1中选取一个数.

查看试题解析
21. 如图，方格纸中每个小正方形的边长为1，△ABC的顶点均在格点上.根据下列要求，利用直尺画图（不写作法）：

（ 1 ）画出△ABC绕着点C按顺时针方向旋转90°后的△A₁B₁C；

（ 2 ）画出△ABC关于原点O对称的△A₂B₂C₂.

查看试题解析
22. 第24届冬季奥林匹克运动会，即2022年北京冬季奥运会，将于2022年2月4日开幕，共设7个大项，15个分项，109个小项.学校从七年级同学中随机抽取若干名，组织了奥运知识竞答活动，将他们的成绩进行整理，得到如下不完整的频数分布表、频数分布直方图与扇形统计图.（满分为100分，将抽取的成绩分成A，B，C，D四组，每组含最大值不含最小值）
分组
频数
A：60～70
4
B：70～80
12
C：80～90
16
D：90～100
△

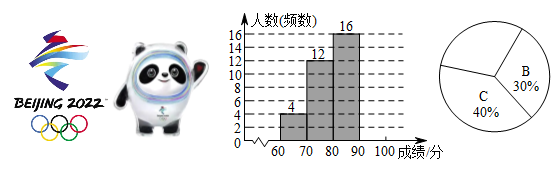(1)、本次知识竞答共抽取七年级同学名，D组成绩在扇形统计图中对应的圆心角为°；

(2)、请将频数分布直方图与扇形统计图补充完整；

(3)、学校将此次竞答活动的D组成绩记为优秀，已知该校初、高中共有学生2400名，小敏想根据七年级竞答活动的结果，估计全校学生中奥运知识掌握情况达到优秀等级的人数.请你判断她这样估计是否合理并说明理由.

查看试题解析
23. 抗击新冠肺炎疫情期间，某口罩厂接到加大生产的紧急任务后积极扩大产能，现在每天生产的口罩比原来多4万个.已知现在生产100万个口罩所需的时间与原来生产60万个口罩所需的时间相同，问口罩厂现在每天生产多少万个口罩?

查看试题解析
24. 已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE.

(1)、求证：△AFD≌△CEB.

(2)、求证：四边形ABCD是平行四边形.

查看试题解析
25. 如图，在平面直角坐标系中，四边形AOCB的点O在坐标原点上，点A在y轴上，AB∥OC，点B的坐标为（15，8），点C的坐标为（21，0），动点M从点A沿AB方向以每秒1个长度单位的速度运动，动点N从C点沿CO的方向以每秒2个长度单位的速度运动.点M、N同时出发，一点到达终点时，另一点也停止运动，设运动时间为t秒.

(1)、当t＝2时，点M的坐标为，点N的坐标为；

(2)、当t为何值时，四边形AONM是矩形？

查看试题解析
26. 如图，在▱ABCD 中，以点 A 为圆心，AB 长为半径画弧交 AD 于点 F，再分别以点 B、F 为圆心，大于 $\frac{1}{2}$ BF 的相同长为半径画弧，两弧交于点 P，连接 AP 并延长交 BC 于点 E，连接 EF.

(1)、根据以上尺规作图的过程，证明四边形 ABEF 是菱形；

(2)、若菱形 ABEF 的边长为 2，AE＝ 2 $\sqrt{3}$ ，求菱形 ABEF 的面积.

查看试题解析
27. 我们知道：分式和分数有着很多的相似点.如类比分数的基本性质，我们得到了分式的基本性质；类比分数的运算法则，我们得到了分式的运算法则，等等.小学里，把分子比分母小的分数叫做真分数.类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式.任何一个假分式都可以化作整式与真分式的和的形式.
如： $\frac{x + 1}{x - 1} = \frac{x - 1 + 2}{x - 1} = \frac{x - 1}{x - 1} + \frac{2}{x - 1} = 1 + \frac{2}{x - 1}$ ； $\frac{2 x - 3}{x + 1} = \frac{2 x + 2 - 5}{x + 1} = \frac{2 x + 2}{x + 1} + \frac{- 5}{x + 1} = 2 + (- \frac{5}{x + 1})$

(1)、下列分式中，属于真分式的是（填序号）；
① $\frac{a - 2}{a + 1}$ ② $\frac{x^{2}}{x + 1}$ ③ $\frac{a^{2} + 3}{a^{2} - 1}$ ④ $\frac{2 b}{b^{2} + 3}$

(2)、将假分式 $\frac{4 a + 3}{2 a - 1}$ 化为整式与真分式的和的形式： $\frac{4 a + 3}{2 a - 1} =$ ；若假分式 $\frac{4 a + 3}{2 a - 1}$ 的值为正整数，则整数 $a$ 的值为；

(3)、请你写出假分式 $\frac{2 a^{2} + 6}{a - 1}$ 化成整式与真分式的和的形式的完整过程.

查看试题解析
28. 问题情境：如图，在正方形ABCD中，CE⊥DF.易证：CE＝DF.（不需要写出证明过程）
问题探究：在“问题情境”的基础上请研究.

(1)、如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段AE与MN之间的数量关系，并说明理由.

(2)、如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，CQ（图中未连），判断线段EQ与CQ之间的数量关系，并说明理由.

(3)、在（2）的条件下延长EQ交边AD于点F.则∠AEF= °；

(4)、拓展提高：如图3，若该正方形ABCD边长为8，将正方形沿着直线MN翻折，使得BC的对应边B′C′恰好经过点A，过点A作AG⊥MN，垂足分别为G，若AG＝5，请直接写出AC′的长 .

查看试题解析

分组	频数
A：60～70	4
B：70～80	12
C：80～90	16
D：90～100	△