2022年浙教版数学九上复习阶梯训练：第1章二次函数（优生集训）3

试卷更新日期：2022-04-22 类型：复习试卷

进入出卷网下载

一、综合题

1. 已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”.

(1)、①如图2，求出抛物线y＝x²的“完美三角形”斜边AB的长；
②抛物线y＝x²+1与y＝x²的“完美三角形”的斜边长的数量关系是 ▲ ；

(2)、若抛物线y＝ax²+4的“完美三角形”的斜边长为4，求a的值；

(3)、若抛物线y＝mx²+2x+n﹣5的“完美三角形”斜边长为n，且y＝mx²+2x+n﹣5的最大值为﹣1，求m，n的值.

查看试题解析
2. 已知抛物线y＝mx²+（2﹣2m）x+m﹣2（m是常数）.

(1)、求证：无论m取何值，该抛物线都与x轴有两个不同的交点.

(2)、当m取不同的值时，该抛物线的顶点均在某个函数的图象上，求出这个函数的表达式.

(3)、若抛物线顶点在第四象限，当x⩽0时，至少存在一个x的值，使y＜0，求m的取值范围.

查看试题解析
3. 如图，在平面直角坐标系中，已知点A坐标为（6，8），O为坐标原点，连结OA，二次函数y＝x²图象从点O沿OA方向平移，顶点始终在线段OA上（包括端点O和A），平移后的抛物线y＝ax²+bx+c与直线x＝6交于点P，顶点为M.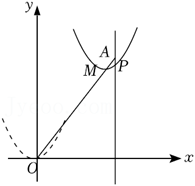

(1)、若OM＝5，求此时二次函数的解析式，并求不等式ax²+bx+c≥ $\frac{4}{3}$ x的解集.

(2)、二次函数图象平移过程中，设点M的横坐标为m，直线AP交x轴于点B，线段PB是否存在最小值？若存在，求出此时m的值；若不存在，说明理由.

查看试题解析
4. 若y是x的函数，h为常数（ $h > 0$ ），若对于该函数图象上的任意两点（ $x_{1}$ ， $y_{1}$ ）、（ $x_{2}$ ， $y_{2}$ ），当 $a \leq x_{1} \leq b$ ， $a \leq x_{2} \leq b$ （其中a、b为常数， $a < b$ ）时，总有 $| y_{1} - y_{2} | \leq h$ ，就称此函数在 $a \leq x \leq b$ 时为有界函数，其中满足条件的所有常数h的最小值，称为该函数在 $a \leq x \leq b$ 时的界高．

(1)、函数：① $y = 2 x$ ，② $y = \frac{1}{x}$ ，③ $y = x^{2}$ 在 $- 1 \leq x \leq 1$ 时为有界函数的是：（填序号）；

(2)、若一次函数 $y = k x + 2$ （ $k \neq 0$ ），当 $a \leq x \leq b$ 时为有界函数，且在此范围内的界高为 $b - a$ ，请求出此一次函数解析式；

(3)、已知函数 $y = x^{2} - 2 a x + 5$ （ $a > 1$ ），当 $1 \leq x \leq a + 1$ 时为有界函数，且此范围内的界高不大于4，求实数a的取值范围．

查看试题解析
5. 合肥市某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，销售单价 $p$ （元/千克）与时间第 $t$ （天）之间的函数关系为：
$p = {\begin{array}{l} \frac{1}{4} t + 16 (1 \leq t \leq 40 ，且 t 为整数) \\ - \frac{1}{2} t + 46 (41 \leq t \leq 80 ，且 t 为整数) \end{array}$ ，日销售量 $y$ （千克）与时间第 $t$ （天）之间的函数关系如图所示：

(1)、哪一天的日销售利润最大？最大利润是多少？

(2)、该养殖户有多少天日销售利润不低于2400元？

(3)、在实际销售的前40天中，该养殖户决定每销售1千克小龙虾，就捐赠 $m (m < 7)$ 元给村里的特困户．在这前40天中，每天扣除捐赠后的日销售利润随时间 $t$ 的增大而增大，求 $m$ 的取值范围．

查看试题解析
6. 如图，对称轴x＝1的抛物线y＝ax²+bx+c与x轴交于A（﹣2，0），B两点，与y轴交于点C（0，2），

(1)、求抛物线和直线BC的函数表达式；

(2)、若点Q是直线BC上方的抛物线上的动点，求△BQC的面积的最大值；

(3)、点P为抛物线上的一个动点，过点P作过点P作PD⊥x轴于点D，交直线BC于点E．若点P在第四象限内，当OD＝4PE时，△PBE的面积；

(4)、在（3）的条件下，若点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B，D，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，请说明理由．

查看试题解析
7. 如图，在平面直角坐标系中，抛物线 $y = - x^{2} + b x + c$ ，与 $y$ 轴交于点 $A$ 与 $x$ 轴交于点 $E$ 、 $B$ ．且点 $A (0 ， 5)$ ， $B (5 ， 0)$ ，点 $P$ 为抛物线上的一动点．

(1)、求二次函数的解析式；

(2)、如图1，过点 $A$ 作 $A C$ 平行于 $x$ 轴，交抛物线于点 $C$ ，若点 $P$ 在 $A C$ 的上方，作 $P D$ 平行于 $y$ 轴交 $A B$ 于点 $D$ ，连接 $P A$ ， $P C$ ，当 $S_{四边形 A P C D} = \frac{24}{5} S_{Δ A O E}$ 时，求点 $P$ 坐标；

(3)、设抛物线的对称轴与 $A B$ 交于点 $M$ ，点 $Q$ 在直线 $A B$ 上，当以点 $M$ 、 $E$ 、 $P$ 、 $Q$ 为顶点的四边形为平行四边形时，请直接写出点 $Q$ 的坐标．

查看试题解析
8. 二次函数y＝a(x－p)(x－q)的图象与x轴交于A ， B两点，与y轴交于C点，且A(1，0)， C(0，m)(m≥0)．

(1)、用只含a ， m的代数式表示点B的坐标．

(2)、当AB＝ $\frac{1}{2}$ 时，写出二次函数的对称轴．

(3)、若点P(n ， y₁)，Q(4，y₂)均在二次函数y＝a(x－p)(x－q)图象上，且当－2＜n＜4时，有y₁＜y₂ ，求实数的取值范围．

查看试题解析
9. 如图，已知抛物线y＝﹣x²+bx+c经过点A（﹣1，0），B（3，0），与y轴交于点C ，点P是抛物线上一动点，连接PB ， PC ．

(1)、求抛物线的解析式；

(2)、如图1，当点P在直线BC上方时，过点P作PD⊥x轴于点D ，交直线BC于点E ．若PE＝2ED ，求△PBC的面积；

(3)、抛物线上存在一点P ，使△PBC是以BC为直角边的直角三角形，求点P的坐标．

查看试题解析
10. 如图，直线 $y = - \frac{1}{2} x + 2$ 与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B、C和点A（-1，0）．

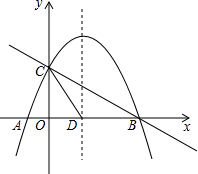(1)、求B、C两点坐标；

(2)、求该二次函数的关系式；

(3)、若抛物线的对称轴与x轴的交点为D，点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

(4)、若抛物线的对称轴与x轴的交点为D，则在抛物线在对称轴上是否存在在P，使三角形PCD是以CD为腰在等腰三角形？如果存在，直接写出点P在坐标；如果不存在，请说明理由．

查看试题解析
11. 若抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与直线 $y = m x + n (m \neq 0)$ 交 $y$ 轴于同一点，且抛物线的顶点在直线 $y = m x + n$ 上，称该抛物线与直线互为“伙伴函数”，直线的伙伴函数表达式不唯一.

(1)、求抛物线 $y = x^{2} - 2 x - 3$ 的“伙伴函数”表达式；

(2)、若直线 $y = m x - 3$ 与抛物线 $y = x^{2} - 6 x + c$ 互为“伙伴函数”，求m与c的值；

(3)、设互为“伙伴函数”的抛物线顶点坐标为 $(- k ， t)$ 且 $k t = 3$ ，它的一个“伙伴函数”表达式为 $y = 3 x + 6$ ，求该抛物线表达式，并确定在 $- 4 \leq x \leq 4$ 范围内该函数的最大值.

查看试题解析
12. 定义；若关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若函数G₁的图象与函数G₂的图象相交于A、B两点，其中一个点的横坐标等于另一点的横坐标的2倍，则称函数G₁与函数G₂互为“倍根函数”，A、B两点间的水平距离为“倍宽”.

(1)、若 $(x - 4) (2 x + k) = 0$ 是“倍根方程”，求k的值；

(2)、函数 $y = - m x$ 与 $y = x^{2} - k$ 互为“倍根函数”且“倍宽”为2，求 $m ， k$ 的值；

(3)、直线l：y＝tx+d与抛物线L：y＝2x²+px+q（q≠d）互为“倍根函数”，若直线l与抛物线L相交于A（x₁ ， y₁），B（x₂ ， y₂）两点，且2+2t²≤AB²≤3+3t² ，令6x₀＝|p﹣t|，若二次函数y₀＝﹣（x₀﹣m）²+m²+1有最大值4，求实数m的值.

查看试题解析
13. 如图，已知抛物线y＝﹣x²＋bx＋c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N.其顶点为D.

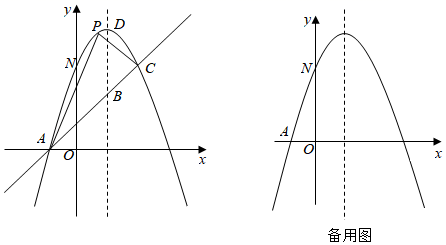(1)、抛物线及直线AC的函数关系式；

(2)、若P是抛物线上位于直线AC上方的一个动点，求 $△$ APC的面积的最大值.

(3)、在抛物线对称轴上是否存在一点M，使以A，N，M为顶点的三角形是直角三角形？若存在，请直接写出点M的坐标.若不存在，请说明理由.

查看试题解析
14. 如图1，已知抛物线y＝ax²经过点（﹣2，1）.

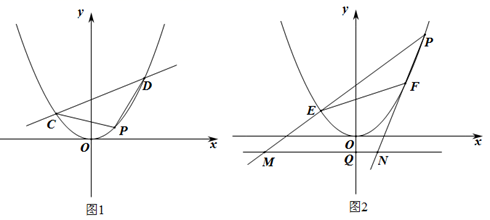(1)、求抛物线的解析式；

(2)、若直线y＝ $\frac{1}{2}$ x+2交抛物线于点C、D，点P是直线CD下方的抛物线上一动点，若S_△PCD最大，求此时点P的坐标，并求出S_△PCD的最大值；

(3)、如图2，直线y＝kx+2与抛物线交于点E，F，点P是抛物线上的动点，延长PE，PF分别交直线y＝﹣2于M，N两点，MN交y轴于Q点，求QM•QN的值.

查看试题解析
15. 如图1，已知抛物线y＝ $\frac{1}{4}$ x²与直线y＝ $- \frac{3}{4}$ x+1交于A、B两点（A在B的左侧）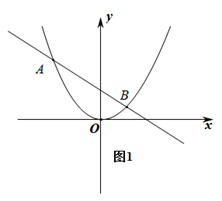

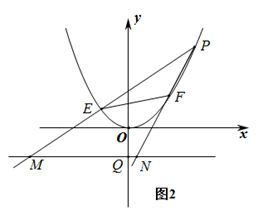(1)、求A、B两点的坐标.

(2)、在直线AB的上方的抛物线上有一点D， $S_{△ ABD} = \frac{35}{4}$ ，求点D的坐标.

(3)、如图2，直线y＝kx+2与抛物线交于点E、F，点P是抛物线上的动点，延长PE、PF分别交直线y＝﹣2于M、N两点，MN交y轴于Q点，求QM•QN的值.

查看试题解析
16. 如图，点 $A ， B$ 在函数 $y = \frac{1}{4} x^{2}$ 的图像上．已知 $A ， B$ 的横坐标分别为－2、4，直线 $A B$ 与 $y$ 轴交于点 $C$ ，连接 $O A ， O B$ ．

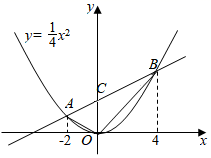(1)、求直线 $A B$ 的函数表达式；

(2)、求 $Δ A O B$ 的面积；

(3)、若函数 $y = \frac{1}{4} x^{2}$ 的图像上存在点 $P$ ，使得 $Δ P A B$ 的面积等于 $Δ A O B$ 的面积的一半，则这样的点 $P$ 共有个．

查看试题解析
17. 如图，在平面角坐标系中，已知抛物线 $y = x^{2} - 2 x - 3$ 与x轴交于点A和点B，点A在点B的左侧，与y轴交于点C.

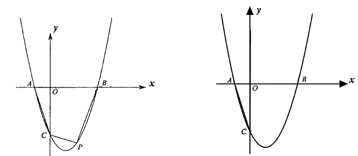(1)、求A点、C点的坐标；

(2)、点P是第四象限内的抛物线上一点，连接 $A C$ ， $C P$ ， $B P$ .若四边形 $A C P B$ 的面积为 $\frac{63}{8}$ ，请求出此时点P的坐标；

(3)、将抛物线沿射线 $A C$ 方向平移 $\sqrt{10}$ 个单位长度得到新抛物线 $y^{'}$ ，新抛物线 $y^{'}$ 与原抛物线对称轴交于点D.点E为新抛物线 $y^{'}$ 上的一个动点，点 $F$ 为直线 $B C$ 上一点，直接写出所有使得以点D，E，F，B为顶点构成的四边形是平行四边形的点E的横坐标，并把求其中一个点E的横坐标的过程写出来.

查看试题解析
18. 已知函数y＝﹣x²+（m﹣1）x+m（m为常数），其顶点为M.

(1)、请判断该函数的图象与x轴公共点的个数，并说明理由；

(2)、当﹣2≤m≤3时，求该函数的图象的顶点M纵坐标的取值范围；

(3)、在同一坐标系内两点A（﹣1，﹣1）、B（1，0），△ABM的面积为S，当m为何值时，S的面积最小？并求出这个最小值.

查看试题解析
19. 已知：二次函数y=x²+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．

(1)、求抛物线的解析式；

(2)、抛物线的对称轴上有一动点P，求出PA+PD的最小值；

(3)、点G抛物线上的动点，在x轴上是否存在点E，使B、D、E、G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的E点坐标；如果不存在，请说明理由．

查看试题解析
20. 在矩形ABCD中，AB＝5cm，BC＝6cm，点P从点A开始沿边AB向终点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向终点C以2cm/s的速度移动．如果P、Q分别从A、B同时出发，当点Q运动到点C时，两点停止运动．设运动时间为t秒．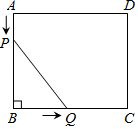

(1)、填空：BQ＝， PB＝（用含t的代数式表示）；

(2)、当t为何值时，PQ的长度等于5cm？

(3)、是否存在t的值，使得五边形APQCD的面积等于26cm²？若存在，请求出此时t的值；若不存在，请说明理由．

(4)、是否存在t的值，使△BPQ的面积最大，若存在，请直接写出此时t的值；若不存在，请说明理由．

查看试题解析
21. 如图1，在平面直角坐标系中，抛物线y＝ax²+bx+c与x轴交于点A（3，0），B（﹣1，0）两点，与y轴交于C点，且OC＝3OB，顶点为D点，连接OD.

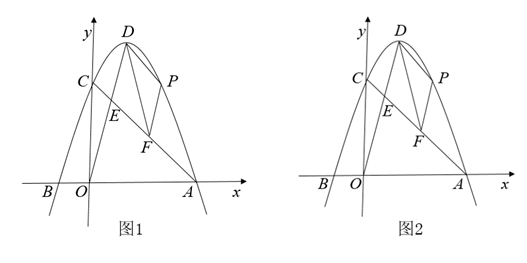(1)、求抛物线解析式；

(2)、P点为抛物线上AD部分上一动点，过P点作PF∥DE交AC于F点，求四边形DPAF面积的最大值及此时P点坐标.

查看试题解析
22. 已知二次函数y＝x²﹣2（m+1）x+3﹣m，其中m是常数.

(1)、若函数的图象经过点（﹣1，8），求此函数的解析式.

(2)、当x≤2时，y随x的增大而减小，求m的最小值.

(3)、当﹣1≤x≤2时，若二次函数图象始终在直线y＝3的上方，请直接写出m的取值范围.

查看试题解析
23. 如图，已知抛物线 $y = a x^{2} + b x + 4$ 与x轴交于 $A (- 2 ， 0)$ 、B两点，与y轴交于C点，其对称轴为直线 $x = 1$ .

(1)、直接写出抛物线的解析式；

(2)、把线段 $A C$ 沿x轴向右平移，设平移后A、C的对应点分别为 $A^{'}$ 、 $C^{'}$ ，当 $C^{'}$ 落在抛物线上时，求 $A^{'}$ 、 $C^{'}$ 的坐标；

(3)、除（2）中的平行四边形 $A C C^{'} A^{'}$ 外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形？若存在，求出E、F的坐标；若不存在，请说明理由.

查看试题解析
24. 若函数图象关于y轴对称，则我们称这样的函数为“YY函数”，例如： $y = | x |$ 是“YY函数”.

(1)、在下面的函数中，是“YY函数”的是.
① $y = 3 x$ ； ② $y = x^{2} - 5$ ； ③ $y = {\begin{array}{l} x^{2} - 2 x - 3 ， x > 0 \\ x^{2} + 2 x - 3 ， x \leq 0 \end{array}$ .

(2)、关于x的“YY函数”，当x>0的时，图象是经过A（1，2），B（3，5）的直线，当 x＜0 时，求“YY函数”的解析式.

(3)、直线 $y = a x - 2 a + 1$ 与关于x的“YY函数” $y = a x^{2} - 2 | x | + 1$ 的图象有3个交点，求a的值.

查看试题解析
25. 如图，抛物线y＝－x²＋（m－1）x＋m与y轴交于点（0，3）

(1)、当x满足时，y的值随x值的增大而减小；

(2)、当x满足0≤x≤4时，y的取值范围是；

(3)、点P为抛物线上一点，且S_△APC＝ $\frac{35}{8}$ ，求点P的坐标.

查看试题解析

2022年浙教版数学九上复习阶梯训练：第1章 二次函数 （优生集训）3

一、综合题

2022年浙教版数学九上复习阶梯训练：第1章二次函数（优生集训）3