2022年浙教版数学九上复习阶梯训练：第1章 二次函数 （优生集训）2

试卷更新日期：2022-04-22 类型：复习试卷

进入 出卷网 下载

一、综合题

  • 1. 如图，直线AB与抛物线y=12x2+bx+c交于A(−4 ， 0)、B(2 ， 6)两点，与y轴交于点C，点D为线段AB上一点，连接OD、OB.

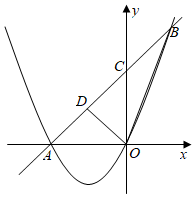    (1)、求抛物线的解析式；
    (2)、若OD将△AOB分成面积相等的两部分，求点D的坐标；
    (3)、在平面坐标内是否存在点P，使得以A、O、B、P为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.

    查看试题解析

  • 2. 如图所示，抛物线y=2x2−4x−6与x轴相交于A、B两点，与y轴相交于点C，点M为抛物线的顶点.

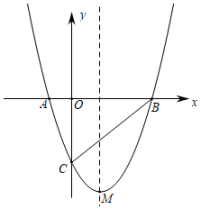    (1)、求点C及顶点M的坐标；
    (2)、在抛物线的对称轴上找一点P，使得PA+PC的值最小，请求出点P的坐标并求出最小值；
    (3)、若点N是第四象限内抛物线上的一个动点，连接BN、CN，求△BCN面积的最大值及此时点N的坐标.

    查看试题解析

  • 3. 某地实施产业扶贫种植某种水果，其成本经过测算为20元/kg ， 投放市场后，经过市场调研发现，这种水果在上市的一段时间内的销售单价p（元/kg）与时间t（天）之间的函数图象如图，且其日销售量y（kg）与时间t（天）的关系是：y=−2t+160 ， 天数为整数.

    (1)、试求销售单价p（元/kg）与时间t（天）之间的函数关系式；
    (2)、哪一天的销售利润最大？最大日销售利润为多少？
    (3)、在实际销售的前28天中，公司决定每销售1kg水果就捐赠n元利润（n<6）给“精准扶贫”对象.现发现：在前28天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围.

    查看试题解析

  • 4. 在直角坐标系中，二次函数y=ax2−bx+1（a，b是常数，a≠0）的图象经过(1 ， 1)和(2 ， 3)两点.
    (1)、求函数的表达式，并写出函数图象的顶点坐标；
    (2)、当−1<x<1时，求y的取值范围；
    (3)、当x=m ， n（m，n是实数，m≠n）时，该函数对应的函数值分别为M，N.若m+n=2 ， 求证：M+N>2.

    查看试题解析

  • 5. 某企业决定从甲、乙两种产品中选择一种生产，打入国际市场，已知生产销售这两种产品的有关数据如表：（单位：万元）


    年固定成本

    每件产品成本

    每件产品销售价

    甲产品

    20

    a

    10

    乙产品

    40

    8

    18

    a为常数，且3≤a≤8.甲产品每年最多可生产销售200件，乙产品每年最多可生产销售80件，销售乙产品x件时需另外上交0.05x2万元的特别关税.

    (1)、写出该企业生产销售乙产品的年利润y关于x的函数表达式为.
    (2)、当销售乙产品多少件时，可获乙产品的利润最大？最大利润是多少？
    (3)、该企业选择哪一种产品生产销售可获得最大年利润？请说明理由.

    查看试题解析

  • 6. 已知抛物线y＝ax2+bx+c的图象开口向下，经过点A（﹣1，0），B（3，0），与y轴交于点C，顶点为D，△ABD的面积为8.
    (1)、求抛物线的解析式.
    (2)、若在抛物线上有动点P，使得△PBC的内心恰好落在x轴上，求点P的坐标.
    (3)、将抛物线向右平移t个单位，所得抛物线与原抛物线交于点Q，顶点变为E，记△QDE的面积为S，求 st3 的值.

    查看试题解析

  • 7. 如图，抛物线y=ax2+bx−6交x轴于A(−2 ， 0) ， B(6 ， 0)两点，交y轴于点C(0 ， −6) ， 点Q为线段BC上的动点.

    (1)、求抛物线的解析式；
    (2)、求QA+QO的最小值；
    (3)、过点Q作QP∥AC交抛物线的第四象限部分于点P，连接PA ， PB ， 记△PAQ与△PBQ的面积分别为S1 ， S2 ， 设S=S1+S2 ， 当S最大时，求点P的坐标，并求S的最大值.

    查看试题解析

  • 8. 如图1，抛物线G：y＝﹣14x2+bx+c经过点B(6，0)，顶点为A，对称轴为直线x＝2.

    (1)、求抛物线G的解析式；
    (2)、若点C为直线AB上方的抛物线上的动点，当△ABC面积最大时，求C点的坐标；
    (3)、如图2，将抛物线G向左平移至顶点在y轴上，平移后的抛物线G与x轴交于点E、F，平行于x轴的直线l经过点(0，8)，若点P为x轴上方的抛物线G上的动点，分别连接EP、FP，并延长交直线l于M、N两点，若M、N两点的横坐标分别为m、n，试探究m、n之间的数量关系.

    查看试题解析

  • 9. 投影线垂直于投影面产生的投影叫做正投影”，选自《九年级下册教材》P89，粹园的同学们学完此节内容后，开始探究正投影在平面直角坐标系的应用.若平面直角坐标系中，规定曲线AB在坐标轴上的正投影的长度称为在该轴上的“影长”， 记为“l”.AB两点在对应坐标轴上的正投影之间的范围称为在该轴上的“影长范围”，例如：如图，曲线AB，其中A（ −3 ，1）、B（1，3），则曲线AB在x轴上的的“影长”l为4，在x轴上的“影长范围”为 −3≤x≤1 .

    (1)、已知反比例函数 y=−3x 的部分图象在y轴上的“影长范围”是 1≤y≤3 ，求其在x轴上的“影长”以及“影长范围”.
    (2)、若二次函数 y=−x2+ax+2a 的部分图象在x轴上的“影长范围”是 −4≤x≤2 ，且在y轴上的“影长范围”的最大值为10，求满足条件的a的值.
    (3)、已知二次函数 y=ax2+bx+c 与一次函数 y=−bx−2c 交于A、B两点，当 a+b+c=0 ，且实数 a>2b>3c ，求线段AB在x轴上的“影长”的取值范围.

    查看试题解析

  • 10. 如图，抛物线y＝ax2+2x+c经过点A（0，3），B（﹣1，0），请回答下列问题：

    (1)、求抛物线的解析式；
    (2)、抛物线的顶点为D，对称轴与x轴交于点E，连接BD，求BD的长．
    (3)、在抛物线的对称轴上是否存在点M，使得△MBC的面积是4？若存在请求出点M的坐标；若不存在请说明不存在的理由．

    查看试题解析

  • 11. 如图，直线y＝ 12 x－1与抛物线y＝ax2＋ 72 x＋c交于点A、B两点，点A在y轴上，点B的横坐标为6，过点B作BC⊥x轴，垂足为点C.

    (1)、求此抛物线的表达式；
    (2)、若直线PQ∥y轴， 与抛物线、直线AB、x轴分别交于点P、Q、D，且点D位于线段OC之间，求线段PQ长度的最大值；
    (3)、连接BP、CQ，当四边形PQCB是平行四边形时，求点D的坐标.

    查看试题解析

  • 12. 已知抛物线 y=x2+bx+c 经过 (−2 ， t)、B(3 ， t) 两点.
    (1)、求b的值；
    (2)、当 −2<x<2 时，抛物线与x轴有且只有一个公共点，求c的取值范围；
    (3)、若方程 x2+bx+c=0 的两实根 x1、x2 ，满足 1<x1−x2≤5 ，且 P=x12+2x22 ，求P的最大值.

    查看试题解析

  • 13. 在平面直角坐标系 xOy 中，抛物线 y=ax2+bx−1a 与 y 轴交于点 A ，将点 A 向右平移 2 个单位长度，得到点 B ，点 B 在抛物线上。
    (1)、求点 B 的坐标 ( 用含 a 的式子表示 ) ；
    (2)、求抛物线的对称轴；
    (3)、已知点P( 12 ， −1a  )， Q(2 ， 2) ，若抛物线与线段 PQ 恰有一个公共点，结合函数图象，求 a 的取值范围．

    查看试题解析

  • 14. 如图，已知抛物线y＝ax2+bx+3经过点A（﹣1，0）、B（3，0）两点，且交y轴交于点 C．

    (1)、求抛物线的解析式；
    (2)、点M是线段BC上的点（不与 B、C重合），过M作MN∥y轴交抛物线于N，若点M的横坐标为m，请用m的代数式表示MN的长；
    (3)、在（2）的条件下，连接NB，NC，是否存在点M，使△BNC的面积最大？若存在，求m的值及△BNC的面积最大值；若不存在，说明理由．

    查看试题解析

  • 15. 如图，抛物线 y=−12x2+bx+c 与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）.

    (1)、求抛物线的解析式；
    (2)、点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，求出线段EF的最大值及此时E点的坐标；
    (3)、在x轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由.

    查看试题解析

  • 16. 如图，二次函数y＝-x2+（k-1）x+3的图象与x轴的负半轴交于点A，与y轴交于点B，且OA＝OB．

    (1)、求该二次函数的解析式；
    (2)、若点C是二次函数图象上的一个动点，且位于第二象限；设△ABC的面积为S，试求出S的最大值．

    查看试题解析

  • 17. 如图，在平面直角坐标系中，抛物线 y=ax2+4x+c 与y轴交于点 A(0 ， 5) ，与x轴交于点 E ， B ，点B坐标为 (5 ， 0) ．

    (1)、求二次函数解析式及顶点坐标；
    (2)、过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点 ( 点P在AC上方 ) ，作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积．

    查看试题解析

  • 18. 如图，抛物线y＝ax2+bx+c与x轴的两个交点为A、B，且当x＜﹣1时，y随x的增大而减小，x＞﹣1时，y随x的增大而增大，其最小值为﹣ 125 ，其图象与x轴的交点B的横坐标是1，过点B的直线l：y＝kx+ 35 分别与y轴及抛物线交于点C，D．

    (1)、求直线l和抛物线的解析式；
    (2)、过点D作x轴的平行线交抛物线于点E，点P是直线DE上的一个动点，点D关于直线OP的对称点F恰好在y轴上，求直线OP的解析式．
    (3)、将（1）中的二次函数图象x轴下方的部分沿x轴翻折到x轴上方图象的其余部分保持不变，翻折后的图象与原图象x轴上方的部分组成一个“W”形状的新图象，将直线平移得到直线l，若直线l与该新图象恰好有三个公共点，请求出上下平移了几个单位长度．

    查看试题解析

  • 19. 如图，已知抛物线y=-x2+bx+c经过点A(-1，0)，B(3，0)，与y轴交于点C，点P是抛物线上一动点，连接PB，PC．

    (1)、求抛物线的解析式
    (2)、如图1，当点P在直线BC上方时，过点P作PD⊥x轴于点D，交直线BC于点E。若PE=2ED，求△PBC的面积
    (3)、抛物线上存在一点P，使△PBC是以BC为直角边的直角三角形，求点P的坐标．

    查看试题解析

  • 20. 已知一元二次方程x2－4x＋3=0的两根是m，n且m＜n.如图，若抛物线y=-x2+bx

    +c的图像经过点A（m，0）、B（0，n）.

    (1)、求抛物线的解析式.
    (2)、若（1）中的抛物线与x轴的另一个交点为C．根据图像回答，当x取何值时，抛物线的图像在直线BC的上方？
    (3)、点P在线段OC上，作PE⊥x轴与抛物线交于点E，若直线BC将△CPE的面积分成相等的两部分，求点P的坐标.

    查看试题解析

  • 21. 已知抛物线 y=−x2+bx+c （b，c为常数）经过点 A(0 ， 3) ， B(−1 ， 0) .
    (1)、求抛物线的解析式及对称轴；
    (2)、在平面直角坐标系xOy中，当m，n满足 m+n=mn 时，就称点 M(m ， mn) 为“美好点”.若点P、Q（P在Q左边）为抛物线上的“美好点”，点N为抛物线上P、Q之间的一点（包含P、Q），求点N的横坐标 xN 及纵坐标 yN 的取值范围.

    查看试题解析

  • 22. 如图，直线y=-x+3与x轴，y轴分别交于B，C两点，抛物线y=-x2+bx+c经过B，C两点，点A是抛物线与x轴的另一个交点

     

    (1)、求此抛物线的函数解析式；
    (2)、在抛物线上是否存在点P，使S△PAB =2S△CAB ， 若存在，求出P点的坐标；若不存在，请说明理由．

    查看试题解析

  • 23. 如图所示，已知抛物线在坐标系中的顶点为 A ，且与坐标轴交点为 B ， C 点.（相关数据见图中标示）

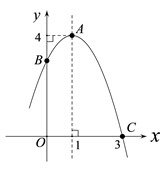    (1)、求该抛物线的解析式；
    (2)、求△ ABC 的面积；
    (3)、在 y 轴上求作一点 D 使△ ADC 得周长最小，求出满足条件的点 D 的坐标.

    查看试题解析

  • 24. 如图，在平面直角坐标系中，直线y= -x-2与抛物线y=x2-2mx+n相交于A、B两个不同的点，其中点A在x轴上.

    (1)、n=（用含m的代数式表示）
    (2)、若点B为该抛物线的顶点，分别求出m和n的值；
    (3)、若-3≤x≤0时，二次函数y=x2-2mx+n的最小值为-4，求m的值.

    查看试题解析

  • 25. 如图，在平面直角坐标系xOy中，已知抛物线y=-x2+kx-2k(k<0)与x轴正半轴交于点C，与y轴的交点为A．

    (1)、若抛物线经过点B(-3，1)，求抛物线的解析式；
    (2)、无论k取何值，抛物线都经过定点M，求点M的坐标；
    (3)、在(1)的条件下，点P是抛物线上的一个动点，记△ABP的面积为S1 ， △ABM的面积为S2 ， 设S2=nS1 ， 若符合条件的点P有三个，求n的值．

    查看试题解析