2022年浙教版数学九上复习阶梯训练：第1章二次函数（优生集训）1

试卷更新日期：2022-04-22 类型：复习试卷

进入出卷网下载

一、综合题

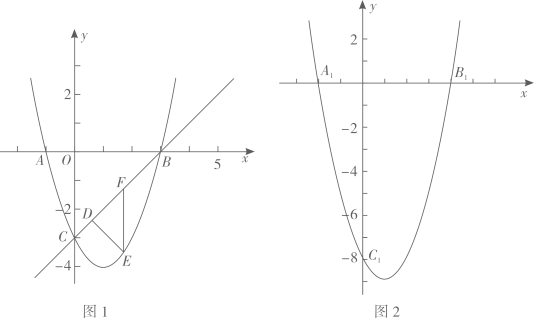
1. 如图1，在平面直角坐标系中，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于 $A$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，已知 $A (- 1 ， 0)$ ，直线 $B C$ 的解析式为 $y = x - 3$ .

(1)、求抛物线的解析式；

(2)、在线段 $B C$ 上有一动点 $D$ ，过点 $D$ 作 $D E ⊥ B C$ 交抛物线于点 $E$ ，过点 $E$ 作 $y$ 轴的平行线交 $B C$ 于点 $F$ .求 $E F - \frac{\sqrt{2}}{2} D E$ 的最大值，以及此时点 $E$ 的坐标；

(3)、如图2，将该抛物线沿 $y$ 轴向下平移5个单位长度，平移后的抛物线与坐标轴的交点分别为 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 在平面内找一点 $M$ ，使得以 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ， $M$ 为顶点的四边形为平行四边形，直接写出点 $M$ 的坐标.

查看试题解析
2. 在平面直角坐标系中，将一点（横坐标与纵坐标不相等）横坐标与纵坐标互换后得到的点叫这一点的“H点”，如（2，-3）与（-3，2）是一对“H点”.

(1)、点 $(m ， n)$ 和它的“H点”均在直线 $y = k x + a$ 上，求k的值；

(2)、若直线 $y = k x + 3$ 经过的A，B两点恰好是一对“H点”，其中点A还在反比例函数 $y = \frac{2}{x}$ 的图象上，一条抛物线 $y = x^{2} + b x + c$ 也经过A，B两点，求该抛物线的解析式；

(3)、已知 $A (m ， n) (m < n)$ ，B为抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 上的一对“H点”，且满足： $m + n = 2$ ， $m n = - 3$ ，点P为抛物线上一动点，若该抛物线上有且仅存在3个点P满足△PAB的面积为16，求 $a + b + c$ 的值.

查看试题解析
3. 平面直角坐标系中，抛物线y = - $x^{2}$ +2ax + 1 - a(a为常数)的顶点为A.

(1)、当抛物线经过点(1，2)，求抛物线的函数表达式；

(2)、求顶点A的坐标(用含字母ɑ的代数式表示)，判断顶点A在x轴的上方还是下方，并说明理由；

(3)、当x ≥0时，抛物线y = - $x^{2}$ + 2ɑx + 1 - ɑ(ɑ为常数)的最高点到直线y = 3ɑ的距离为5，求ɑ的值.

查看试题解析
4. 如图，在矩形ABCD中，AB=5，BC=4，点E是AB上一点，CE=1，点F是线段AB上一个动点，以EF为斜边向上作等腰直角三角形.

(1)、当BF=5时，求BG的长度．

(2)、点F从点B运动到点A的过程中，求AG的最小值．

查看试题解析
5. 已知，在平面直角坐标系中，抛物线 $y = x^{2} － 2 m x + m^{2} + 2 m － 1$ 的顶点为A，点B的坐标为（3 ， 5）.

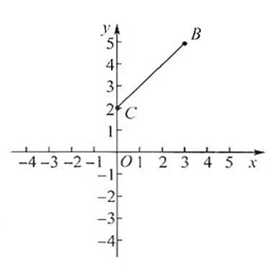(1)、求抛物线过点B时顶点A的坐标；

(2)、点A的坐标记为（ $x$ ， $y$ ），求 $y$ 关于 $x$ 的函数表达式；

(3)、已知C点的坐标为（0， 2），当m取何值时，抛物线 $y = x^{2} － 2 m x + m^{2} + 2 m － 1$ 与线段BC只有一个交点.

查看试题解析
6. 某商店购进一批清洁剂，每瓶进价为20元，出于营销考虑，要求每瓶清洁剂的售价不低于20元且不高于28元，在销售过程中发现该清洁剂每周的销售量 $y$ （瓶）与每瓶清洁剂的售价 $x$ （元）之间满足一次函数关系：当销售单价为22元时，销售量为36瓶；当销售单价为24元时，销售量为32瓶．

(1)、求出 $y$ 与 $x$ 的函数关系式，并写出 $x$ 的取值范围；

(2)、设该商店每周销售这种清洁剂所获得的利润为 $w$ 元，将该清洁剂销售单价定为多少元时，才能使商店销售该清洁剂所获利润最大？最大利润是多少？

查看试题解析
7. 如图，二次函数y＝x2＋bx＋c的图象与x轴交于A，B两点，与y轴交于点C，且关于直线x＝1对称，点A的坐标为（-1，0）．

(1)、求二次函数的表达式；

(2)、当y＜0时，写出x的取值范围；

(3)、当a≤x≤a＋1时，二次函数y＝x²＋bx＋c的最小值为2a，求a的值．

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，点A是抛物线 $y = - x^{2} + 2 m x - m^{2} - 2 m + 1$ 的顶点.

(1)、求点A的坐标（用含m的代数式表示）；

(2)、若射线 $O A$ 与x轴所成的锐角为 $45 °$ ，求m的值；

(3)、将点 $P (0 ， 1)$ 向左平移 $4$ 个单位得到点Q，若抛物线与线段 $P Q$ 只有一个公共点，直接写出m的取值范围.

查看试题解析
9. 如图1，在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x$ 经过点 $(- 2 ， 5)$ ，且与直线 $y = - \frac{1}{2} x$ 在第二象限交于点A，过点A作 $A B ⊥ x$ 轴，垂足为点 $B (- 4 ， 0)$ .若P是直线 $O A$ 上方该抛物线上的一个动点，过点P作 $P C ⊥ x$ 轴于点C，交 $O A$ 于点D，连接 $O P$ ， $P A$ .

(1)、求抛物线的解析式；

(2)、求 $△ A O P$ 的面积S的最大值；

(3)、连接 $P B$ 交 $O A$ 于点E，如图2，线段 $P B$ 与 $A D$ 能否互相平分？若能，请求出点E的坐标；若不能，请说明理由.

查看试题解析
10. 如图，在平面直角坐标系中，二次函数y＝﹣x²＋bx＋c的图象与坐标轴交于A，B，C三点，其中点B的坐标为（1，0），点C的坐标为（0，4），点D的坐标为（0，2），点P为二次函数图象上的动点.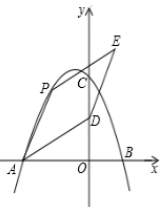

(1)、求二次函数的解析式和直线AD的解析式；

(2)、当点P位于第二象限内二次函数的图象上时，连接AD，AP，以AD，AP为邻边作平行四边形APED，设平行四边形APED的面积为S，求S的最大值.

查看试题解析
11. “三高四新”战略是习近平总书记来湘考察时，为建设现代化新湖南擘画的宏伟战略蓝图.在数学上，我们不妨约定：在平面直角坐标系中，将点 $P (3 ， 4)$ 称为“三高四新”点，经过 $P (3 ， 4)$ 的函数，称为“三高四新”函数.

(1)、下列函数是“三高四新”函数的有；
① $y = 2 x - 2$ ② $y = x^{2} - 6 x + 13$ ③ $y = - 3 x^{2} + 6 x + 11$ ④ $y = \frac{12}{x}$

(2)、若关于x的一次函数 $y = k x + b$ 是“三高四新”函数，且它与y轴的交点在y轴的正半轴，求k的取值范围；

(3)、关于x的二次函数 $y = \frac{1}{4} {(x - 3)}^{2}$ 的图象顶点为A，点 $M (x_{1} ， y_{1})$ 和点 $N (x_{2} ， y_{2})$ 是该二次函数图象上的点且使得 $∠ M A N = 90 °$ ，试判断直线MN是否为“三高四新”函数，并说明理由.

查看试题解析
12. 在平面直角坐标系中，若直线 $l ： y = k x + b (k \neq 0)$ 与函数G的图象有且只有一个交点P.则称该直线l是函数G关于点P的“联络直线”，点P称为“联络点”.

(1)、直线 $y = - x + 1$ 是函数 $y = \frac{1}{x}$ 的“联络直线”吗？请说明理由；

(2)、已知函数 $y = \frac{12}{x}$ ，求该函数关于“联络点” $(3 ， 4)$ 的“联络直线”的解析式；

(3)、若关于x的函数 $y = a x^{2} - 2 a x - 3 a (a > 0)$ 图象与x轴交于A、B两点，与y轴交于点C，点P是y轴上一点，分别过点P作函数 $y = a x^{2} - 2 a x - 3 a$ 关于点M，N的“联络直线”PM、PN.若直线 $y = k x - 1$ 恰好经过M、N两点，请用含a的式子表示线段PC的长.

查看试题解析
13. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3$ 过点 $A (- 3 ， 0)$ ， $B (1 ， 0)$ ，与y轴交于点C，连接BC，点N是第一象限抛物线上一点，连接NA，交y轴于点E， $∠ N A B = ∠ B C O$ ．

(1)、求抛物线的解析式；

(2)、求线段AN的长；

(3)、若点M在第三象限抛物线上，连接MN， $∠ A N M = 45 °$ ，则这时点M的坐标为（直接写出结果）．

查看试题解析
14. 二次函数y＝ax²+bx+4（a≠0）的图象经过点A（－4，0），B（1，0），与y轴交于点C，点P为第二象限内抛物线上一点，连接BP、AC，过点P作PD⊥x轴于点D．

(1)、求二次函数的表达式；

(2)、连接PA，PC，求 $S_{Δ P A C}$ 的最大值；

(3)、连接BC，当∠DPB＝2∠BCO时，求直线BP的表达式．

查看试题解析
15. 如图，已知二次函数 $y = {ax}^{2} + \frac{3}{2} x + 3 (a < 0)$ 的图象与x轴交于点A，B（点A在点B的左边），与y轴交于点C. 点P，Q为抛物线上两动点.

(1)、若点P坐标为（1，3），求抛物线的表达式；

(2)、如图①连结BC，在（1）的条件下，是否存在点Q，使得∠BCQ=∠ABC. 若存在，请求出点Q的坐标，若不存在，请说明理由；

(3)、若点P为抛物线顶点，连结OP，当 a 的值从-3变化到-1的过程中，求线段OP扫过的面积.

查看试题解析
16. 二次函数y₁＝ax²+2x过点A（﹣2，0）和点B，过点A，B作一次函数y₂＝kx+b，若点B的横坐标为1．

(1)、求出二次函数与一次函数的解析式；

(2)、根据图象，当y₂＞y₁时，请直接写出x的取值范围；

(3)、若P点在抛物线y₁上，且横坐标为﹣1，求△ABP的面积．

查看试题解析
17. 某公司销售一种商品，成本为每件30元，经过市场调查发现，该商品的日销售量 $y$ （件）与销售单价 $x$ （元）是一次函数关系，其销售单价、日销售量的三组对应数值如下表：
销售单价 $x$ （元）
40
60
80
日销售量 $y$ （件）
80
60
40

(1)、求公司销售该商品获得的最大日利润；

(2)、销售一段时间以后，由于某种原因，该商品每件成本增加了10元，若物价部门规定该商品销售单价不能超过 $a$ 元，在日销售量 $y$ （件）与销售单价 $x$ （元）保持（1）中函数关系不变的情况下，该商品的日销售最大利润是1500元，求 $a$ 的值．

查看试题解析
18. 已知二次函数y=ax²+bx (a≠0)的图象经过点A(2，4)，B(4，0) .

(1)、求这个二次函数的表达式.

(2)、将x轴上的点P先向上平移3n (n>0）个单位得点P，再向左平移2n个单位得点₂ ，若点P₁ ， P₂均在该二次函数图象上，求n的值.

查看试题解析
19. 已知抛物线 $G ： y = - m x^{2} + 2 m x - 3$ 有最高点．

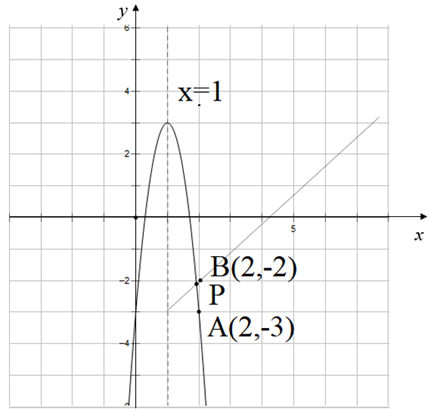(1)、m0（填“>、=、<”）；

(2)、求二次函数 $y = - m x^{2} + 2 m x - 3$ 的最大值（用含m的式子表示）；

(3)、将抛物线G向右平移m个单位得到抛物线 $G_{1}$ ．经过探究发现，随着m的变化，抛物线 $G_{1}$ 顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；

(4)、记（3）所求的函数为H，抛物线G与函数H的图象交于点P，结合图象，求点P的纵坐标 $y_{P}$ 的取值范围．

查看试题解析
20. 如图，抛物线y＝ax²+bx+3（a，b是常数，且a≠0）与x轴交于A、B两点，与y轴交于点C，A、B两点的坐标分别是A（1，0）、B（﹣3，0），抛物线顶点为D

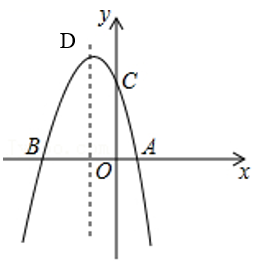(1)、求出抛物线的解析式

(2)、请直接写出顶点D的坐标为；直线BD的解析式为

(3)、若E为线段BD上的一个动点，其横坐标为m，过点E作EF⊥x轴于点F，求当m为何值时，四边形EFOC的面积最大？

(4)、若点P在抛物线的对称轴上，且线段PA绕点P逆时针旋转90°后，点A的对应点A'恰好也落在此抛物线上，请直接写出点P的坐标

查看试题解析
21. 已知抛物线 $y = a x^{2} + c (a \neq 0)$ 经过点 $P (3 ， 0) 、 Q (1 ， 4)$ ，与x轴的另一个交点为C ，点A在线段 $P Q$ 上，过点A作 $A B ⊥ x$ 轴于点B ．

(1)、求抛物线的解析式；

(2)、求 $△ A B C$ 面积的最大值；

(3)、以 $A B$ 为边在其左侧作等腰直角三角形 $A B D$ ，问点D能否落在抛物线上，若能，求出点D的坐标，若不能，请说明理由．

查看试题解析
22. 如图，在平面直角坐标系中，抛物线y＝﹣ $\frac{2}{3} x^{2} + \frac{4}{3} x + 2$ 交x轴于A ， B两点（A在B的左侧），交y轴于点C ．

(1)、求直线BC的解析式；

(2)、求抛物线的顶点及对称轴；

(3)、若点Q是抛物线对称轴上的一动点，线段AQ+CQ是否存在最小值？若存在，求出点Q的坐标；若不存在，说明理由；

(4)、若点P是直线BC上方抛物线上的一个动点，△PBC的面积是否存在最大值？若存在，求出点P的坐标及此时△PBC的面积；若不存在，说明理由．

查看试题解析
23. 某商品的进价为每件40元，售价为每件50元，每个月可卖出210件，如果每件商品的售价上涨1元，则每个月少卖10件（每件售价不能高于65元），设每件商品的售价上涨x元（x为正整数），每个月的销售利润为y元，

(1)、求y与x的函数关系式并直接写出x的取值范围；

(2)、每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？

(3)、若在销售过程中每一件商品有a（a＞2）元的其他费用，商家发现当售价每件不低于57元时，每月的销售利润随x的增大而减小，请求出a的取值范围．

查看试题解析
24. 已知二次函数： $y = a x^{2} - 6 a x - 5 (a \neq 0)$ .

(1)、该二次函数图象的对称轴是，它恒经过两个定点的坐标为；

(2)、在直角坐标系中，点 $A (- 2 ， 0)$ 、点 $B (10 ， 0)$ ，若此二次函数的图象与线段 $A B$ 恰有一个公共点，结合图象，求a的取值范围.

(3)、若该二次函数的最大值为4.
①求二次函数的表达式；

②当 $t \leq x \leq t + 3$ 时，函数的最大值为m，最小值为n，若 $m - n = 5$ ，求t的值.

查看试题解析
25. 如图，抛物线 $C ： y = a x^{2} + b x + c$ 的对称轴为直线 $x = - 1$ ，且抛物线经过 $M (1 ， 0) ， D (0 ， 3)$ 两点，与x轴交于点N.

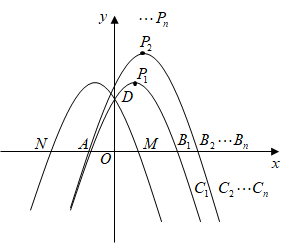(1)、点N的坐标为.

(2)、已知抛物线 $C_{1}$ 与抛物线C关于y轴对称，且抛物线 $C_{1}$ 与x轴交于点 $A ， B_{1}$ （点A在点 $B_{1}$ 的左边）.
①抛物线 $C_{1}$ 的解析式为；
②当抛物线 $C_{1}$ 和抛物线C上y都随x的增大而增大时，请直接写出此时x的取值范围.

(3)、若抛物线 $C_{n}$ 的解析式为 $y = - (x + 1) (x - 2 - n) (n = 1 ， 2 ， 3 ⋯)$ ，抛物线 $C_{n}$ 的顶点为 $P_{n}$ ，与x轴的交点为 $A ， B_{n}$ （点A在点 $B_{n}$ 的左边）.
①求 $A B_{1} + A B_{2} + A B_{3} + ⋯ + A B_{100}$ 的值；
②判断抛物线的顶点 $P_{1} ， P_{2} ， P_{3} ， ⋯ ， P_{n}$ 是否在一条直线上，若在，请直接写出该直线的解析式；若不在，请说明理由.

查看试题解析

销售单价 $x$ （元）	40	60	80
日销售量 $y$ （件）	80	60	40

2022年浙教版数学九上复习阶梯训练：第1章 二次函数 （优生集训）1

一、综合题

2022年浙教版数学九上复习阶梯训练：第1章二次函数（优生集训）1