2022年浙教版数学九上复习阶梯训练:第1章 二次函数 (优生加练)
试卷更新日期:2022-04-22 类型:复习试卷
一、单选题
-
1. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是(
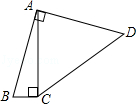 A、y= B、 y= C、 y= D、y=2. 已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设ΔBEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是:( )
A、y= B、 y= C、 y= D、y=2. 已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设ΔBEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是:( )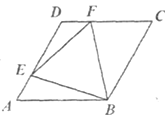 A、
A、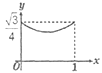 B、
B、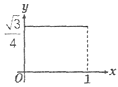 C、
C、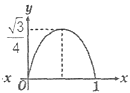 D、
D、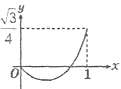 3. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
3. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
 A、4个 B、3个 C、2个 D、1个4. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论不正确的是( )
A、4个 B、3个 C、2个 D、1个4. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=﹣1,下列结论不正确的是( ) A、b2>4ac B、abc>0 C、a﹣c<0 D、am2+bm≥a﹣b(m为为任意实数)5. 已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法不正确的是( )
A、b2>4ac B、abc>0 C、a﹣c<0 D、am2+bm≥a﹣b(m为为任意实数)5. 已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法不正确的是( )x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…
A、a<0 B、方程ax2+bx+c=﹣2的正根在4与5之间 C、2a+b>0 D、若点(5,y1)、(﹣ , y2)都在函数图象上,则y1<y26. 二次函数 的部分图象如图所示,当 时,函数值 的取值范围是( ) A、 B、 C、 D、7. 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
A、 B、 C、 D、7. 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b>2a;③a+b+c=0;④8a+c>0;⑤ax2+bx+c=0的两根分别为﹣3和1.
其中正确的命题有( )
 A、2个 B、3个 C、4个 D、5个8. 将抛物线在x轴上方的部分记为 , 在x轴上及其下方的部分记为 , 将沿x轴向下翻折得到 , 和两部分组成的图象记为M.若直线与M恰有2个交点,则m的取值范围为( )A、或 B、或 C、 D、或9. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A、2个 B、3个 C、4个 D、5个8. 将抛物线在x轴上方的部分记为 , 在x轴上及其下方的部分记为 , 将沿x轴向下翻折得到 , 和两部分组成的图象记为M.若直线与M恰有2个交点,则m的取值范围为( )A、或 B、或 C、 D、或9. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )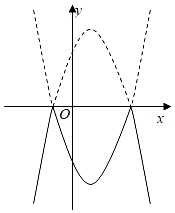 A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣310. 已知抛物线y=﹣x2+bx+c与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),对称轴为l:x=1,直线y=kx+2(k≠0)与抛物线相交于两点M(x1 , y1),N(x2 , y2)(x1<x2),则|x1﹣x2|最小值为( )A、4 B、4 C、2 D、2
A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣310. 已知抛物线y=﹣x2+bx+c与x轴交于点A(m﹣2,0)和B(2m+1,0)(点A在点B的左侧),对称轴为l:x=1,直线y=kx+2(k≠0)与抛物线相交于两点M(x1 , y1),N(x2 , y2)(x1<x2),则|x1﹣x2|最小值为( )A、4 B、4 C、2 D、2二、填空题
-
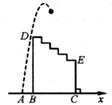
11. 已知抛物线y=-x2+bx+c(b、c为常数).(1)、当c=-4时,抛物线与x轴有且只有一个交点,则b=;(2)、当c=2b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最大值为18,则b的值 .12. 如图是王明正在设计的一动画示意图,×轴上依次有A,B,C三个点,且AB=2,在BC上方有五个台阶(各拐角均为90°),每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10.从点A处向右,上方沿抛物线y=-x2+4x+12发出一个带光的点P.当点P落在台阶上时,落点的坐标是 .
 13. 我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图像(如图所示),并写出下列结论:
13. 我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图像(如图所示),并写出下列结论:①图像与坐标轴的交点为(﹣1,0),(3,0)和(0,3);
②图像具有对称性,对称轴是直线x=1;
③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;
④当x=﹣1或x=3时,函数的最小值是0;
⑤当x=1时,函数的最大值是4;
⑥若点P(a,b)在该图像上,则当b=2时,可以找到4个不同的点P.其中错误的结论是 (填序号).
 14. 如图,已知二次函数 (a≠0(的图象,且关于x的一元二次方程 没有实数根,有下列结论:① ;② ;③ ;④ .其中正确结论的序号有.
14. 如图,已知二次函数 (a≠0(的图象,且关于x的一元二次方程 没有实数根,有下列结论:① ;② ;③ ;④ .其中正确结论的序号有. 15. 如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为 .
15. 如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则面积的最小值为 . 16. 记抛物线C1:y=(x﹣2)2+3的顶点为A,抛物线C2:y=ax2+1(a<0)顶点是点B,且与x轴的正半轴交于点 C.当△ABC是直角三角形时,抛物线C2的解析式为.
16. 记抛物线C1:y=(x﹣2)2+3的顶点为A,抛物线C2:y=ax2+1(a<0)顶点是点B,且与x轴的正半轴交于点 C.当△ABC是直角三角形时,抛物线C2的解析式为.三、综合题
-
17. 如图,在平面直角坐标系中,直线与x轴,y轴相交于A,B两点,点C的坐标是 . 连接AC,BC.
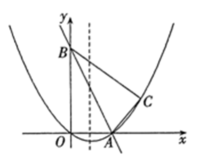 (1)、求过O,A,C三点的抛物线的函数表达式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为ts,当t为何值时,BPQ的面积最大?(3)、当抛物线的对称轴上有一点M,使以A,B,M为顶点的三角形是等腰三角形时,求出点M的坐标.18. 抛物线过点A(-1,0),B(3,0),与y轴交于点C.对称轴与x轴交于点D.
(1)、求过O,A,C三点的抛物线的函数表达式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为ts,当t为何值时,BPQ的面积最大?(3)、当抛物线的对称轴上有一点M,使以A,B,M为顶点的三角形是等腰三角形时,求出点M的坐标.18. 抛物线过点A(-1,0),B(3,0),与y轴交于点C.对称轴与x轴交于点D. (1)、求抛物线的解析式及点D的坐标:(2)、如图,连接CD、CB,在直线BC上方的抛物线上找点P,使得 , 求出P点的坐标:(3)、点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以C,D,M,N为顶点的四边形是菱形?若存在,求出点M的坐标;若不存在,请说明理由.19. 已知:抛物线y=-x2+kx+k+1(k>1)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C.(1)、k=2时,求抛物线的顶点坐标;(2)、若抛物线经过一个定点,求这个定点的坐标;(3)、点P为抛物线上一点,且位于直线BC上方,过点P作PF∥y轴,交BC于点F,求PF长度的最大值(用含k式子表示).20. 已知函数(m为常数),问:(1)、无论m取何值,该函数的图象总经过x轴上某一定点,该定点坐标为;(2)、求证:无论m为何值,该函数的图象顶点都在函数图像上:(3)、若抛物线与x轴有两个交点A、B,且 , 求线段AB的最大值.21. 某童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价2元,每星期可多卖20件.已知该款童装每件成本为40元.设该款童装每件售价为x元,销售量为y件.(1)、每星期的销售量y =(用含x的代数式表示y并化简);(2)、当每件童装售价定为多少元时,该店一星期可获得2210元的利润?(3)、当每件售价定为多少元时,每星期的销售利润最大?最大利润是多少?22. 如图,二次函数y=ax2+bx-3的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)、求抛物线的解析式及点D的坐标:(2)、如图,连接CD、CB,在直线BC上方的抛物线上找点P,使得 , 求出P点的坐标:(3)、点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以C,D,M,N为顶点的四边形是菱形?若存在,求出点M的坐标;若不存在,请说明理由.19. 已知:抛物线y=-x2+kx+k+1(k>1)与x轴交于A、B两点,(点A在点B的左侧),与y轴交于点C.(1)、k=2时,求抛物线的顶点坐标;(2)、若抛物线经过一个定点,求这个定点的坐标;(3)、点P为抛物线上一点,且位于直线BC上方,过点P作PF∥y轴,交BC于点F,求PF长度的最大值(用含k式子表示).20. 已知函数(m为常数),问:(1)、无论m取何值,该函数的图象总经过x轴上某一定点,该定点坐标为;(2)、求证:无论m为何值,该函数的图象顶点都在函数图像上:(3)、若抛物线与x轴有两个交点A、B,且 , 求线段AB的最大值.21. 某童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价2元,每星期可多卖20件.已知该款童装每件成本为40元.设该款童装每件售价为x元,销售量为y件.(1)、每星期的销售量y =(用含x的代数式表示y并化简);(2)、当每件童装售价定为多少元时,该店一星期可获得2210元的利润?(3)、当每件售价定为多少元时,每星期的销售利润最大?最大利润是多少?22. 如图,二次函数y=ax2+bx-3的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.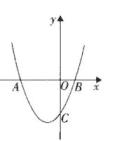 (1)、求该二次函数的表达式;(2)、若点D在x轴的上方,以A、B、D为顶点的三角形与△ABC全等,平移该二次函数图象,使平移后的图象经过点B与点D,请你写出平移过程,并说明理由.23. 我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于直线 (n为常数)对称,则把该函数称之为“ 函数”.(1)、在下列关于x的函数中,是“ 函数”的是(填序号);
(1)、求该二次函数的表达式;(2)、若点D在x轴的上方,以A、B、D为顶点的三角形与△ABC全等,平移该二次函数图象,使平移后的图象经过点B与点D,请你写出平移过程,并说明理由.23. 我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于直线 (n为常数)对称,则把该函数称之为“ 函数”.(1)、在下列关于x的函数中,是“ 函数”的是(填序号);① ,② ,③
(2)、若关于x的函数 (h为常数)是“ 函数”,与 (m为常数, )相交于A( , )、B( , )两点,A在B的左边, ,求m的值;(3)、若关于x的“ 函数” (a,b为常数)经过点( ,1),且 ,当 时,函数的最大值为 ,最小值为 ,且 ,求t的值.24. 如图,在平面直角坐标系中,抛物线 与x轴交于 , 两点(点A在点B的左侧),与y轴交于点C,连接AC、BC,点P为直线BC上方抛物线上一动点,连接OP交BC于点Q. (1)、求抛物线的函数表达式;(2)、当 的值最大时,求点P的坐标和 的最大值;(3)、把抛物线 沿射线AC方向平移 个单位得新抛物线 ,M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,直接写出N点的坐标,并把求其中一个N点坐标的过程写出来.25. 如图1,抛物线 与x轴交于 , 两点,交y轴于点
(1)、求抛物线的函数表达式;(2)、当 的值最大时,求点P的坐标和 的最大值;(3)、把抛物线 沿射线AC方向平移 个单位得新抛物线 ,M是新抛物线上一点,N是新抛物线对称轴上一点,当以M、N、B、C为顶点的四边形是平行四边形时,直接写出N点的坐标,并把求其中一个N点坐标的过程写出来.25. 如图1,抛物线 与x轴交于 , 两点,交y轴于点
 (1)、求抛物线的解析式;(2)、如图2,点P为直线AC上方且抛物线对称轴左侧的抛物线上一点,过点P作х轴的平行线交抛物线于点D,过点P作y轴的平行线交AC于点H,求 的最大值及此时点P的坐标;(3)、把抛物线 向右平移 个单位,再向上平移 个单位得新抛物线,在新抛物线对称轴上找一点M,在新抛物线上找一点N,直接写出所有使得以点A,C,M,N为顶点的四边形是平行四边形的点M的坐标,并把求其中一个点M的坐标的过程写出来.
(1)、求抛物线的解析式;(2)、如图2,点P为直线AC上方且抛物线对称轴左侧的抛物线上一点,过点P作х轴的平行线交抛物线于点D,过点P作y轴的平行线交AC于点H,求 的最大值及此时点P的坐标;(3)、把抛物线 向右平移 个单位,再向上平移 个单位得新抛物线,在新抛物线对称轴上找一点M,在新抛物线上找一点N,直接写出所有使得以点A,C,M,N为顶点的四边形是平行四边形的点M的坐标,并把求其中一个点M的坐标的过程写出来.