2022年浙教版数学九上复习阶梯训练:第1章 二次函数 (提高训练)
试卷更新日期:2022-04-22 类型:复习试卷
一、单选题
-
1. 如图,若抛物线经过原点,则抛物线的解析式为( )
 A、 B、 C、 D、或2. 已知二次函数的图象经过原点,则a的值为( )A、0或2 B、0 C、2 D、无法确定3. 如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标是(3,0),对称轴为直线x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c>0;④当y>0时,﹣1<x<3;⑤b<c.其中正确的个数是( )
A、 B、 C、 D、或2. 已知二次函数的图象经过原点,则a的值为( )A、0或2 B、0 C、2 D、无法确定3. 如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标是(3,0),对称轴为直线x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c>0;④当y>0时,﹣1<x<3;⑤b<c.其中正确的个数是( ) A、2 B、3 C、4 D、54. 将抛物线 向上平移1个单位,平移后所得抛物线的表达式是( )A、 B、 C、 D、 .5. 函数 , 当与时,函数值相等,则当时,函数值等于( )A、-3 B、 C、 D、36. 二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:
A、2 B、3 C、4 D、54. 将抛物线 向上平移1个单位,平移后所得抛物线的表达式是( )A、 B、 C、 D、 .5. 函数 , 当与时,函数值相等,则当时,函数值等于( )A、-3 B、 C、 D、36. 二次函数y=ax2+bx+c的自变量x和函数y的部分对应值如表:x
…
0
1
2
3
4
…
y
…
4
5
4
﹣4
﹣20
﹣45
…
则该二次函数y在所给自变量x(﹣2≤x≤2)的取值范围内的最小值是( )
A、﹣45 B、﹣20 C、﹣4 D、07. 已知二次函数 (其中m>0),下列说法正确的是( )A、当x>2时,都有y随着x的增大而增大 B、当x<3时,都有y随着x的增大而减小 C、若x<n时,都有y随着x的增大而减小,则 D、若x<n时,都有y随着x的增大而减小,则8. 如图,函数的图象过点和 , 请思考下列判断: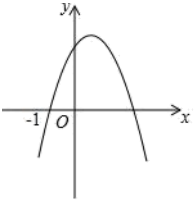
①;②;③;④;⑤.
正确的是( )
A、①③⑤ B、①③④ C、①②③④⑤ D、①②③⑤9. 在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大.收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”P的可能性最大的线路是( ) A、 B、 C、 D、10. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )A、55 B、56 C、57 D、58
A、 B、 C、 D、10. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )A、55 B、56 C、57 D、58二、填空题
-
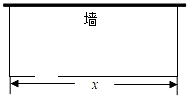
11. 二次函数y=ax+bx+c(a≠0)的图象过点A(0,1)和C(-1,0)(1)、若函数图象的对称轴是x=-1,则函数解析式为(2)、当a=-2时,作直线x=h(h>0)交直线AC于P,交抛物线于点Q,交x轴于点D,当PQ=QD时,h=12. 如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式:.(不用写x的取值范围)
 13. 若把函数y=x的图象用E(x,x)记,函数y=2x+1的图象用E(x,2x+1)记,……则E(x, )图象上的最低点是.14. 二次函数y=ax2+bx+c的图象如图所示,虚线为其对称轴,有下列结论:①abc<0;②b2-4ac<0;③4a+2b+c<0;④若点(-2,y1),(15,y2)均在抛物线上,则y1<y2.其中正确的有个.
13. 若把函数y=x的图象用E(x,x)记,函数y=2x+1的图象用E(x,2x+1)记,……则E(x, )图象上的最低点是.14. 二次函数y=ax2+bx+c的图象如图所示,虚线为其对称轴,有下列结论:①abc<0;②b2-4ac<0;③4a+2b+c<0;④若点(-2,y1),(15,y2)均在抛物线上,则y1<y2.其中正确的有个. 15. 如图所示的抛物线是二次函数的图象,那么的值是.
15. 如图所示的抛物线是二次函数的图象,那么的值是.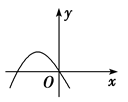 16. 若二次函数 的图象经过点 ,则 的值为.
16. 若二次函数 的图象经过点 ,则 的值为.三、计算题
-
17. 求不等式﹣x2﹣6x+16>0的解集.18.(1)、解方程:2x2+1=3x;(2)、将二次函数 配方成y=a(x﹣h)2+k的形式.
四、综合题
-
19. 如图,在平面直角坐标系中,一次函数的图象与x轴、y轴分别交于点A,B,且 , , 同时交反比例函数在第一象限的图象于点 , 反比例函数图象上的点P的纵坐标 , 轴交直线AB于点Q,D是x轴上任意一点,连接PD,QD.
 (1)、求一次函数和反比例函数的表达式;(2)、求△PDQ面积的最大值.20. 2022年北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民的喜爱.某特许零售店“冰墩墩”的销售日益火爆.每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为y个,销售单价为x元.(1)、直接写出y与x之间的函数关系式和自变量x的取值范围;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?(3)、该店主热心公益事业,决定从每天的利润中捐出200元给希望工程,为了保证捐款后每天剩余利润不低于2200元,求销售单价x的范围.21. 某商贸公司购进某种商品的成本为20元/千克,经过市场调研发现,这种商品在未来40天的销售单价y(元/千克)与时间×(天)之间的函数关系式为:y= ,且×为整数,且日销量m(千克)与时间×(天)之间的变化规律符合一次函数关系,如下表:
(1)、求一次函数和反比例函数的表达式;(2)、求△PDQ面积的最大值.20. 2022年北京冬奥会举办期间,冬奥会吉祥物“冰墩墩”深受广大人民的喜爱.某特许零售店“冰墩墩”的销售日益火爆.每个纪念品进价40元,规定销售单价不低于44元,且不高于52元.销售期间发现,当销售单价定为44元时,每天可售出300个,销售单价每上涨1元,每天销量减少10个.现商家决定提价销售,设每天销售量为y个,销售单价为x元.(1)、直接写出y与x之间的函数关系式和自变量x的取值范围;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?(3)、该店主热心公益事业,决定从每天的利润中捐出200元给希望工程,为了保证捐款后每天剩余利润不低于2200元,求销售单价x的范围.21. 某商贸公司购进某种商品的成本为20元/千克,经过市场调研发现,这种商品在未来40天的销售单价y(元/千克)与时间×(天)之间的函数关系式为:y= ,且×为整数,且日销量m(千克)与时间×(天)之间的变化规律符合一次函数关系,如下表:时间x(天)
1
3
6
10
……
日销量m(千克)
142
138
132
124
……
(1)、求m与×的函数关系式;(2)、当1≤×≤20时,最大日销售利润是多少?(3)、求:在未来40天中,有多少天销售利润不低于1550元?