北师大版备考2022中考数学二轮复习专题22 与圆有关的位置关系
试卷更新日期:2022-04-22 类型:二轮复习
一、单选题
-
1. 如图,AB、AC是⊙O的切线,B、C为切点,点D是优弧BC上一点,∠BDC=70°, 则∠A的度数是( )
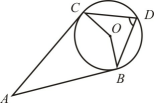 A、20° B、40° C、55° D、70°2. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
A、20° B、40° C、55° D、70°2. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )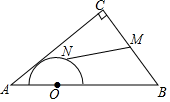 A、5 B、6 C、7 D、83. 如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( )
A、5 B、6 C、7 D、83. 如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( ) A、 B、 C、2 D、4.
A、 B、 C、2 D、4.如图所示,⊙M与x轴相切于原点,平行于y轴的直线交圆于P,Q两点,P点在Q点的下方,若P点坐标是(2,1),则圆心M的坐标是( )
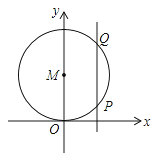 A、(0,3) B、(0,2) C、(0,) D、(0,)5. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
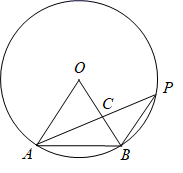
A、(0,3) B、(0,2) C、(0,) D、(0,)5. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )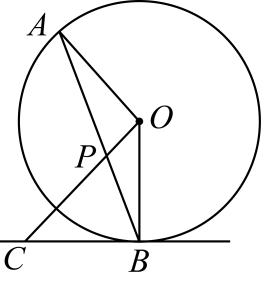 A、 B、 C、 D、6. 如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为( )
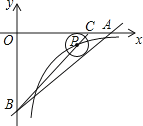
A、 B、 C、 D、6. 如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为( )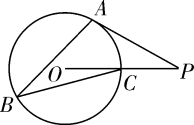 A、2 B、 C、 D、7. 如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
A、2 B、 C、 D、7. 如图所示,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(﹣3,0),B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )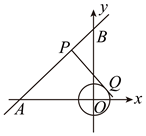 A、 B、2.4 C、 D、38. 如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A、 B、2.4 C、 D、38. 如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )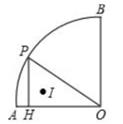 A、 B、 C、 D、π9. 如图,一把直尺, 60°的直角三角板和光盘如图摆放, A为 60°角与直尺交点, AB=3 ,则光盘的直径是( )
A、 B、 C、 D、π9. 如图,一把直尺, 60°的直角三角板和光盘如图摆放, A为 60°角与直尺交点, AB=3 ,则光盘的直径是( )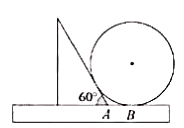 A、3 B、 C、 D、10. 如图,抛物线y= x2﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )
A、3 B、 C、 D、10. 如图,抛物线y= x2﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )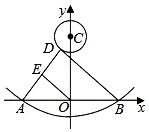 A、 B、 C、3 D、2
A、 B、 C、3 D、2二、填空题
-
11. 是的内接正六边形一边,点P是优弧上的一点(点P不与点A,B重合)且 , 与交于点C,则的度数为 .
 12. 在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,则以2.4cm为半径的⊙C与直线AB的关系是.13. 如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是。
12. 在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,则以2.4cm为半径的⊙C与直线AB的关系是.13. 如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是。 14.
14.如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=(k≠0)的图象经过圆心P,则k= .
 15. 如图,半径为 2 的⊙O 与正六边形 ABCDEF 相切于点 C,F,则图中阴影部分的面积为.
15. 如图,半径为 2 的⊙O 与正六边形 ABCDEF 相切于点 C,F,则图中阴影部分的面积为.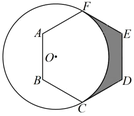 16. 已知△ABC的边BC=4cm,⊙O是其外接圆,且半径也为4cm,则∠A的度数是 .17. 已知⊙O的半径为R,点O到直线m的距离为d,R、d是方程x2-4x+a=0的两根,当直线m与⊙O相切时,a=.18. 如图,在 中, 的半径为1,点P是 边上的动点,过点P作 的一条切线 (其中点Q为切点),则线段 长度的最小值为 .
16. 已知△ABC的边BC=4cm,⊙O是其外接圆,且半径也为4cm,则∠A的度数是 .17. 已知⊙O的半径为R,点O到直线m的距离为d,R、d是方程x2-4x+a=0的两根,当直线m与⊙O相切时,a=.18. 如图,在 中, 的半径为1,点P是 边上的动点,过点P作 的一条切线 (其中点Q为切点),则线段 长度的最小值为 .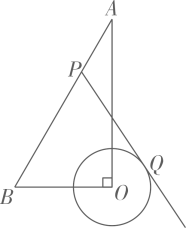
三、作图题
-
19.
如图,有一块三角形材料(△ABC),请你画出一个圆,使其与△ABC的各边都相切.
.
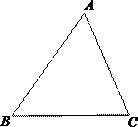 20. 如图,已知△ABC,用尺规作出△ABC外心.(保留作图痕迹,不写作法)
20. 如图,已知△ABC,用尺规作出△ABC外心.(保留作图痕迹,不写作法)
四、解答题
-
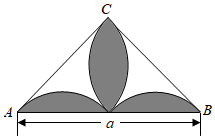
21. 如图,是以为斜边的等腰直角三角形,其内部的4段弧均等于以BC为直径的圆周,求图中阴影部分的面积.
 22.
22.如图,AB、CD为 O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使 PED= C.
 (1)、求证:PE是 O的切线;
(1)、求证:PE是 O的切线;
(2)、求证:ED平分 BEP;
(3)、若 O的半径为5,CF=2EF,求PD的长.
五、综合题
-
23. 已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
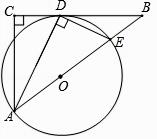 (1)、求证:BC是⊙O的切线;(2)、若AC=3,BC=4,求BE的长.24. 如图1,在平面直角坐标系中,已知点 , 以O为圆心,OA为半径作 , 交y轴于点C,直线l:经过点C.
(1)、求证:BC是⊙O的切线;(2)、若AC=3,BC=4,求BE的长.24. 如图1,在平面直角坐标系中,已知点 , 以O为圆心,OA为半径作 , 交y轴于点C,直线l:经过点C. (1)、设直线l与的另一个交点为如图 , 求弦CD的长;(2)、将直线l向上平移2个单位,得直线m,如图2,求证:直线m与相切;(3)、在的前提下,设直线m与切于点P,Q为上一动点,过点P作 , 交直线QA于点如图 , 则的最大面积为 .25. 如图,ΔDBE内接于⊙O,BD为直径,DE=EB,点C在⊙O(不与D,B,E重合)上,∠A=45°,点A在直线CD上,连接AB.
(1)、设直线l与的另一个交点为如图 , 求弦CD的长;(2)、将直线l向上平移2个单位,得直线m,如图2,求证:直线m与相切;(3)、在的前提下,设直线m与切于点P,Q为上一动点,过点P作 , 交直线QA于点如图 , 则的最大面积为 .25. 如图,ΔDBE内接于⊙O,BD为直径,DE=EB,点C在⊙O(不与D,B,E重合)上,∠A=45°,点A在直线CD上,连接AB.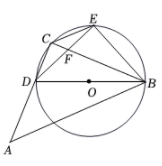 (1)、如图1,若点C在DE上,求证:ΔABD~ΔCBE;(2)、在(1)的条件下,DC=6,DB=10,求线段CE的长;(3)、若直线BC与直线DE相交于点F,当 时,求 的值。
(1)、如图1,若点C在DE上,求证:ΔABD~ΔCBE;(2)、在(1)的条件下,DC=6,DB=10,求线段CE的长;(3)、若直线BC与直线DE相交于点F,当 时,求 的值。