北师大版备考2022中考数学二轮复习专题20 特殊平行四边形
试卷更新日期:2022-04-20 类型:二轮复习
一、单选题
-
1.
如图,在平面直角坐标系 中,已知点 , .若平移点 到点 ,使以点 , , , 为顶点的四边形是菱形,则正确的平移方法是( )
 A、向左平移1个单位,再向下平移1个单位 B、向左平移 个单位,再向上平移1个单位 C、向右平移 个单位,再向上平移1个单位 D、向右平移1个单位,再向上平移1个单位2. 一副三角板按如图所示的位置摆放,若 ,则 的度数是( )
A、向左平移1个单位,再向下平移1个单位 B、向左平移 个单位,再向上平移1个单位 C、向右平移 个单位,再向上平移1个单位 D、向右平移1个单位,再向上平移1个单位2. 一副三角板按如图所示的位置摆放,若 ,则 的度数是( ) A、 B、 C、 D、3. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
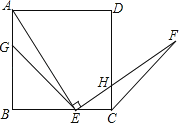
A、 B、 C、 D、3. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )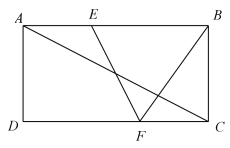 A、 B、 C、4 D、64. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
A、 B、 C、4 D、64. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=GE; ②△AGE≌△ECF; ③∠FCD=45°; ④△GBE∽△ECH,其中,正确的结论有( )
 A、1个 B、2个 C、3个 D、4个5. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )
A、1个 B、2个 C、3个 D、4个5. 如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )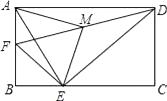 A、5 B、 C、 D、6. 如图,菱形ABCD的顶点分别在反比例函数y = 和y= 的图象上,若∠BCD=60°,则 的值是( )
A、5 B、 C、 D、6. 如图,菱形ABCD的顶点分别在反比例函数y = 和y= 的图象上,若∠BCD=60°,则 的值是( ) A、- B、- C、- D、-7. 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
A、- B、- C、- D、-7. 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )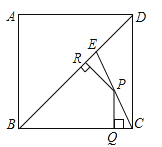 A、2 B、2 C、2 D、8.
A、2 B、2 C、2 D、8.如图,正方形ABCD的对角线交于点O , 以AD为边向外作Rt△ADE , ∠AED=90°,连接OE , DE=6,OE= ,则另一直角边AE的长为( ).
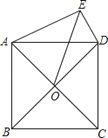 A、 B、2 C、8 D、109. 如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )
A、 B、2 C、8 D、109. 如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )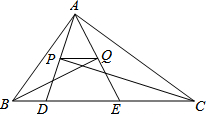 A、 B、 C、3 D、410. 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , ………按这样的规律进行下去,第2012个正方形的面积为( )
A、 B、 C、3 D、410. 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1 , ………按这样的规律进行下去,第2012个正方形的面积为( )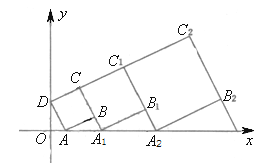 A、5()2010 B、5()2010 C、5()2012 D、5()4022
A、5()2010 B、5()2010 C、5()2012 D、5()4022二、填空题
-
11. 在矩形ABCD中, , , E是BC的中点,连接AE,过点D作于点F,连接CF、AC.(1)、线段DF的长为;(2)、若AC交DF于点M,则 .12. 如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为 .
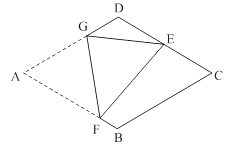 13. 在 中,D为BC中点,将 沿AD折叠,得到 ,连接EC,若已知 ,且 ,则点E到AD的距离为.
13. 在 中,D为BC中点,将 沿AD折叠,得到 ,连接EC,若已知 ,且 ,则点E到AD的距离为.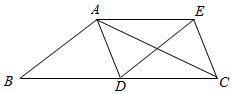 14. 如图,正方形ABCD的边长为10,E、F分别是BC、CD边上的点, , 分别连接AE、BF,两线段交于一点M,点G、H分别是AE、BF边上的中点.
14. 如图,正方形ABCD的边长为10,E、F分别是BC、CD边上的点, , 分别连接AE、BF,两线段交于一点M,点G、H分别是AE、BF边上的中点.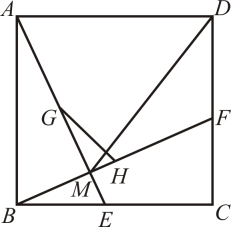 (1)、当BE=4时,线段GH的长为 .(2)、连结DM,当时,= .15. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.
(1)、当BE=4时,线段GH的长为 .(2)、连结DM,当时,= .15. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.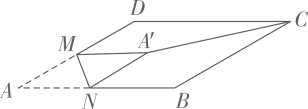 16. 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
16. 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若= , 则3S△BDG=13S△DGF .
其中正确的结论是 (写所有正确结论的序号).
 17. 如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=EH,那么EH的长为 .
17. 如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=EH,那么EH的长为 .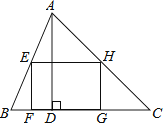 18. 如图,矩形ABCD中,AB=9,AD=12,点M在对角线BD上,点N为射线BC上一动点,连接MN,DN,且∠DNM=∠DBC,当DMN是等腰三角形时,线段BN的长为 .
18. 如图,矩形ABCD中,AB=9,AD=12,点M在对角线BD上,点N为射线BC上一动点,连接MN,DN,且∠DNM=∠DBC,当DMN是等腰三角形时,线段BN的长为 .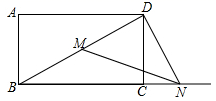
三、作图题
-
19. 在图①②中,点E在矩形ABCD的边BC上,且BE=AB,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法]
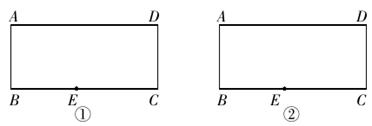 (1)、在图①中,画∠BAD的平分线;(2)、在图②中,画∠BCD的平分线.
(1)、在图①中,画∠BAD的平分线;(2)、在图②中,画∠BCD的平分线.四、解答题
-
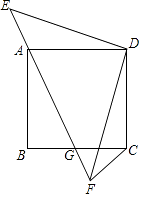
20. 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
 21. 如图,在线段AD上有两点E,F,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且AB∥CD.求证:四边形BECF是平行四边形。
21. 如图,在线段AD上有两点E,F,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且AB∥CD.求证:四边形BECF是平行四边形。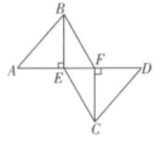
五、综合题
-
22.
已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.
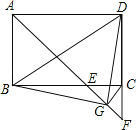
 (1)、求证:△BCG≌△DCE;(2)、将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由。23. 如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG//CD交BE于点G,连结CG.
(1)、求证:△BCG≌△DCE;(2)、将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由。23. 如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG//CD交BE于点G,连结CG.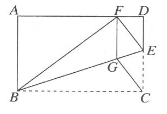 (1)、求证:四边形CEFG是菱形;(2)、若AB=6,AD=10,求四边形CEFG的面积.24. 如图,在平面直角坐标系中,点A,B的坐标分别是(﹣4,0),(0,8),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造▱PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
(1)、求证:四边形CEFG是菱形;(2)、若AB=6,AD=10,求四边形CEFG的面积.24. 如图,在平面直角坐标系中,点A,B的坐标分别是(﹣4,0),(0,8),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造▱PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.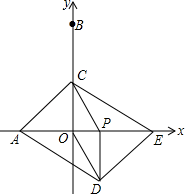 (1)、当点C运动到线段OB的中点时,求t的值及点E的坐标;(2)、当点C在线段OB上时,求证:四边形ADEC为平行四边形;(3)、在线段PE上取点F,使PF=3,过点F作MN⊥PE,截取FM= ,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.
(1)、当点C运动到线段OB的中点时,求t的值及点E的坐标;(2)、当点C在线段OB上时,求证:四边形ADEC为平行四边形;(3)、在线段PE上取点F,使PF=3,过点F作MN⊥PE,截取FM= ,FN=1,且点M,N分别在第一、四象限,在运动过程中,当点M,N中,有一点落在四边形ADEC的边上时,直接写出所有满足条件的t的值.
-