北师大版备考2022中考数学二轮复习专题19 多边形与平行四边形

试卷更新日期：2022-04-20 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，五边形ABCDE的每一个内角都相等，则外角∠CBF等于（）

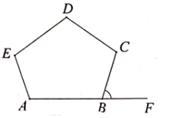A、60° B、72° C、80° D、108°

查看试题解析
2. 如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，过点C作CI⊥HJ于点I，交AB于K，在图形的外部作矩形MNPQ，使点D，E，G和H，J都落在矩形的边上.已知矩形BJIK的面积为1，正方形ACDE的面积为4，则 $\frac{M N}{M Q}$ 为（）

A、 $\frac{1}{2}$ B、 $\frac{7}{11}$ C、 $\frac{8}{11}$ D、 $\frac{9}{11}$

查看试题解析
3. 一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是（　　）

A、27 B、35 C、44 D、54

查看试题解析
4.
如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（　　）
①∠DCF= $\frac{1}{2}$ ∠BCD；②EF=CF；③S_△_BEC=2S_△_CEF；④∠DFE=3∠AEF．

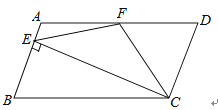A、①② B、②③④ C、①②④ D、①②③④

查看试题解析
5. 如图，在五边形ABCDE中，∠A+∠B+∠E=∠EDC+∠BCD+140°，DF，CF分别平分∠EDC和∠BCD，则∠F的度数为（　　）

A、100° B、90° C、80° D、70°

查看试题解析
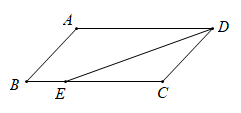
6.
如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（　　）

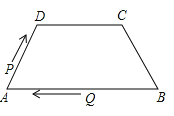A、4s B、3s C、2s D、1s

查看试题解析
7.
如图，在平面直角坐标系中，以O（0，0）、A（1，-1）、B（2，0）为顶点，构造平行四边形，下列各点中不能作为平行四边形第四个顶点坐标的是（　　　）

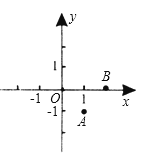A、（3，-1） B、（-1，-1） C、（1，1） D、（-2，-1）

查看试题解析
8. 如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°， $A B = \frac{1}{2} B C = 1$ ，则下列结论：①∠CAD=30° ② $B D = \sqrt{7}$ ③S_{平行四边形ABCD}=AB•AC ④ $O E = \frac{1}{4} A D$ ，正确的个数是（）

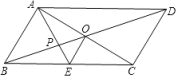A、1 B、2 C、3 D、4

查看试题解析
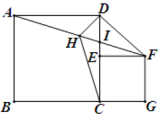9. 如图，正方形ABCD中，点E是边CD上的动点（不与点C、D重合），以CE为边向右作正方形CEFG，连接AF，点H是AF的中点，连接DH、CH．下列结论：①△ADH≌△CDH；②AF平分∠DFE；③若BC＝4，CG＝3，则AF＝5；④若 $\frac{C G}{B C} = \frac{1}{2}$ ，则 $\frac{S_{Δ E F I}}{S_{Δ D F I}} = \frac{1}{4}$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，矩形ABCD的面积为1cm² ，对角线交于点O；以AB、AO为邻边作平行四边形AOC₁B，对角线交于点O₁；以AB、AO₁为邻边作平行四边形AO₁C₂B…；依此类推，则平行四边形AO₂₀₁₄C₂₀₁₅B的面积为（）

A、 $\frac{1}{2^{2013}}$ B、 $\frac{1}{2^{2014}}$ C、 $\frac{1}{2^{2015}}$ D、 $\frac{1}{2^{2016}}$

查看试题解析

二、填空题

11. 如图，在平行四边形 $A B C D$ 中， $D E$ 平分 $∠ A D C$ ， $A D = 5$ ， $B E = 2$ ，则 $A B C D$ 的周长是.

查看试题解析
12.
如图，已知四边形ABCD中，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，则∠1+∠2=°．

查看试题解析
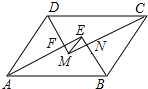
13.
如图，▱ABCD中，AB＞AD，AE，BE，CM，DM分别为∠DAB，∠ABC，∠BCD，∠CDA的平分线，AE与DM相交于点F，BE与CM相交于点N，连接EM．若▱ABCD的周长为42cm，FM=3cm，EF=4cm，则EM= cm，AB= cm．

查看试题解析
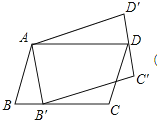
14.
如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=

查看试题解析
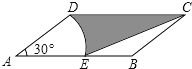
15.
如图，在▱ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是（结果保留π）.

查看试题解析
16. 如图，已知▱OABC的顶点A、C分别在直线x=1和x=4上，O是坐标原点，则对角线OB长的最小值为．

查看试题解析
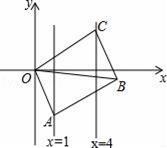17. 如图，菱形ABC的对角线相交于点O，过点D作DE∥AC，且DE= AC，连接CE、OE、AE，AE交OD于点F，若AB=2，∠ABC=60°，则AE的长．

查看试题解析
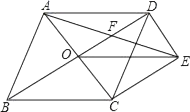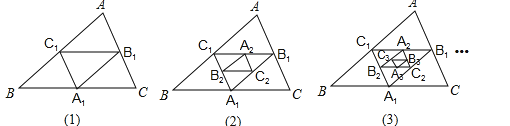
18.
如图，在图（1）中，A₁、B₁、C₁分别是△ABC的边BC、CA、AB的中点，在图（2）中，A₂、B₂、C₂分别是△A₁B₁C₁的边B₁C₁、C₁A₁、A₁B₁的中点，…，按此规律，则第n个图形中平行四边形的个数共有个

查看试题解析

三、作图题

19. 已知∠MON=α，P为射线OM上的点，OP=1．

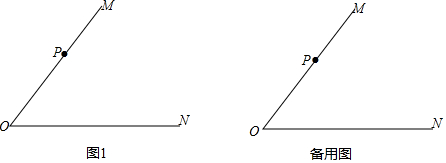(1)、如图1，α=60°，A，B均为射线ON上的点，OA=1，OB＞OA，△PBC为等边三角形，且O，C两点位于直线PB的异侧，连接AC．
①依题意将图1补全；

②判断直线AC与OM的位置关系并加以证明；

(2)、若α=45°，Q为射线ON上一动点（Q与O不重合），以PQ为斜边作等腰直角△PQR，使O，R两点位于直线PQ的异侧，连接OR．根据（1）的解答经验，直接写出△POR的面积．

查看试题解析

四、综合题

20.
如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．

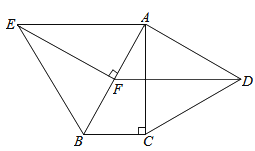(1)、试说明AC=EF；

(2)、求证：四边形ADFE是平行四边形.

查看试题解析
21. 如图，平行四边形ABCO位于直角坐标系中，O为坐标原点，点 $A (- 8 ， O)$ ，点 $C (3 ， 4) B C$ 交y轴于点 $D .$ 动点E从点D出发，沿DB方向以每秒1个单位长度的速度终点B运动，同时动点F从点A出发，沿射线OA的方向以每秒2个单位长度的速度运动，当点E运动到点B时，点F随之停止运动，运动时间为 $f 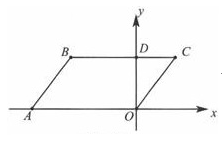($ 秒 $)$ .

(1)、用t的代数式表示： $B E =$ ， $O F =$

(2)、若以A，B，E，F为顶点的四边形是平行四边形时，求t的值.

(3)、当 $△ B E F$ 恰好是等腰三角形时，求t的值.

查看试题解析
22. 如图，矩形OABC在平面直角坐标系中，若x²-2 $\sqrt{3}$ x+2=0的两根是x₁、x₂ ，且OC=x₁+x₂ ， OA=x₁x₂

(1)、求B点的坐标.

(2)、把△ABC沿AC对折，点B落在点B′处，线段AB′与x轴交于点D，求直线BD的解析式．

(3)、在平面上是否存在点P，使D、C、B、P四点形成的四边形为平形四边形？若存在，请直接写出P 点坐标；若不存在，请说明理由.

查看试题解析
23.
如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．

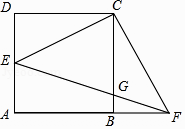(1)、求证：△CDE≌△CBF；

(2)、当DE= $\frac{1}{2}$ 时，求CG的长；

(3)、连结AG，在点E运动过程中，四边形CEAG能否为平行四边形？若能，求出此时DE的长；若不能，说明理由．

查看试题解析