北师大版备考2022中考数学二轮复习专题18 解直角三角形
试卷更新日期:2022-04-20 类型:二轮复习
一、单选题
-
1. 某楼梯的侧面如图所示,已测得BC的长约为3.5米,∠BCA约为29°,则该楼梯的高度AB可表示为( )
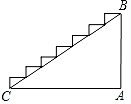 A、3.5sin29° B、3.5cos29° C、3.5tan29° D、2. 如图,在Rt△ABC中,∠B=90°,AB=8,BC=6,延长BC至E,使得CE=BC,将△ABC沿AC翻折,使点B落点D处,连接DE,则DE的长为( )
A、3.5sin29° B、3.5cos29° C、3.5tan29° D、2. 如图,在Rt△ABC中,∠B=90°,AB=8,BC=6,延长BC至E,使得CE=BC,将△ABC沿AC翻折,使点B落点D处,连接DE,则DE的长为( ) A、 B、 C、 D、3. 某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )
A、 B、 C、 D、3. 某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )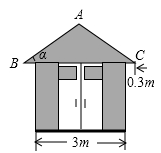 A、 米 B、 米 C、 米 D、 米4. 如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A、 米 B、 米 C、 米 D、 米4. 如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( ) A、2 B、3 C、4 D、4-5. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则 可以是( )
A、2 B、3 C、4 D、4-5. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则 可以是( )20
a
A、 B、-1 C、0 D、6. 如图钓鱼竿AC长6m,露在水面上的鱼线BC长3 m,钓者想看看鱼上钩的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )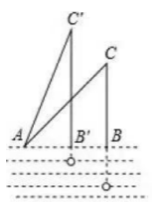 A、3m B、m C、m D、4m7. 如图,正方形ABCD中,内部有4个全等的正方形,小正方形的顶点E,F,G,H分别在边AB,BC,CD,AD上,则tan∠AEH=( )
A、3m B、m C、m D、4m7. 如图,正方形ABCD中,内部有4个全等的正方形,小正方形的顶点E,F,G,H分别在边AB,BC,CD,AD上,则tan∠AEH=( )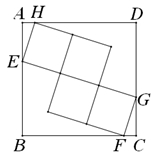 A、 B、 C、 D、8. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( )
A、 B、 C、 D、8. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形 ,若 ,则菱形 的面积与正方形ABCD的面积之比是( ) A、1 B、 C、 D、9. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α , ∠ADC=β , 则竹竿AB与AD的长度之比为( )
A、1 B、 C、 D、9. 如图,两根竹竿AB和AD斜靠在墙CE上,量得∠ABC=α , ∠ADC=β , 则竹竿AB与AD的长度之比为( )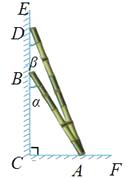 A、 B、 C、 D、10. 如图,在四边形ABCD中, , , ,AC与BD交于点E, ,则 的值是( )
A、 B、 C、 D、10. 如图,在四边形ABCD中, , , ,AC与BD交于点E, ,则 的值是( )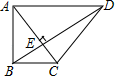 A、 B、 C、 D、11. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )
A、 B、 C、 D、11. 如图,在边长为2的正方形ABCD中,若将AB绕点A逆时针旋转 ,使点B落在点 的位置,连接B ,过点D作DE⊥ ,交 的延长线于点E,则 的长为( )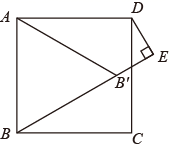 A、 B、 C、 D、12. 如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为( )
A、 B、 C、 D、12. 如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为( )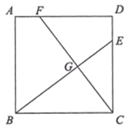 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知α、β均为锐角,且满足|sinα﹣|+=0,则α+β= .
14. 如图,在矩形ABCD中,点E是AD的中点,连接AC,EC,CD=DE,则tan∠ACE的值为.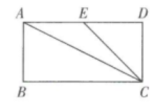 15. 如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为。
15. 如图,在菱形ABCD中,AB=2,∠B是锐角,AE⊥BC于点E,M是AB的中点,连结MD,ME.若∠EMD=90°,则cosB的值为。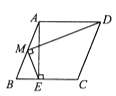 16. 如图,在△ABC中,∠B=45°,AB=6 ,D、E分别是AB、AC的中点,连接DE,在直线DE和直线BC上分别取点F、G,连接BF、DG.若BF=2DG,且直线BF与直线DG互相垂直,则BG的长为 .
16. 如图,在△ABC中,∠B=45°,AB=6 ,D、E分别是AB、AC的中点,连接DE,在直线DE和直线BC上分别取点F、G,连接BF、DG.若BF=2DG,且直线BF与直线DG互相垂直,则BG的长为 . 17. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm.
17. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm. 18. 如图,在矩形ABCD中,AB= ,AD=3,点P是AD边上的一个动点,连接BP,作点A关于直线BP的对称点A1 , 连接A1C,设A1C的中点为Q,当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为.
18. 如图,在矩形ABCD中,AB= ,AD=3,点P是AD边上的一个动点,连接BP,作点A关于直线BP的对称点A1 , 连接A1C,设A1C的中点为Q,当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为.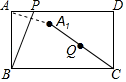 19. 如图,△ABC内接于半径为 的半圆O中,AB为直径,点M是 的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,∠ADB=135°且D为BM的中点,则DM的长为;BC的长为.
19. 如图,△ABC内接于半径为 的半圆O中,AB为直径,点M是 的中点,连结BM交AC于点E,AD平分∠CAB交BM于点D,∠ADB=135°且D为BM的中点,则DM的长为;BC的长为. 20. 如图,在平面直角坐标系中,点A在y轴的正半轴上,OA=1,将OA绕点O顺时针旋转45°到OA1 , 扫过的面积记为S1 , A1A2⊥OA1交x轴于点A2;将OA2绕点O顺时针旋转45°到OA3 , 扫过的面积记为S2 , A3A4⊥OA3交y轴于点A4;将OA4绕点O顺时针旋转45°到OA5 , 扫过的面积记为S3;…;按此规律,则S2021为 .
20. 如图,在平面直角坐标系中,点A在y轴的正半轴上,OA=1,将OA绕点O顺时针旋转45°到OA1 , 扫过的面积记为S1 , A1A2⊥OA1交x轴于点A2;将OA2绕点O顺时针旋转45°到OA3 , 扫过的面积记为S2 , A3A4⊥OA3交y轴于点A4;将OA4绕点O顺时针旋转45°到OA5 , 扫过的面积记为S3;…;按此规律,则S2021为 .
三、计算题
-
21. 计算:|﹣4|﹣2cos60°+( ﹣ )0﹣(﹣3)2 .22. 计算:|-3|+(π-3)0- +tan45°
四、作图题
-
23. 如图在的正方形的网格中,每个小正方形的边长为1,线段、的端点均在小正方形的顶点上.

⑴在图中的为边画 , 使点在小正方形的顶点上,且.
⑵在(1)的条件下,在图中的以为边画面积为3的使点在小正方形的顶点上, , 连结直接写出线段的长.
五、综合题
-
24. 如图1,已知在平面直角坐标系xOy中,四边形OABC是矩形点A,C分别在x轴和y轴的正半轴上,连结AC,OA=3,tan∠OAC= ,D是BC的中点.
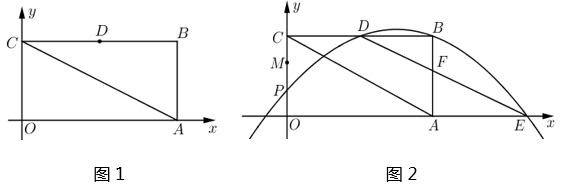 (1)、求OC的长和点D的坐标;(2)、如图2,M是线段OC上的点,OM= OC,点P是线段OM上的一个动点,经过P,D,B三点的抛物线交x轴的正半轴于点E,连结DE交AB于点F
(1)、求OC的长和点D的坐标;(2)、如图2,M是线段OC上的点,OM= OC,点P是线段OM上的一个动点,经过P,D,B三点的抛物线交x轴的正半轴于点E,连结DE交AB于点F①将△DBF沿DE所在的直线翻折,若点B恰好落在AC上,求此时BF的长和点E的坐标;
②以线段DF为边,在DF所在直线的右上方作等边△DFG,当动点P从点O运动到点M时,点G也随之运动,请直接写出点G运动路径的长.
25. 如图1,在平面直角坐标系中,点 在x轴负半轴上,点B在y轴正半轴上,设 ,且 . (1)、直接写出 的度数.(2)、如图2,点D为AB的中点,点P为y轴负半轴上一点,以AP为边作等边三角形APQ,连接DQ并延长交x轴于点M,若 ,求点M的坐标.(3)、如图3,点C与点A关于y轴对称,点E为OC的中点,连接BE,过点B作 ,且 ,连接AF交BC于点P,求 的值.
(1)、直接写出 的度数.(2)、如图2,点D为AB的中点,点P为y轴负半轴上一点,以AP为边作等边三角形APQ,连接DQ并延长交x轴于点M,若 ,求点M的坐标.(3)、如图3,点C与点A关于y轴对称,点E为OC的中点,连接BE,过点B作 ,且 ,连接AF交BC于点P,求 的值.
-