吉林省长春市2022届高三理数线上质量监测试卷（三）

试卷更新日期：2022-04-20 类型：高考模拟

进入出卷网下载

一、单选题

1. 集合 $A = {x | - 1 \leq x < 2} ， B = {x | x > 1}$ ，则 $A ∩ (∁_{R} B) =$ （）

A、 ${x | - 1 \leq x < 1}$ B、 ${x | - 1 \leq x \leq 1}$ C、 ${x | 1 \leq x < 2}$ D、 ${x | x < 2}$

查看试题解析
2. 在复平面内，复数 $\frac{5 i}{2 + i}$ 对应的点坐标为（）

A、 $(1 ， 2)$ B、 $(1 ， - 2)$ C、 $(- 1 ， 2)$ D、 $(- 1 ， - 2)$

查看试题解析
3. 已知 $a \in (0 ， + \infty)$ ，则“ $a > 1$ ”是“ $a + \frac{1}{a} > 2$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
4. 抛物线 $C ： x^{2} = 4 a y$ 过点 $(- 4 ， 4)$ ，则 $C$ 的准线方程为（）

A、 $y = 1$ B、 $y = - 1$ C、 $x = 1$ D、 $x = - 1$

查看试题解析
5. 已知平面向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = 2$ ， $| \vec{b} | = 1$ ，且 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{2 π}{3}$ ，则 $| \vec{a} + \vec{b} | =$ （）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{7}$ D、3

查看试题解析
6. 某区创建全国文明城市，指挥部办公室对所辖街道当月文明城市创建工作进行考评．工作人员在本区选取了甲、乙两个街道，并在这两个街道各随机抽取10个地点进行现场测评，下表是两个街道的测评分数（满分100分），则下列说法正确的是（）
甲
75
79
82
84
86
87
90
91
93
98
乙
73
81
81
83
87
88
95
96
97
99

A、甲、乙两个街道的测评分数的极差相等 B、甲、乙两个街道的测评分数的平均数相等 C、街道乙的测评分数的众数为87 D、甲、乙两个街道测评分数的中位数中，乙的中位数较大

查看试题解析
7. 设 $m \in (0 ， 1)$ ，若 $a = l g m$ ， $b = l g m^{2}$ ， $c = {(l g m)}^{2}$ ，则（）

A、 $a > b > c$ B、 $b > c > a$ C、 $c > a > b$ D、 $c > b > a$

查看试题解析
8. 将函数 $f (x) = sin (2 x + \frac{π}{3})$ 的图象向右平移 $a$ 个单位得到函数 $g (x) = cos 2 x$ 的图象，则 $a$ 的值可以为（）

A、 $\frac{π}{12}$ B、 $\frac{5 π}{12}$ C、 $\frac{11 π}{12}$ D、 $\frac{17 π}{12}$

查看试题解析
9. $6$ 本不同的书摆放在书架的同一层上，要求甲、乙两本书必须摆放在两端，丙、丁两本书必须相邻，则不同的摆放方法有（）种

A、 $24$ B、 $36$ C、 $48$ D、 $60$

查看试题解析
10. 已知函数 $f (x)$ 满足 $f (x + 2) = 2 f (x)$ ，当 $x \in [0 ， 2)$ 时， $f (x) = x$ ，那么 $f (21) =$ （）

A、 $2^{10}$ B、 $2^{11}$ C、 $2^{20}$ D、 $2^{21}$

查看试题解析
11. 已知焦点在 $x$ 轴上的双曲线 $\frac{x^{2}}{m^{2}} - \frac{y^{2}}{m^{2} - 1} = 1$ 的左右两个焦点分别为 $F_{1}$ 和 $F_{2}$ ，其右支上存在一点 $P$ 满足 $P F_{1} ⊥ P F_{2}$ ，且 $Δ P F_{1} F_{2}$ 的面积为3，则该双曲线的离心率为（）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{\sqrt{7}}{2}$ C、 $2$ D、 $3$

查看试题解析
12. 如图是某个四面体的三视图，若在该四面体内任取一点P，则点P落在该四面体内切球内部的概率为（）

A、 $\frac{\sqrt{2}}{9 π}$ B、 $\frac{\sqrt{6} π}{18}$ C、 $\frac{3 \sqrt{2} π}{16}$ D、 $\frac{π}{16}$

查看试题解析

二、填空题

13. 已知 $f (x) = {\begin{array}{l} e^{x} + 1 ， x \leq 0 \\ f (x - 2) ， x > 0 \end{array}$ ，则 $f (3)$ 的值为．

查看试题解析
14. 已知△ABC的内角A，B，C的对边分别为a，b，c，且 $\frac{c o s A}{a} = \frac{c o s C}{2 b - c}$ ，则A=.

查看试题解析
15. 如图，在边长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点P是该正方体对角线 $B D_{1}$ 上的动点，给出下列四个结论：
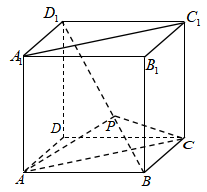
① $A C ⊥ B_{1} P$
② $△ A P C$ 面积的最大值是 $2 \sqrt{3}$
③ $△ A P C$ 面积的最小值是 $\sqrt{2}$
④当 $B P = \frac{2 \sqrt{3}}{3}$ 时，平面 $A C P / /$ 平面 $A_{1} C_{1} D$
其中所有正确结论的序号是.

查看试题解析
16. 已知数列 ${a_{n}}$ 是首项为3，公比为 $q$ 的等比数列， $S_{n}$ 是其前 $n$ 项的和，若 $a_{3} a_{4} + a_{5} = 0$ ，则 $q =$ ； $S_{3} =$ .

查看试题解析

三、解答题

17. 设数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $S_{n} = n^{2} - n$ ，在正项等比数列 ${b_{n}}$ 中， $b_{2} = a_{2}$ ， $b_{4} = a_{5}$ .

(1)、求 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、设 $c_{n} = a_{n} b_{n}$ ，求数列 ${c_{n}}$ 的前n项和.

查看试题解析
18. 某学校在寒假期间安排了“垃圾分类知识普及实践活动”.为了解学生的学习成果，该校从全校学生中随机抽取了50名学生作为样本进行测试，记录他们的成绩，测试卷满分100分，将数据分成6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]，并整理得到频率分布直方图：

(1)、求a的值；

(2)、若全校学生参加同样的测试，试估计全校学生的平均成绩（每组成绩用中间值代替）；

(3)、现将频率视为概率，从全校成绩在80分及以上的学生中随机抽取10人，用X表示其成绩在[90，100]中的人数，求X数学期望及方差.

查看试题解析
19. 如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形， $∠ D A B = \frac{π}{3}$ ， △PAD是以AD为底边的等腰三角形，平面ADP⊥平面ABCD，点E､F分别为PD､BC的中点.

(1)、求证：AE⊥DF；

(2)、当二面角C-EF-D的余弦值为 $\frac{\sqrt{15}}{10}$ 时，求棱PB的长度.

查看试题解析
20. 已知椭圆C的离心率为 $\frac{\sqrt{3}}{2}$ ，长轴的两个端点分别为 $A (- 2 ， 0)$ ， $B (2 ， 0)$ .

(1)、求椭圆C的方程；

(2)、过点 $(1 ， 0)$ 的直线与椭圆C交于M，N（不与A，B重合）两点，直线AM与直线 $x = 4$ 交于点Q，求证： $\frac{S_{△ M B N}}{S_{△ M B Q}} = \frac{| B N |}{| B Q |}$ .

查看试题解析
21. 已知函数 $f (x) = x e^{x} + \frac{\ln x}{x}$ .
（Ⅰ）求证：函数 $f (x)$ 有唯一零点；

（Ⅱ）若对任意 $x \in (0 ， + \infty)$ ， $x e^{x} - \ln x \geq 1 + k x$ 恒成立，求实数 $k$ 的取值范围.

查看试题解析
22. 在直角坐标系xOy中，已知曲线C₁： ${\begin{array}{l} x = c o s α \\ y = s i n^{2} α \end{array}$ (α为参数)，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C₂：ρcos $(θ - \frac{π}{4})$ ＝－ $\frac{\sqrt{2}}{2}$ ，曲线C₃：ρ＝2sin θ.

(1)、求曲线C₁与C₂的交点M的直角坐标；

(2)、设点A，B分别为曲线C₂ ， C₃上的动点，求|AB|的最小值．

查看试题解析
23. 已知函数 $f (x) = | 2 x + 1 | - | x - 1 |$

(1)、解不等式 $f (x) < 2$ .

(2)、若不等式 $| m - 1 | \geq f (x) + | x - 1 | + | 2 x - 3 |$ 有解，求实数 $m$ 的取值范围.

查看试题解析

甲	75	79	82	84	86	87	90	91	93	98
乙	73	81	81	83	87	88	95	96	97	99