湖南省新高考教学教研联盟2022届高三下学期数学4月第二次联考试卷
试卷更新日期:2022-04-20 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、(1) B、 C、 D、2. 已知 , 则( )A、 B、 C、 D、3. 已知圆锥的底面直径为 , 母线长为 , 则其侧面展开图扇形的圆心角为( )A、 B、 C、 D、4. 下列直线中,函数的对称轴是( )A、 B、 C、 D、5. 已知椭圆的左、右焦点分别为、 , 点、均在椭圆上,且均在轴上方,满足条件 , , 则( )A、 B、 C、 D、6. 设 , , 化简( )A、 B、 C、 D、7. 已知 , 如果过点可作曲线的三条切线.则下列结论中正确的是( )A、 B、 C、 D、8. 甲、乙两个质地均匀且完全一样的正方体骰子,每个骰子的六个面上分别标有数字1,2,3,4,5,6.同时抛掷这两个骰子在水平桌面上,记事件为“两个骰子朝上一面的数字之和为奇数”,事件为“甲骰子朝上一面的数字为奇数”,事件为“乙骰子朝上一面的数字为偶数”,则下列结论不正确的是( )A、 B、 C、 D、
二、多选题
-
9. 已知由样本数据组成的一个样本,得到回归直线方程为 , 且 , 去除两个歧义点和后,得到新的回归直线的斜率为3,在下列说法正确的是( )A、相关变量 , 具有正相关关系 B、去除歧义点后,样本的残差为0.1 C、去除歧义点后的回归直线方程为 D、去除歧义点后,随值增加相关变量值增加速度变小10. 设点是的外心,且 , 下列命题为真命题的是( )A、若 , 则 B、若 , 则 C、若是正三角形,则 D、若 , , , 则四边形的面积是11. 正方体的棱长为2,、、分别为、、的中点.则( )
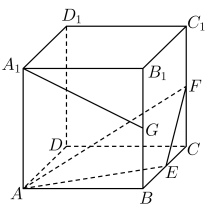 A、直线与直线垂直 B、直线与平面平行 C、平面截正方体所得的截面面积为 D、四面体与四面体的公共部分的体积是12. 已知点在圆上,点 , , 则( )A、点到直线的距离最大值为 B、满足的点有2个 C、过点作圆的两切线,切点分别为、 , 则直线的方程为 D、的最小值是
A、直线与直线垂直 B、直线与平面平行 C、平面截正方体所得的截面面积为 D、四面体与四面体的公共部分的体积是12. 已知点在圆上,点 , , 则( )A、点到直线的距离最大值为 B、满足的点有2个 C、过点作圆的两切线,切点分别为、 , 则直线的方程为 D、的最小值是三、填空题
-
13. 已知函数是奇函数,则.14. 若、是抛物线上的不同两点,弦(不平行于轴)的垂直平分线与轴相交于点 , 则弦中点的横坐标为.15. 函数的极值点为.16. 若在数列的每相邻两项之间插入此两项的积,形成新的数列,再把所得数列按照同样的方法不断构造出新的数列.现对数列1,2进行构造,第一次得到数列1,2,2;第二次得到数列1,2,2,4,2;依次构造,第次得到的数列的所有项的积记为 , 令 , 则 , .
四、解答题
-
17. 已知各项均为正数的数列满足 , , 其中是数列的前项和.(1)、求数列的通项公式;(2)、记 , 求数列的前100项和.18. 3名志愿者在10月1号至10月5号期间参加社区服务工作.(1)、若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;(2)、若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量的分布列.19. 如图,四棱锥中,平面 , 梯形满足 , , 且 , , 为中点, , .
 (1)、求证: , , , 四点共面;(2)、求二面角的正弦值.20. 法国著名军事家拿破仑·波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这个三个三角形的外接圆圆心恰为另一个等边三角形的顶点”.如图,在中,内角 , , 的对边分别为 , , , 已知.以 , , 为边向外作三个等边三角形,其外接圆圆心依次为 , , .
(1)、求证: , , , 四点共面;(2)、求二面角的正弦值.20. 法国著名军事家拿破仑·波拿巴最早提出的一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这个三个三角形的外接圆圆心恰为另一个等边三角形的顶点”.如图,在中,内角 , , 的对边分别为 , , , 已知.以 , , 为边向外作三个等边三角形,其外接圆圆心依次为 , , . (1)、求;(2)、若 , 的面积为 , 求的周长.
(1)、求;(2)、若 , 的面积为 , 求的周长.