河南省名校教研联盟2021-2022学年高三下学期理数3月联考试卷

试卷更新日期：2022-04-20 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = [- 1 ， 3]$ ，集合 $A = {x | l n x < 1}$ ， $B = [- 1 ， 2]$ ，则 $∁_{U} (A ∩ B) =$ （）

A、 $[- 1 ， 0] ∪ (2 ， 3]$ B、 $[- 1 ， 0] ∪ [e ， 3]$ C、 $[- 1 ， 0) ∪ [2 ， 3]$ D、 $[- 1 ， 0] ∪ (2 ， e]$

查看试题解析
2. 已知复数 $z$ 满足 ${(1 - i)}^{2} z = 2 + 2 i$ ，则 $z \cdot \bar{z} =$ （）

A、2 B、0 C、 $- 1 + i$ D、 $2 i$

查看试题解析
3. 某市政府部门为了解该市的“全国文明城市”创建情况，在该市的12个区县市中随机抽查到了甲、乙两县，考核组对他们的创建工作进行量化考核．在两个县的量化考核成绩（均为整数）中各随机抽取20个，得到如图数据（用频率分布直方图估计总体平均数时，每个区间的值均取该区间的中点值）．关于甲乙两县的考核成绩，下列结论正确的是（）

A、甲县平均数小于乙县平均数 B、甲县中位数小于乙县中位数 C、甲县众数不小于乙县众数 D、不低于80的数据个数，甲县多于乙县

查看试题解析
4. 若 $f (x) = (a - \frac{1}{2}) x - \frac{s i n 2 x}{4} + c o s x$ 是R上的减函数，则实数a的取值范围是（）

A、 $[\frac{5}{4} ， + \infty)$ B、 $(- \infty ， - 1]$ C、 $(- \infty ， \frac{5}{4}]$ D、 $[1 ， + \infty)$

查看试题解析
5. 已知 $0 < θ < \frac{π}{4}$ ，设 $a = t a n 2 θ$ ， $b = \frac{c o s 2 θ}{2 (1 - s i n 2 θ)}$ ， $c = s i n 2 θ$ ，则a，b，c的大小关系是（）

A、 $a > b > c$ B、 $b > c > a$ C、 $b > a > c$ D、 $c > a > b$

查看试题解析
6. 已知函数 $f (x) = x c o s x - s i n x$ ，下列结论正确的是（）

A、 $f (x)$ 是以 $2 π$ 为周期的函数 B、0是 $f (x)$ 的极值点 C、 $f (x)$ 是R上的偶函数 D、 $f (x)$ 是区间 $[π ， 2 π]$ 上的增函数

查看试题解析
7. 已知某种袋装食品每袋质量（单位： $g$ ） $X ~ N (500 ， 16)$ ， $P (4 - σ < X \leq 4 + σ) = 0.6827$ ， $P (4 - 2 σ < X \leq 4 + 2 σ) = 0.9545$ ， $P (μ - 3 σ < X \leq μ + 3 σ) = 0.9973$ .则下面结论正确的是（）

A、 $σ = 16$ B、 $P (496 < X \leq 504) = 0.9545$ C、随机抽取10000袋这种食品，每袋质量在区间 $(492 ， 504]$ 的约8186袋 D、随机抽取10000袋这种食品，每袋质量小于 $488 g$ 的不多于14袋

查看试题解析
8. 已知F₁ ， F₂是双曲线C： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a > 0$ ， $b > 0$ ）的两个焦点，C的离心率为5，点 $P (x_{0} ， y_{0})$ 在C上， $\vec{P F_{1}} \cdot \vec{P F_{2}} < 0$ ，则 $x_{0}$ 的取值范围是（）

A、 $(- 3 a ， 3 a)$ B、 $(- 3 a ， - a] ∪ [a ， 3 a)$ C、 $(- \frac{7}{5} a ， \frac{7}{5} a)$ D、 $(- \frac{7}{5} a ， - a] ∪ [a ， \frac{7}{5} a)$

查看试题解析
9. 勾股定理被称为几何学的基石，相传在商代由商高发现，又称商高定理．汉代数学家赵爽利用弦图（又称赵爽弦图，它由四个全等的直角三角形和一个小正方形组成，如图1），证明了商高结论的正确性．现将弦图中的四条股延长相同的长度（如将 $C A$ 延长至 $D$ ）得到图2．在图2中，若 $A D = 5$ ， $B D = 3 \sqrt{10}$ ， $D$ 、 $E$ 两点间的距离为 $\sqrt{145}$ ，则弦图中小正方形的边长为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{2 \sqrt{2}}{3}$ C、1 D、2

查看试题解析
10. 设函数 $f (x) = 2^{s i n α - 1} x^{2} + (2^{- s i n α} - 3) x$ （ $α \in R$ ）图象在点（1， $f (1)$ ）处切线为l，则l的倾斜角 $θ$ 的最小值是（）

A、 $\frac{π}{4}$ B、 $\frac{π}{3}$ C、 $\frac{5 π}{6}$ D、 $\frac{3 π}{4}$

查看试题解析
11. 记数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，已知 $S_{n} = a n^{2} - 4 a n + b$ ，在数集 ${- 1 ， 0 ， 1}$ 中随机抽取一个数作为 $a$ ，在数集 ${- 3 ， 0 ， 3}$ 中随机抽取一个数作为 $b$ .在这些不同数列中随机抽取一个数列 ${a_{n}}$ ，则 ${a_{n}}$ 是递增数列的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{9}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
12. 在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，平面 $A C C_{1} A_{1} ⊥$ 平面 $A B C$ ， $A_{1} A = A_{1} C$ .E，F分别是线段 $A C$ ， $A_{1} B_{1}$ 上的点.下列结论成立的是（）

A、若 $A A_{1} = A C$ ，则存在唯一直线 $E F$ ，使得 $E F ⊥ A_{1} C$ B、若 $A A_{1} = A C$ ，则存在唯一线段 $E F$ ，使得四边形 $A C C_{1} A_{1}$ 的面积 $\frac{2 \sqrt{3}}{3} E F^{2}$ C、若 $A B ⊥ B C$ ，则存在唯一直线 $E F$ ，使得 $E F ⊥ B C$ D、若 $A B ⊥ B C$ ，则存在唯一线段 $E F$ ，使得四边形 $B B_{1} C_{1} C$ 的面积为 $B C \cdot E F$

查看试题解析

二、填空题

13. 已知向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{π}{3}$ ， $| \vec{a} | = 1$ ， $\vec{a} \cdot (\vec{a} + \vec{b}) = 2$ ，则 $| \vec{b} | =$ ．

查看试题解析
14. 在 ${(x - \frac{\sqrt{a}}{\sqrt{x}})}^{8}$ 的展开式中， $x^{5}$ 的系数为28，则a= ．

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} 2^{x - a} ， x \leq 0 \\ 2^{x + a} ， x > 0 \end{array}$ ，关于x的不等式 $f (x) \leq f (2)$ 的解集为I，若 $I$ ⫋ $(- \infty ， 2]$ ，则实数a的取值范围是．

查看试题解析
16. 已知椭圆 $C_{1} ： \frac{x^{2}}{4} + \frac{y^{2}}{b^{2}} = 1 (0 < b < 2)$ 的离心率为 $\frac{1}{2}$ ， $F_{1}$ 和 $F_{2}$ 是 $C_{1}$ 的左右焦点，P是 $C_{1}$ 上的动点，点Q在线段 $F_{1} P$ 的延长线上， $| P Q | = | P F_{2} |$ ，点Q的轨迹为 $C_{2}$ ，线段 $F_{2} Q$ 的垂直平分线交 $C_{2}$ 于A，B两点，则 $| A B |$ 的最小值是.

查看试题解析

三、解答题

17. 已知函数 $y = A s i n (ω x + φ)$ （ $A > 0$ ， $ω > 0$ ， $0 < φ < \frac{π}{2}$ ）的部分图象如图，将该函数图象向右平移 $\frac{π}{12}$ 个单位后，再把所得曲线上的点的横坐标变为原来的2倍（纵坐标不变），得到函数 $f (x)$ 的图象．设 $g (x) = f (x) \cdot s i n x$ ．

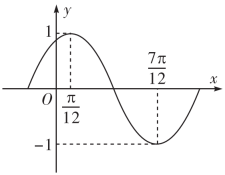(1)、求函数 $g (x)$ 的最小正周期T；

(2)、在三角形ABC中，AB=6，D是BC的中点，AD= $\sqrt{19}$ ，设∠BAC= $θ$ ， $c o s θ < 0$ ， $g (θ) = \frac{\sqrt{3}}{4}$ ，求三角形ABC的面积．

查看试题解析
18. 如图，已知△ABE是正三角形，BC=2AB=2AD=2EF，AD⊥平面ABE，AD∥BC，AD∥EF， $\vec{B C} = 4 \vec{B G}$ ， $\vec{D C} = 4 \vec{D H}$ ．

(1)、求证：平面FGH⊥平面FDC；

(2)、求平面FGD与平面FGH所成锐二面角的余弦值．

查看试题解析
19. 已知抛物线C： $y^{2} = 2 p x$ （ $p > 0$ ）的焦点为F，M（4， $y_{0}$ ）是抛物线C上的点，O为坐标原点， $c o s ∠ O F M = - \frac{3}{5}$ ．

(1)、求抛物线C的方程；

(2)、P（a，b）（ $a \neq 0$ ）为抛物线C上一点，过点P的直线l与圆 ${(x - 3)}^{2} + y^{2} = 1$ 相切，这样的直线l有两条，它们分别交该抛物线C于A，B（异于点P）两点．若直线l的方程为 $x = t y - t b + a$ ，当|PA|=|PB|时，求实数a的值．

查看试题解析
20. 随着中国经济的迅速发展，市场石料需求急增．西部某县有丰富的优质石料，当地政府决定有序开发本县石料资源．因建立石料厂会破坏生态，该县决定石料开发走“开发治理结合，人类生态友好”的路线.当地政府请国家环保机构每年对该县与石料开发相关的生态（以下简称生态）进行评估．若生态开始变差，则下一年石料厂将停产（本问题中，时间以整数年为单位），生态友好后复产．该县在建石料厂之初投入巨资进行与之有关的生态建设，考虑到可持续发展，这种生态投入（以下简称生态投入）将逐年减少 $(4 l n a - a^{2} - 2 a + 10)$ （a是常数， $0 < a < e$ ）亿元．该县从2021年起，若某年生态友好，则下一年生态变差的概率是 $\frac{1}{8}$ ；若某年生态变差，则下一年生态友好的概率为 $\frac{5}{8}$ ．模型显示，生态变差的概率不大于0.16683时，该县生态将不再变差，生态投入结束．

(1)、若2021年该县生态变差的概率为 $\frac{1}{3}$ ，求该县2022年生态友好的概率；

(2)、若2021年该县生态变差概率为 $\frac{1}{3}$ ，生态投入是40亿元，a为何值时，从2021年开始到生态投入结束，对该县总生态投入额最小？并求出其最小值．

查看试题解析
21. 已知 $f (x) = k e^{x} - \frac{1}{2} x^{2}$ ．

(1)、若函数 $f (x)$ 有两个极值点，求实数k的取值范围；

(2)、证明：当 $n \in N^{*}$ 时， $\frac{1}{2^{2}} + \frac{2}{3^{2} e} + \frac{3}{4^{2} e^{2}} + \cdot \cdot \cdot + \frac{n}{{(n + 1)}^{2} e^{n - 1}} < 1$ ．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，已知曲线 $C_{1}$ 的参数方程是 ${\begin{array}{l} x = \sqrt{2} c o s α \\ y = \sqrt{6} s i n α \end{array}$ （ $α$ 为参数），以O为极点，以x轴的正半轴为极轴建立极坐标系，曲线 $C_{2}$ 的极坐标方程是 $ρ = \frac{3 c o s θ}{s i n^{2} θ}$ .

(1)、求曲线 $C_{1}$ 的极坐标方程和曲线 $C_{2}$ 直角坐标方程；

(2)、设曲线 $C_{1}$ 和 $C_{2}$ 交点为A，B，求 $△ O A B$ 的面积.

查看试题解析
23. 已知 $f (x) = \frac{1}{2} | x + 2 | + \frac{1}{2} | x |$ ，直线 $y = a$ 与曲线 $y = f (x)$ 围成的四边形面积为 $S$ ， $0 < S \leq 3$ .

(1)、求实数 $a$ 的取值范围；

(2)、若实数 $b$ ， $c$ 满足 $a + b + c = 3$ ， $a^{2} + b^{2} - c^{2} = 9$ ，求 $c$ 的取值范围.

查看试题解析