河北省保定市2022届高三数学一模试卷
试卷更新日期:2022-04-20 类型:高考模拟
一、单选题
-
1. 已知集合 , 集合 , 则( )A、 B、 C、 D、2. 已知复数 , 复数是复数的共轭复数,则( )A、1 B、 C、2 D、3. 已知 , , , 则a, , c的大小关系为( )A、 B、 C、 D、4. 已知某商品的进价为4元,通过多日的市场调查,该商品的市场销量y(件)与商品售价(元)的关系为 , 则当此商品的利润最大时,该商品的售价x(元)为( )A、5 B、6 C、7 D、85. 已知三棱锥 , 其中平面 , , , 则该三棱锥外接球的表面积为( )A、12π B、16π C、20π D、24π6. 已知函数的图象如图所示,则下面描述不正确的是( )
 A、 B、 C、 D、7. 已知双曲线的右焦点为 , 在右支上存在点P,Q,使得为正方形(为坐标原点),设该双曲线离心率为 , 则( )A、 B、 C、 D、8. 已知函数()图象上存在点M,函数(e为自然对数的底数)图象上存在点N,且M,N关于点对称,则实数a的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知双曲线的右焦点为 , 在右支上存在点P,Q,使得为正方形(为坐标原点),设该双曲线离心率为 , 则( )A、 B、 C、 D、8. 已知函数()图象上存在点M,函数(e为自然对数的底数)图象上存在点N,且M,N关于点对称,则实数a的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 已知向量 , 将向量绕原点逆时针旋转90°得到向量 , 将向量绕原点顺时针旋转135°得到向量 , 则( )A、 B、 C、 D、10. 已知椭圆的左、右焦点分别为 , , 过点的直线与该椭圆相交于 , 两点,点在该椭圆上,且 , 则下列说法正确的是( )A、存在点 , 使得 B、满足为等腰三角形的点有2个 C、若 , 则 D、的取值范围为11. 已知数列的前项和为 , 且满足 , , , 则下面说法正确的是( )A、数列为等比数列 B、数列为等差数列 C、 D、12. 下面描述正确的是( )A、已知 , , 且 , 则 B、函数 , 若 , 且 , 则a+2b的最小值是 C、已知 , 则的最小值为 D、已知 , 则的最小值为
三、填空题
-
13. 若函数在处的切线过点 , 则实数 .14. 2022年北京冬奥会的某滑雪项目中有三个不同的运动员服务点,现需将10名志愿者分配到这三个运动员服务点处,每处需要至少2名至多4名志愿者,则不同的安排方法一共有种.15. 在如图直四棱柱中,底面为菱形, , , 点为棱的中点,若为菱形A1B1C1D1内一点(不包含边界),满足平面 , 设直线与直线所成角为 , 则的最小值为.
 16. 已知定义在上的函数在处取得最小值,则最小值为 , 此时 .
16. 已知定义在上的函数在处取得最小值,则最小值为 , 此时 .四、解答题
-
17. 已知数列的前项和为 , 且 .(1)、求数列的通项公式;(2)、设 , 求的前项和 .18. 如图,在等腰梯形中, , , , 现将沿折起至 , 使得 .
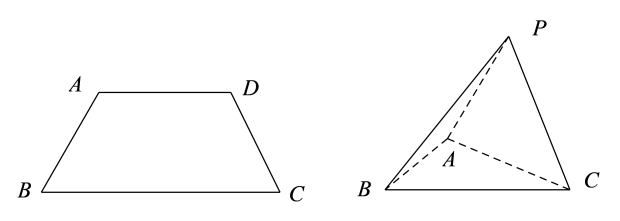 (1)、证明:;(2)、求二面角的余弦值.19. 已知在△中, , 的角平分线与相交于点D.(1)、若 , 求的长;(2)、若 , 求△面积的最小值.20. 2021年初某公司研发一种新产品并投入市场,开始销量较少,经推广,销量逐月增加,下表为2021年1月份到7月份,销量(单位:百件)与月份之间的关系.
(1)、证明:;(2)、求二面角的余弦值.19. 已知在△中, , 的角平分线与相交于点D.(1)、若 , 求的长;(2)、若 , 求△面积的最小值.20. 2021年初某公司研发一种新产品并投入市场,开始销量较少,经推广,销量逐月增加,下表为2021年1月份到7月份,销量(单位:百件)与月份之间的关系.月份x
1
2
3
4
5
6
7
销量y
6
11
21
34
66
101
196
参考数据:
62.14
1.54
2535
50.12
3.47
其中 , .
参考公式:
对于一组数据 , , …, , 其回归直线的斜率和截距的最小二乘估计公式分别为: , .
(1)、画出散点图,并根据散点图判断与(c,d均为大于零的常数)哪一个适合作为销量与月份的回归方程类型(给出判断即可,不必说明理由)? (2)、根据(1)的判断结果及表中的数据,求关于的回归方程,并预测2021年8月份的销量;(3)、考虑销量、产品更新及价格逐渐下降等因素,预测从2021年1月份到12月份(的取值依次记作1到12),每百件该产品的利润为元,求2021年几月份该产品的利润最大.
(2)、根据(1)的判断结果及表中的数据,求关于的回归方程,并预测2021年8月份的销量;(3)、考虑销量、产品更新及价格逐渐下降等因素,预测从2021年1月份到12月份(的取值依次记作1到12),每百件该产品的利润为元,求2021年几月份该产品的利润最大.