贵州省普通高等学校招生2022届高三理数适应性测试试卷

试卷更新日期：2022-04-20 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {x | x^{2} - 2 x \leq 0}$ ， $B = {1 ， 2 ， 3}$ ， $C = {2 ， 3 ， 4}$ ，则 $(A ∩ B) ∪ C =$ （）

A、{2} B、 ${2 ， 3}$ C、 ${1 ， 2 ， 3 ， 4}$ D、 ${0 ， 1 ， 2 ， 3 ， 4}$

查看试题解析
2. 已知复数 $z = (1 - a) + a i$ （ $a \in R$ ），则 $a = 1$ 是 $| z | = 1$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知随机变量X服从正态分布N $(120 ， 5^{2})$ ，若 $P (115 < X < 120) = p$ ，则 $P (X > 125) =$ （）

A、 $1 - p$ B、 $\frac{1 + p}{2}$ C、 $\frac{1 - p}{2}$ D、 $\frac{1 - 2 p}{2}$

查看试题解析
4. 已知 $t a n (α + \frac{π}{4}) = - 3$ ，则 $c o s 2 α =$ （）

A、 $\frac{3}{5}$ B、 $- \frac{3}{5}$ C、 $- \frac{3}{4}$ D、 $\frac{3}{4}$

查看试题解析
5. 如图，在四面体ABCD中，若AB=CB，AD=CD，E是AC的中点，则下列结论正确的是（）

A、平面ABC⊥平面ABD B、平面ABD⊥平面BDC C、平面ABC⊥平面BDE D、平面ABC⊥平面ADC

查看试题解析
6. 设 $O$ 为坐标原点， $F$ 为双曲线 $C$ ： $\frac{x^{2}}{12} - \frac{y^{2}}{b^{2}} = 1$ （ $b > 0$ ）的一个焦点，过 $F$ 作 $C$ 的一条渐近线的垂线，垂足为 $H$ ，则 $| O H | =$ （）

A、 $b$ B、6 C、 $2 \sqrt{3}$ D、 $\sqrt{12 + b^{2}}$

查看试题解析
7. 十七世纪法国数学家费马猜想形如“ $F_{n} = 2^{2^{n}} + 1$ （ $n \in N$ ）”是素数，我们称 $F_{n}$ 为“费马数”．设 $a_{n} = l o g_{2} (F_{n} - 1)$ ， $b_{n} = 2 l o g_{2} a_{n}$ ， $n \in N^{*}$ ，数列 ${a_{n}}$ 与 ${b_{n}}$ 的前n项和分别为 $S_{n}$ 与 $T_{n}$ ，则下列不等关系一定成立的是（）

A、 $a_{n} < b_{n}$ B、 $a_{n} > b_{n}$ C、 $S_{n} \leq T_{n}$ D、 $S_{n} \geq T_{n}$

查看试题解析
8. 如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体的三视图，该几何体外接球的表面积为（）

A、 $4 \sqrt{3} π$ B、 $12 π$ C、 $32 \sqrt{3} π$ D、 $48 π$

查看试题解析
9. 2022年春节期间，G市某天从8~16时的温度变化曲线（如图）近似满足函数 $f (x) = 2 \sqrt{2} c o s (ω x + φ)$ （ $ω > 0$ ， $0 < φ < π$ ， $x \in [8 ， 16]$ ）的图像．下列说法正确的是（）

A、8～13时这段时间温度逐渐升高 B、8～16时最大温差不超过5℃ C、8～16时0℃以下的时长恰为3小时 D、16时温度为−2℃

查看试题解析
10. 函数 $y = f (x)$ 的图像如图，则 $f (x)$ 的解析式可能为（）

A、 $f (x) = (x^{2} - x^{- 2}) l n | x |$ B、 $f (x) = (2^{x} - 2^{- x}) l n | x |$ C、 $f (x) = | 2^{x} - 2^{- x} | l n | x |$ D、 $f (x) = (x^{2} + x^{- 2}) l n | x |$

查看试题解析
11. 已知曲线C₁： $x^{2} = 2 p y$ （ $p > 0$ ）和C₂： ${(x + 1)}^{2} + y^{2} = \frac{5}{16}$ ，点A（−1，y₁）和B（2，y₂）都在C₁上，平行于AB的直线l与C₁ ， C₂都相切，则C₁的焦点为（）

A、（0， $\frac{1}{4}$ ） B、（0， $\frac{1}{2}$ ） C、（0，1） D、（0，2）

查看试题解析
12. 已知函数 $f (x) = \frac{1}{x} + \frac{1}{x - 2} + \frac{1}{x - 4} + 3$ 图像与函数 $g (x) = \frac{2^{x} + 2}{2^{x - 2} + 1}$ 图像的交点为 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ， …， $(x_{m} ， y_{m})$ ，则 $\sum_{i = 1}^{m} (x_{i} + y_{i}) =$ （）

A、20 B、15 C、10 D、5

查看试题解析

二、填空题

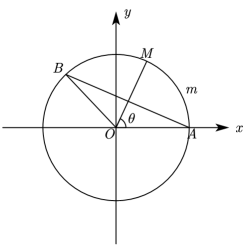
13. （ $2 \sqrt{x} - \frac{1}{\sqrt{x}}$ ）⁶的二项展开式中的常数项为（用数字作答）．

查看试题解析
14. 在平行四边形 $A B C D$ 中， $\vec{A E} = 2 \vec{E D}$ ．若 $\vec{C E} = λ \vec{B A} + μ \vec{B C}$ ，则 $λ + μ =$ ．

查看试题解析
15. 如图，圆O： $x^{2} + y^{2} = 4$ 交x轴的正半轴于点A．B是圆上一点，M是弧 $\overset{⌢}{A m B}$ 的中点，设∠AOM= $θ$ （ $0 < θ < π$ ），函数 $f (θ)$ 表示弦AB长与劣弧 $\overset{⌢}{A M}$ 长之和．当函数 $f (θ)$ 取得最大值时，点M的坐标是．

查看试题解析
16. 将一条线段三等分后，以中间一段为边作正三角形并去掉原线段生成1级Koch曲线“”，将1级Koch曲线上每一线段重复上述步骤得到2级Koch曲线，同理可得3级Koch曲线（如图1），…，Koch曲线是几何中最简单的分形．若一个图形由N个与它的上一级图形相似，相似比为r的部分组成，称 $D = | l o g_{r} N |$ 为该图形分形维数，则Koch曲线的分形维数是．（精确到0.01， $l o g_{3} 2 \approx 0.631$ ）在第24届北京冬奥会开幕式上，一朵朵六角雪花（如图2）飘拂在国家体育场上空，畅想着“一起向未来”的美好愿景．六角雪花曲线是由正三角形的三边生成的三条1级Koch曲线组成，再将六角雪花曲线每一边生成一条1级Koch曲线得到2级十八角雪花曲线（如图3），…，依次得到n级Kn（ $n \in N^{*}$ ）角雪花曲线．若正三角形边长为1，则n级Kn角雪花曲线的周长 $C_{n} =$ ．

查看试题解析

三、解答题

17. 如图，在 $△ A B C$ 中，D是AC边上一点， $∠ A B C$ 为钝角， $∠ D B C = 90 °$ ．

(1)、证明： $c o s ∠ A D B + s i n C = 0$ ；

(2)、若 $A B = 2 \sqrt{7}$ ， $B C = 2$ ，再从下面①②中选取一个作为条件，求 $△ A B D$ 的面积．
① $s i n ∠ A B C = \frac{3 \sqrt{21}}{14}$ ； ② $A C = 3 A D$ ．
注：若选择两个条件分别解答，则按第一个解答计分．

查看试题解析
18. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ ， $G$ ， $H$ 分别是棱 $B B_{1}$ ， $B C$ ， $C D$ ， $D D_{1}$ 的中点．

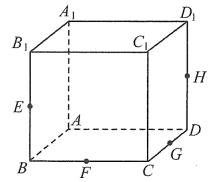(1)、求证： $E$ ， $F$ ， $G$ ， $H$ 四点共面，记过这四点的平面为 $α$ ，在图中画出平面 $α$ 与该正方体各面的交线（不必说明画法和理由）；

(2)、设（1）中平面 $α$ 与该正方体六个面所成锐二面角大小分别为 $θ_{i}$ （ $i$ =1，2，3，4，5，6），求 $\sum_{i = 1}^{6} c o s θ_{i}$ 的值．

查看试题解析
19. 北京冬奥会期间，志愿者团队“Field Cast”从所有参加冬奥会的运动健儿中分别抽取男女运动员各100人的年龄进行统计分析（抽取的运动员年龄均在区间[16，40]内），经统计得出女运动员的年龄频率分布直方图（图1）和男运动员的年龄扇形分布图（图2）．
回答下列问题：

(1)、求图1中的a值；

(2)、利用图2，估计参赛男运动员的平均年龄（同一组中的数据用该组区间的中点值为代表）；

(3)、用分层抽样方法在年龄区间为[16，24）周岁的女运动员中抽取5人，男运动员中抽取4人；再从这9人中随机抽取3人，记这3人中年龄低于20周岁运动员的人数为X，求X的分布列和数学期望．

查看试题解析
20. 如图，椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （ $a > b > 0$ ）的左顶点与上顶点分别为A，B，右焦点为F，点P在C上，PF⊥x轴，AB//OP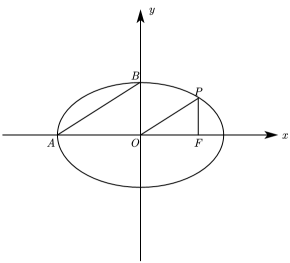， $| A B | = \sqrt{3}$ ．

(1)、求C的方程；

(2)、过F的直线l交椭圆于M，N两点，坐标平面上是否存在定点Q，使得 $\vec{Q M} \cdot \vec{Q N}$ 是定值？若存在，求点Q坐标；若不存在，说明理由．

查看试题解析
21. 已知函数 $f (x) = x l n \frac{x}{e}$ ， $g (x) = a l n x - x^{2} + 1$ ， $e$ 是自然对数的底数．

(1)、求函数 $f (x)$ 的最小值；

(2)、若 $g (x) \leq 0$ 在 $(0 ， + ∞)$ 上恒成立，求实数 $a$ 的值；

(3)、求证： ${(\frac{2023}{2022})}^{2022} < e < {(\frac{2023}{2022})}^{2023}$ ．

查看试题解析
22. 如图，某“京剧脸谱”的轮廓曲线C由曲线C₁和C₂围成．在平面直角坐标系xOy中，C₁的参数方程为 ${\begin{array}{l} x = 3 c o s t \\ y = 3 s i n t \end{array}$ （t为参数，且 $0 \leq t \leq π$ ）．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，C₂的极坐标方程为 $ρ^{2} = \frac{144}{9 + 7 c o s^{2} θ}$ （ $π \leq θ \leq 2 π$ ）．

(1)、求C₁的普通方程和C₂的直角坐标方程；

(2)、已知 $A ， P \in C_{1}$ ， $B \in C_{2}$ ， OA⊥OB．当Rt△OAB的面积最大时，求点P到直线AB距离的最大值．

查看试题解析
23. 已知函数 $f (x) = \sqrt{x - 1} + \sqrt{3 - x} - \frac{1}{2}$ 的定义域为集合D，最大值为m，记 $g (a ， b ， c) = \frac{a}{b + c} + \frac{b}{c + a} + \frac{c}{a + b}$ ，其中a，b，c是正实数．

(1)、求m；

(2)、 $\forall x \in D$ ，求证： $f (x) \leq g (a ， b ， c)$ ．

查看试题解析