北师大版备考2022中考数学二轮复习专题16 等腰、等边及直角三角形
试卷更新日期:2022-04-20 类型:二轮复习
一、单选题
-
1. 如图,上有A、B两点,点C为弧AB上一点,点P是外一点,且 , , 则的度数为( )
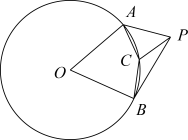 A、 B、 C、 D、2. 如图:等腰中,是上一点,若 , 则( ).
A、 B、 C、 D、2. 如图:等腰中,是上一点,若 , 则( ). A、 B、2 C、1 D、3. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A、 B、2 C、1 D、3. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )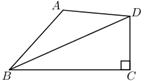 A、24 B、30 C、36 D、424. 如图,在△ABC和△ABD中,AB=AC=AD,AC⊥AD,AE⊥BC于点E,AE的反向延长线于BD交于点F,连接CD.则线段BF,DF,CD三者之间的关系为( )
A、24 B、30 C、36 D、424. 如图,在△ABC和△ABD中,AB=AC=AD,AC⊥AD,AE⊥BC于点E,AE的反向延长线于BD交于点F,连接CD.则线段BF,DF,CD三者之间的关系为( )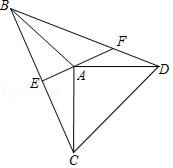 A、BF﹣DF=CD B、BF+DF=CD C、BF2+DF2=CD2 D、无法确定5.
A、BF﹣DF=CD B、BF+DF=CD C、BF2+DF2=CD2 D、无法确定5.如图,在平面直角坐标系 中,已知点 , .若平移点 到点 ,使以点 , , , 为顶点的四边形是菱形,则正确的平移方法是( )
 A、向左平移1个单位,再向下平移1个单位 B、向左平移 个单位,再向上平移1个单位 C、向右平移 个单位,再向上平移1个单位 D、向右平移1个单位,再向上平移1个单位6. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是( )A、 B、24 C、 或24 D、 或247.
A、向左平移1个单位,再向下平移1个单位 B、向左平移 个单位,再向上平移1个单位 C、向右平移 个单位,再向上平移1个单位 D、向右平移1个单位,再向上平移1个单位6. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是( )A、 B、24 C、 或24 D、 或247.在每个小正方形的边长为 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 的另一个格点的运动称为一次跳马变换.例如,在 的正方形网格图形中(如图1),从点 经过一次跳马变换可以到达点 , , , 等处.现有 的正方形网格图形(如图2),则从该正方形的顶点 经过跳马变换到达与其相对的顶点 ,最少需要跳马变换的次数是( )
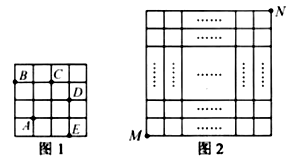 A、 B、 C、 D、8. 如图钓鱼竿AC长6m,露在水面上的鱼线BC长3 m,钓者想看看鱼上钩的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )
A、 B、 C、 D、8. 如图钓鱼竿AC长6m,露在水面上的鱼线BC长3 m,钓者想看看鱼上钩的情况,把鱼竿AC逆时针转动15°到AC′的位置,此时露在水面上的鱼线B'C'长度是( )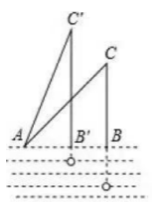 A、3m B、m C、m D、4m9. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A、3m B、m C、m D、4m9. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )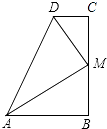 A、30° B、35° C、45° D、60°10. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( )
A、30° B、35° C、45° D、60°10. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( )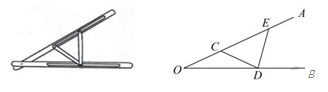 A、60° B、65° C、75° D、80°
A、60° B、65° C、75° D、80°二、填空题
-
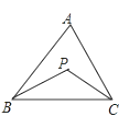
11. 在矩形ABCD中, , , E是BC的中点,连接AE,过点D作于点F,连接CF、AC.(1)、线段DF的长为;(2)、若AC交DF于点M,则 .12. 如图,在△ABC中,∠A=40°,∠ABC与∠ACB的平分线相交于点P,则∠BPC的度数为.
 13. 如图,点P是反比例函数 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= .
13. 如图,点P是反比例函数 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= . (1)、k的值是;(2)、若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是.14.
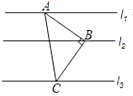
(1)、k的值是;(2)、若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是.14.如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3 . 若l1与l2的距离为4,l2与l3的距离为6,则Rt△ABC的面积为 .
 15. 一副三角板按如图所示叠放在一起,∠C=60°,∠OAB=45°,其中点B,D重合,若固定△AOB,将三角板ACD绕着公共顶点A顺时针旋转一周后停止,当旋转的角度为时,CD∥AO.
15. 一副三角板按如图所示叠放在一起,∠C=60°,∠OAB=45°,其中点B,D重合,若固定△AOB,将三角板ACD绕着公共顶点A顺时针旋转一周后停止,当旋转的角度为时,CD∥AO. 16.
16.如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于 .
 17. 如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为.
17. 如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为. 18. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.
18. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.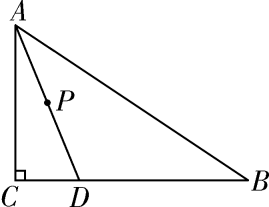 19. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号:
19. 小聪在研究题目“如图,在等腰三角形ABC中, , , 的平分线与AB的垂直平分线OD交于点O,点C沿直线EF折叠后与点O重合,你能得出那些结论?”时,发现了下面三个结论:① ;②图中没有60°的角;③D、O、C三点共线.请你直接写出其中正确的结论序号: 20. 如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2, , . 则△MON 的周长是;
20. 如图,在∠AOB 的边 OA、OB 上取点 M、N,连接 MN,P 是△MON 外角平分线的交点, 若 MN=2, , . 则△MON 的周长是;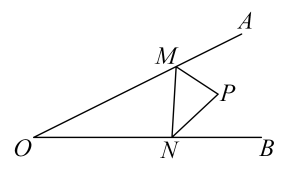
三、作图题
-
21.
已知:如图△ABC .
求作:①AC边上的高BD;
②△ABC的角平分线CE .
 22. 如图,在 Rt△ABC 中,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,试画出所有不同的等腰三角形并说明画图方法.
22. 如图,在 Rt△ABC 中,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,试画出所有不同的等腰三角形并说明画图方法.
四、综合题
-
23.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
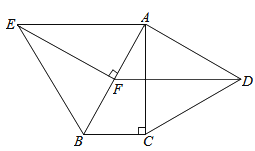 (1)、试说明AC=EF;(2)、求证:四边形ADFE是平行四边形.
(1)、试说明AC=EF;(2)、求证:四边形ADFE是平行四边形.
24. 如图,在中, , , 点D是平面内一动点(不与点C重合),连接CD,将线段CD绕点D顺时针旋转60°,得到线段DE(点E不与点B重合),连接BE.取CD的中点P,连接AP.

 (1)、如图(1),当点E落在线段AC上时,
(1)、如图(1),当点E落在线段AC上时,①;
②直线AP与直线BE相交所成的较小角的度数为 . 请给予证明.
(2)、如图(2),当点E落在平面内其他位置时,(1)中的两个结论是否仍然成立?若成立,请就图(2)的情形给出证明;若不成立,请说明理由.(3)、若 , , 当点B,D,E在同一条直线上时,请直线写出线段AP的长.25.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
 (1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
(1)、试判断直线AB与直线CD的位置关系,并说明理由;(2)、如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.