山东省新泰市2020-2021学年六年级下学期期中检测数学试题
试卷更新日期:2022-04-20 类型:期中考试
一、选择题
-
1. 如图,已知三点A,B,C画直线AB,画射线AC,连接BC,按照上述语句画图正确的是( )A、
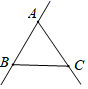 B、
B、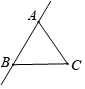 C、
C、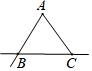 D、
D、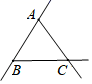 2. 计算:42020×(-0.25)2021=( )A、 B、 C、4 D、-43. 在研制新冠肺炎疫苗中,某细菌的直径大小为0.000 000 000 072米,用科学记数法表示这一数字是( )A、0.72×10-12 B、7.2×10-12 C、7.2×10-11 D、7.2×10-104. 如图1,A、B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小.如图2,连接AB,与l交于点C,则C点即为所求的码头的位置,这样做的理由是( )
2. 计算:42020×(-0.25)2021=( )A、 B、 C、4 D、-43. 在研制新冠肺炎疫苗中,某细菌的直径大小为0.000 000 000 072米,用科学记数法表示这一数字是( )A、0.72×10-12 B、7.2×10-12 C、7.2×10-11 D、7.2×10-104. 如图1,A、B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小.如图2,连接AB,与l交于点C,则C点即为所求的码头的位置,这样做的理由是( )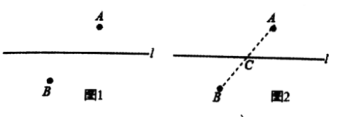 A、经过一点有无数条直线 B、两点确定一条直线 C、两直线相交只有一个交点 D、两点之间,线段最短5. 下列说法正确的个数是( )
A、经过一点有无数条直线 B、两点确定一条直线 C、两直线相交只有一个交点 D、两点之间,线段最短5. 下列说法正确的个数是( )⑴连接两点之间的线段叫两点间的距离;
⑵将线段向两个方向无限延长就形成了直线;
⑶若AB=2CB,则点C是AB的中点:
⑷角的大小与角的两边的长短有关.
A、1个 B、2个 C、3个 D、4个6. 如图,C是AB的中点,D是BC的中点,则下列等式中正确的是( )
①DB=3AD-2AB;②CD=AB;③DB=2AD- AB;④CD=AD-CB.
A、①② B、③④ C、①④ D、②③7. 亲爱的同学们,我们的数学测试从13:30开始,钟表上13时30分时,时针和分针的夹角是( )A、150° B、135° C、130° D、120°8. 南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将下表称为“杨辉三角”(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
则(a+b)8展开式中所有项的系数和是( )
 A、128 B、256 C、512 D、10249. 下列计算正确的是( )A、(2x+y)(3x-y)=6x2-y2 . B、(-x+2y)2=x2-4xy+4y2 . C、(m+n)3(m+n)2=m5+n5 D、(2x-y)2=4x2-xy+y210. 一艘轮船停在海面上,从船上看灯塔的方向在北偏东30°,那么从灯塔看船的方向在( )A、北偏西60° B、南偏西60° C、南偏东30° D、南偏西30°11. 如图所示, 是平角, 是射线, 、 分别是 、 的角平分线,若 ,则 的度数为( )
A、128 B、256 C、512 D、10249. 下列计算正确的是( )A、(2x+y)(3x-y)=6x2-y2 . B、(-x+2y)2=x2-4xy+4y2 . C、(m+n)3(m+n)2=m5+n5 D、(2x-y)2=4x2-xy+y210. 一艘轮船停在海面上,从船上看灯塔的方向在北偏东30°,那么从灯塔看船的方向在( )A、北偏西60° B、南偏西60° C、南偏东30° D、南偏西30°11. 如图所示, 是平角, 是射线, 、 分别是 、 的角平分线,若 ,则 的度数为( )
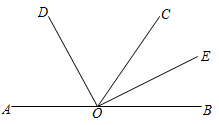 A、56° B、62° C、72° D、124°12. 我们知道下面的结论:若am=an(a>0,且a≠1),则m=n. 设2m=3,2n=6,2p=12.下列关于m,n,p三者之间的关系正确的是( )A、n2-mp=1 B、m+n=2p C、m+p=2n D、p+n=2m
A、56° B、62° C、72° D、124°12. 我们知道下面的结论:若am=an(a>0,且a≠1),则m=n. 设2m=3,2n=6,2p=12.下列关于m,n,p三者之间的关系正确的是( )A、n2-mp=1 B、m+n=2p C、m+p=2n D、p+n=2m二、填空题(本大题共6小题,每小题4分,满分24分)
-
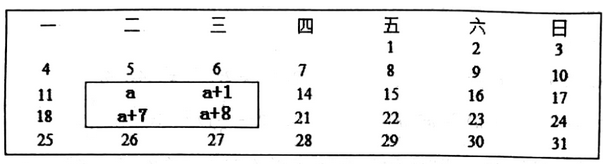
13. 在研究多边形的几何性质时.我们常常把它分割成三角形进行研究.从八边形的一个顶点引对角线,最多把它分割成三角形的个数为14. 代数式49m2-km+1是一个完全平方式,则k的值为15. 计算:(a-b)(-a-b)=16. 在日历上,我们可以发现其中某些数满足一定的规律,如图是2021年1月的日历,我们任意选择其中如图所示的方框部分,将方框部分中4个位置上的数交叉相乘,再相减,结果都是一个常数,这个常数是
 17. 将一个圆分割成四个扇形,使它们的圆心角的度数比为1:2:3:4,则这四个扇形中最大的圆心角的度数为18. 观察下列各式:
17. 将一个圆分割成四个扇形,使它们的圆心角的度数比为1:2:3:4,则这四个扇形中最大的圆心角的度数为18. 观察下列各式:(x-1)(x+1)=x2-1;
(x- 1)(x2+x+1)=x3-1;
(x- 1)(x3+x2+x+1)=x4-1;
从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接填写下面的空格.
32020+32019+……+36+35+34+33+32+3+1=
三、解答题(本大题共7小题,满分78分,解答应写出必要的文字说明、证明过程或推演步骤)
-
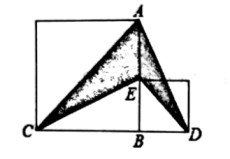
19.(1)、计算:20012-1999×2003;(2)、计算:(3)、已知:xm=3,xn=2,求x2m-3n的值.20. 先化简再求值:(1)、(2x2y)3·(-xy2)+(x4y3),其中,x=;y=2(2)、[(x+2y)2-(3x+y)(-y+3x)-5y2]÷(x),其中(2x+1)2=-|y-2|.21. 如图,大正方形的边长为a,小正方形的边长为b,大正方形与小正方形的面积之差是60,求阴影部分的面积.
 22. 已知(x+a)(x-)的结果中不含x的一次项,求(a+2)2-(1-a)(-a-1)的值.23. 如图,甲、乙都是长方形,边长的数据如图所示(其中m为正整数)。
22. 已知(x+a)(x-)的结果中不含x的一次项,求(a+2)2-(1-a)(-a-1)的值.23. 如图,甲、乙都是长方形,边长的数据如图所示(其中m为正整数)。 (1)、图中的甲长方形的面积S1 , 乙长方形的面积S2 , 试比较S1S2的大小,并说明理由;(2)、现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积S1的差(即S-S1)是一个常数,求出这个常数。24. 如图,已知∠AOB内部有三条射线,若OE平分∠AOD,OC平分∠BOD.
(1)、图中的甲长方形的面积S1 , 乙长方形的面积S2 , 试比较S1S2的大小,并说明理由;(2)、现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S与图中的甲长方形面积S1的差(即S-S1)是一个常数,求出这个常数。24. 如图,已知∠AOB内部有三条射线,若OE平分∠AOD,OC平分∠BOD.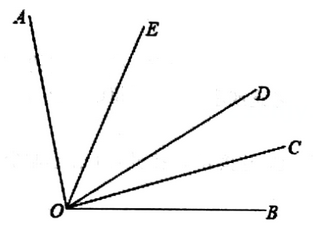 (1)、若∠AOB=100°,求∠EOC的度数;(2)、若∠AOB=70°,如果将题中“平分”的条件改为∠EOA =∠AOD,∠DOC=∠DOB且∠DOE:∠DOC=3:2,求∠EOC的度数.25. 已知:点C在直线AB上,点D、E分别是AC、BC的中点。
(1)、若∠AOB=100°,求∠EOC的度数;(2)、若∠AOB=70°,如果将题中“平分”的条件改为∠EOA =∠AOD,∠DOC=∠DOB且∠DOE:∠DOC=3:2,求∠EOC的度数.25. 已知:点C在直线AB上,点D、E分别是AC、BC的中点。 (1)、当点C在线段AB上时,如图(1),
(1)、当点C在线段AB上时,如图(1),若AC=5,BC=3,则DE= ▲ ;
②若AC+BC=a,你能猜想出DE的长度吗?写出你的猜想并说明理由:
(2)、当点c在线段BA的延长线上,且4C=m, BC=n时,你能猜想出DE的长度吗?(用m,n表示),直接写出你的猜想.