2022年北师大版初中数学七年级下学期期中模拟试题4
试卷更新日期:2022-04-20 类型:期中考试
一、单选题
-
1. 如图是七年级某考生做的水滴入一个玻璃容器的示意图(滴水速度保持不变),能正确反映容器中水的高度( )与时间( )之间对应关系的大致图象是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列计算中错误的是( )A、4a5b3c2÷(﹣2a2bc)2=ab B、(a+1)(a﹣1)(a2+1)=a4﹣1 C、4x2y•(﹣ y)÷4x2y2=﹣ D、25×( x2﹣ x+1)=x2﹣ x+13. 如图,将一个长方形纸条折成如图的形状,若已知 ,则 为( )
2. 下列计算中错误的是( )A、4a5b3c2÷(﹣2a2bc)2=ab B、(a+1)(a﹣1)(a2+1)=a4﹣1 C、4x2y•(﹣ y)÷4x2y2=﹣ D、25×( x2﹣ x+1)=x2﹣ x+13. 如图,将一个长方形纸条折成如图的形状,若已知 ,则 为( ) A、 B、 C、 D、4. 如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定 的个数是( )
A、 B、 C、 D、4. 如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定 的个数是( )① ;② ;③ ;④ .
 A、1 B、2 C、3 D、45. 的计算结果是( )A、 B、 C、 D、6. 有若干个大小形状完全相同的小长方形,现将其中4个如图1摆放,构造出一个正方形,其中阴影部分面积为35;其中5个如图⒉摆放,构造出一个长方形,其中阴影部分面积为102(各个小长方形之间不重叠不留空,则每个小长方形的面积为( )
A、1 B、2 C、3 D、45. 的计算结果是( )A、 B、 C、 D、6. 有若干个大小形状完全相同的小长方形,现将其中4个如图1摆放,构造出一个正方形,其中阴影部分面积为35;其中5个如图⒉摆放,构造出一个长方形,其中阴影部分面积为102(各个小长方形之间不重叠不留空,则每个小长方形的面积为( )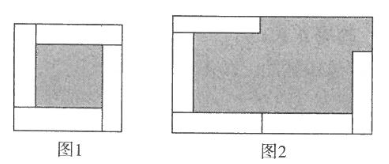 A、4 B、8 C、12 D、167. 如图,已知点 、 、 在同一直线上, , ,则 是( )
A、4 B、8 C、12 D、167. 如图,已知点 、 、 在同一直线上, , ,则 是( ) A、 B、 C、 D、无法确定8. 已知 ,则 的值为( )A、4 B、2 C、-2 D、-4
A、 B、 C、 D、无法确定8. 已知 ,则 的值为( )A、4 B、2 C、-2 D、-4二、填空题
-
9. 如图,在不添加辅助线及字母的前提下,请写出一个能判定 的条件:.
 10. 如图,是汽车加油站在加油过程中加油器仪表某一瞬间的显示,(其中数量用x升表示,金额用y元表示,单价用a元/升表示),结合图片信息,请用适当的方式表示加油过程中变量之间的关系为:.
10. 如图,是汽车加油站在加油过程中加油器仪表某一瞬间的显示,(其中数量用x升表示,金额用y元表示,单价用a元/升表示),结合图片信息,请用适当的方式表示加油过程中变量之间的关系为:. 11. 已知 , ,则 的值为 .12. 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
11. 已知 , ,则 的值为 .12. 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
则当 时,所捂多项式的值是
13. 如图,AB∥CD,∠ABE=148°,FE⊥CD于E,则∠FEB的度数是度.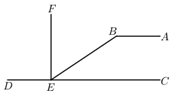 14. 若与的乘积中不含一次项,则m的值为 .15. 如图,将长方形纸片 沿折痕EF折叠,点 , 的对应点分别为点 , , 交 于点 ,再把三角形 沿 折叠,点 的对应点为点 ,若 ,则 的大小是.
14. 若与的乘积中不含一次项,则m的值为 .15. 如图,将长方形纸片 沿折痕EF折叠,点 , 的对应点分别为点 , , 交 于点 ,再把三角形 沿 折叠,点 的对应点为点 ,若 ,则 的大小是.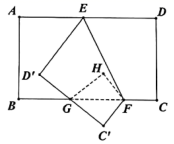 16. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图)就是一例.这个三角形给出了(a+b)n(n=1,2,3,4,5,6)的展开式的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数,等等.
16. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图)就是一例.这个三角形给出了(a+b)n(n=1,2,3,4,5,6)的展开式的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数,等等.有如下四个结论:
①(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
②当a=-2,b=1时,代数式a3+3a2b+3ab2+b3的值是-1;
③当代数式a4+4a3b+6a2b2+4ab3+b4的值是0时,一定是a=-1,b=1;
④(a+b)n的展开式中的各项系数之和为2n.
上述结论中,正确的有(写出序号即可).

三、解答题
-
17.
①先化简,再求值: (a2b-2ab2-b3)÷b-(a-b)(a+b),其中a=-2, .
②若x2+ax+8和多项式x2-3x+b相乘的积中不含x3、x2项,求ab的值.
18. 已知 ,求 的值.19. 完成下面的证明如图,点B在AG上,AGCD,CF平分∠BCD,∠ABE=∠FCB,BE⊥AF点E.
求证:∠F=90°.
证明:∵AGCD(已知)
∴∠ABC=∠BCD( ▲ )
∵∠ABE=∠FCB(已知)
∴∠ABC﹣∠ABE=∠BCD﹣∠FCB
即∠EBC=∠FCD
∵CF平分∠BCD(已知)
∴∠BCF=∠FCD( ▲ )
∴ ▲ =∠BCF(等量代换)
∴BECF( ▲ )
∴ ▲ =∠F( ▲ )
∵BE⊥AF(已知)
∴ ▲ =90°( ▲ )
∴∠F=90°.
 20. 如图,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数.
20. 如图,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数. 21. 如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8dm,r=1.6dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π).
21. 如图所示,小刚家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8dm,r=1.6dm,他想知道剩余阴影部分的面积,你能利用所学过的因式分解的知识帮助小刚计算吗?请写出求解过程(结果保留π). 22.
22.如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到十点为止,哪个人的速度快?
(4)两人最终在几点钟相遇?
(5)你能利用图象中得到的信息,编个故事吗?

四、综合题
-
23. 已知多项式 与另一个多项式 的乘积为多项式 .(1)、若 为关于 的一次多项式 中 的一次项系数为0,直接写出 的值;(2)、若 为 ,求 的值.(3)、若 为关于 的二次多项式 ,判断 是否可能为关于 的三次二项式,如果可能,请求出b,c的值;如果不可能,请说明理由.24. 已知:直线AB∥CD,M,N分别在直线AB,CD上,H为平面内一点,连HM,HN.
 (1)、如图1,延长HN至G,∠BMH和∠GND的角平分线相交于点E.
(1)、如图1,延长HN至G,∠BMH和∠GND的角平分线相交于点E.①若∠BME=25°,∠END=75°,则∠H的度数为 ▲ ;
②探究∠MEN与∠MHN的数量关系,并给予证明;
(2)、如图2,∠BMH和∠HND的角平分线相交于点E.作MP平分∠AMH,NQ∥MP交ME的延长线于点Q,若∠H=150°,求∠ENQ的度数.