广东省佛山市2022届高三数学二模试卷

试卷更新日期：2022-04-19 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 3 ， 1 ， 2}$ ， $B = {x \in N | x^{2} - x - 6 \leq 0}$ ，则 $A ∪ B =$ （）

A、 ${1 ， 2}$ B、 ${- 3 ， 0 ， 1 ， 2}$ C、 ${- 3 ， 1 ， 2 ， 3}$ D、 ${- 3 ， 0 ， 1 ， 2 ， 3}$

查看试题解析
2. 已知函数 $f (x) = s i n ω x (ω > 0)$ 图象上相邻两条对称轴之间的距离为 $\frac{3 π}{2}$ ，则 $ω$ =（）

A、 $\frac{3}{2}$ B、 $\frac{4}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
3. 设x， $y \in R$ ，则“ $x < y$ ”是 $“ (x - y) \cdot y^{2} < 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 核酸检测分析是用荧光定量 $P C R$ 法，通过化学物质的荧光信号，对在 $P C R$ 扩增进程中成指数级增加的靶标 $D N A$ 实时监测，在 $P C R$ 扩增的指数时期，荧光信号强度达到阈值时， $D N A$ 的数量 $X_{n}$ 与扩增次数 $n$ 满足 $\lg X_{n} = n \lg (1 + p) + \lg X_{0}$ ，其中 $p$ 为扩增效率， $X_{0}$ 为 $D N A$ 的初始数量.已知某被测标本 $D N A$ 扩增 $10$ 次后，数量变为原来的 $100$ 倍，那么该样本的扩增效率 $p$ 约为（）
(参考数据： $10^{0.2} \approx 1.585$ ， $10^{- 0.2} \approx 0.631$ )

A、0.369 B、0.415 C、0.585 D、0.631

查看试题解析
5. 如图，某几何体由共底面的圆锥和圆柱组合而成，且圆柱的两个底面和圆锥的顶点均在体积为36π的球面上，若圆柱的高为2，则圆锥的侧面积为（）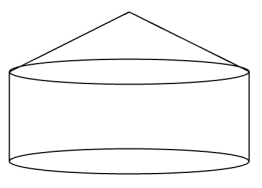

A、2 $\sqrt{6}$ π B、4 $\sqrt{6}$ π C、16π D、 $\frac{16 π}{3}$

查看试题解析
6. 已知双曲线 $E ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 以正方形ABCD的两个顶点为焦点，且经过该正方形的另两个顶点，若正方形ABCD的边长为2，则E的实轴长为（）

A、 $2 \sqrt{2} - 2$ B、 $2 \sqrt{2} + 2$ C、 $\sqrt{2} - 1$ D、 $\sqrt{2} + 1$

查看试题解析
7. 设 $a ， b ， c \in R$ 且 $a \neq 0$ ，函数 $g (x) = a x^{2} + b x + c ， f (x) = (x + 2) g (x)$ ，若 $f (x) + f (- x) = 0$ ，则下列判断正确的是（）

A、 $g (x)$ 的最大值为-a B、 $g (x)$ 的最小值为-a C、 $g (2 + x) = g (2 - x)$ D、 $g (2 + x) = g (- x)$

查看试题解析
8. $△ A B C$ 中， $A B = \sqrt{2} ， ∠ A C B = \frac{π}{4}$ ， O是 $△ A B C$ 外接圆圆心，是 $\vec{O C} \cdot \vec{A B} + \vec{C A} \cdot \vec{C B}$ 的最大值为（）

A、0 B、1 C、3 D、5

查看试题解析

二、多选题

9. 关于复数 $z = c o s \frac{2 π}{3} + i s i n \frac{2 π}{3}$ （i为虚数单位），下列说法正确的是（）

A、 $| z | = 1$ B、 $\bar{z}$ 在复平面上对应的点位于第二象限 C、 $z^{3} = 1$ D、 $z^{2} + z + 1 = 0$

查看试题解析
10. 时代青年李华同学既读圣贤书，也闻窗外事，他关注时政，养成了良好的摘抄习惯，以下内容来自他的摘抄笔记：
过去一年，我们统筹推进疫情防控和经济社会发展，主要做了以下工作：全年国内生产总值增长2.3%；城镇新增就业1186万人，全国城镇调查失业率降到5.2%；年初剩余的551万农村贫困人口全部脱贫；……

今年发展主要预期目标是：国内生产总值增长6%以上；城镇新增就业1100万人以上，城镇调查失业率5.5%左右；居民收入稳步增长；生态环境质量进一步改善，主要污染物排放量继续下降；粮食产量保持在1.3万亿斤以上；……

——摘自李克强总理2021年3月5日政府工作报告

全国总人口为1443497378人，其中：普查登记的大陆31个省、自治区、直辖市和现役军人的人口共1411778724人；香港特别行政区人口为7474200人；澳门特别行政区人口为683218人；台湾地区人口为23561236人；……

——摘自2021年5月11日第七次人口普查公报

过去一年全年主要目标任务较好完成，“十四五”实现良好开局，我国发展又取得新的重大成就；国内生产总值达到114万亿元，增长8.1%；城镇新增就业1269万人，城镇调查失业率平均为5.1%；居民人均可支配收入实际增长8.1%；污染防治攻坚战深入开展，主要污染物排放量维续下降，地级及以上城市细颗粒物平均浓度下降9.1%；粮食产量1.37万亿斤，比上一年增长 $2 %$ ，创历史新高；落实常态化防控举措，疫苗全程接种覆盖率超过85%；……

—摘自李克强总理2022年3月5日政府工作报告

根据以上信息，下列结论正确的有（）

A、2020年国内生产总值不足100万亿元 B、2021年城镇新增就业人数比预期目标增幅超15% C、2020年、2021年粮食产量都超1.3万亿斤 D、2021年完成新冠疫苗全程接种人数约12亿

查看试题解析
11. 在棱长为3的正方体 $A B C D - A_{1} B_{1} C_{1} D$ 中，M是 $A_{1} B_{1}$ 的中点，N在该正方体的棱上运动，则下列说法正确的是（）

A、存在点N，使得 $M N / / B C$ B、三棱锥M— $A_{1} B C_{1}$ 的体积等于 $\frac{9}{4}$ C、有且仅有两个点N，使得MN∥平面 $A_{1} B C_{1}$ D、有且仅有三个点N，使得N到平面 $A_{1} B C_{1}$ 的距离为 $\sqrt{3}$

查看试题解析
12. 已知 $0 < x < y < π$ ，且 $e^{y} s i n x = e^{x} s i n y$ ，其中e为自然对数的底数，则下列选项中一定成立的是（）

A、 $s i n x < s i n y$ B、 $s i n x > s i n y$ C、 $c o s x + c o s y > 0$ D、 $c o s x + c o s y < 0$

查看试题解析

三、填空题

13. 若椭圆 $\frac{x^{2}}{k - 1} + \frac{y^{2}}{3 - k} = 1$ 的焦点在y轴上，则实数k的取值范围是.

查看试题解析
14. 已知sin $(α - \frac{π}{4}) = \frac{\sqrt{2}}{3}$ ，则 $s i n 2 α =$ .

查看试题解析
15. 冬季两项起源于挪威，与冬季狩猎活动有关，是一种滑雪加射击的比赛，北京冬奥会上，冬季两项比赛场地设在张家口赛区的国家冬季两项中心，其中男女混合 $4 \times 6$ 公里接力赛项目非常具有观赏性，最终挪威队惊险逆转夺冠，中国队获得第15名.该项目每队由4人组成（2男2女），每人随身携带枪支和16发子弹（其中6发是备用弹），如果备用弹用完后仍有未打中的残存目标，就按残存目标个数加罚滑行圈数（每图150米），以接力队的最后一名队员到达终点的时间为该队接力的总成绩.根据赛前成绩统计分析某参赛队在一次比赛中，射击结束后，残存目标个数X的分布列如下：
X
0
1
2
3
4
5
6
>6
P
0.15
0.1
0.25
0.2
0.15
0.1
0.05
0
则在一次比赛中，该队射击环节的加罚距离平均为米.

查看试题解析
16. 公比为q的等比数列{ $a_{n}$ }满足： $a_{9} = l n a_{10} > 0$ ，记 $T_{n} = a_{1} a_{2} a_{3} \dots \dots a_{n}$ ，则当q最小时，使 $T_{n} \geq 1$ 成立的最小n值是

查看试题解析

四、解答题

17. 记 $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ， $B = \frac{2 π}{3}$ ，且 $(s i n A + s i n B) s i n C + c o s 2 C = 1$

(1)、求证 $5 a = 3 c$ ；

(2)、若 $△ A B C$ 的面积为 $15 \sqrt{3}$ ，求 $c$ .

查看试题解析
18. 男子冰球比赛上演的是速度与激情的碰撞.2022北京冬奥会男子冰球主要比赛场馆是位于北京奥林匹克公园的“冰之帆”国家体育馆.本届冬奥会男子冰球有12支队伍进入正赛，中国首次组队参赛，比赛规则12支男子冰球参赛队先按照往届冬奥会赛制分成三个小组（每组4个队）.正赛分小组赛阶段与决赛阶段；小组赛阶段各组采用单循环赛制（小组内任两队需且仅需比赛一次）；决赛阶段均采用淘汰制（每场比赛胜者才晋级），先将12支球队按照小组赛成绩进行种子排名，排名前四的球队晋级四分之一决赛（且不在四分之一决赛中遭遇），其余8支球队按规则进行附加赛（每队比赛一次，胜者晋级），争夺另外4个四分之一决赛席位，随后依次是四分之一决赛、半决赛、铜牌幕、金牌赛

(1)、本届冬奥会男子冰球项目从正赛开始到产生金牌，组委会共要安排多少场比赛？

(2)、某机构根据赛前技术统计，率先晋级四分之一决赛的四支球队（甲乙丙丁队）实力相当，假设他们在接下来四分之一决赛、半决赛、铜牌赛、金牌赛中取胜率都依次为 $\frac{3}{4}$ 、 $\frac{1}{2}$ 、 $\frac{1}{2}$ 、 $\frac{1}{2}$ ，且每支球队晋级后每场比赛相互独立，试求甲、乙、丙、丁队都没获得冠军的概率.

查看试题解析
19. 已知数列{ $a_{n}$ }的前n项和为 $S_{n}$ ，且满足 $n S_{n + 1} - (n + 1) S_{n} = n (n + 1) ， n \in N^{*} ， a_{3} = 5$

(1)、求 $a_{1}$ 、 $a_{2}$ 的值及数列{ $a_{n}$ }的通项公式 $a_{n}$ ：

(2)、设 $b_{n} = a_{n} a_{n + 1}$ ，求数列{ $b_{n}$ }的前n项和 $T_{n}$

查看试题解析
20. 如图，在以P，A，B，C，D为顶点的五面体中，平面ABCD为等腰梯形， $A B / / C D ， A D = C D = \frac{1}{2} A B$ ，平面PAD⊥平面PAB， $P A ⊥ P B$ .

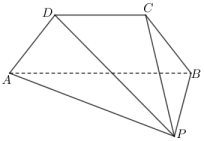(1)、求证：△PAD为直角三角形；

(2)、若 $A D = P B$ ，求直线PD与平面PBC所成角的正弦值.

查看试题解析
21. 已知圆心在x轴上移动的圆经过点A（-4，0），且与x轴、y轴分别交于点B（x，0），C（0，y）两个动点，记点D（x，y）的轨迹为曲线 $Γ$ .

(1)、求曲线 $Γ$ 的方程；

(2)、过点F（1，0）的直线l与曲线 $Γ$ 交于P，Q两点，直线OP，OQ与圆 $F ： {(x - 1)}^{2} + y^{2} = 1$ 的另一交点分别为M，N（其中O为坐标原点），求△OMN与△OPQ的面积之比的最大值.

查看试题解析
22. 已知函数 $f (x) = \frac{- 1 + 2 e^{x}}{2 e^{2 x}} + \frac{x}{a}$ .其中 $e$ 为自然对数的底数.

(1)、当 $a = - \frac{1}{2}$ 时，求 $f (x)$ 的单调区间：

(2)、当 $a > 0$ 时，若 $f (x)$ 有两个极值点 $x_{1} ， x_{2}$ ，且 $f (x_{1}) + f (x_{2}) > k \cdot f (\frac{l n a}{2})$ 恒成立，求 $k$ 的最大值.

查看试题解析

X	0	1	2	3	4	5	6	>6
P	0.15	0.1	0.25	0.2	0.15	0.1	0.05	0