东北三省三校2022届高三理数第二次联合模拟考试试卷

试卷更新日期：2022-04-19 类型：高考模拟

进入出卷网下载

一、单选题

1. 设 $A = {x | y = l o g_{2} (x + 1)}$ ， $B = {x | x^{2} \geq 4}$ ，则 $A ∩ (∁_{R} B) =$ （）

A、 $(- 1 ， 2)$ B、 $[- 1 ， 2)$ C、 $(2 ， + \infty)$ D、 $(- 1 ， + \infty)$

查看试题解析
2. 复数 $z = \frac{4 - 3 i}{2 - i}$ （其中i为虚数单位）的模为（）

A、1 B、 $\sqrt{5}$ C、 $2 \sqrt{5}$ D、5

查看试题解析
3. 已知 ${(2 x - 1)}^{4} + {(x + 1)}^{3} = a_{4} x^{4} + a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ ，则 $a_{2} =$ （）

A、9 B、24 C、27 D、33

查看试题解析
4. 命题“ $\forall x \geq 2$ ， $x^{2} - 4 x + 4 \geq 0$ ”的否定是（）

A、 $\forall x \geq 2$ ， $x^{2} - 4 x + 4 < 0$ B、 $\exists x < 2$ ， $x^{2} - 4 x + 4 < 0$ C、 $\forall x < 2$ ， $x^{2} - 4 x + 4 < 0$ D、 $\exists x \geq 2$ ， $x^{2} - 4 x + 4 < 0$

查看试题解析
5. 为研究变量x，y的相关关系，收集得到下面五个样本点（x，y）：
x
9
9.5
10
10.5
11
y
11
10
8
6
5
若由最小二乘法求得y关于x的回归直线方程为 $\hat{y} = - 3.2 x + \hat{a}$ ，则据此计算残差为0的样本点是（）

A、（9，11） B、（10，8） C、（10.5，6） D、（11.5）

查看试题解析
6. 将函数 $y = s i n (4 x + \frac{π}{6})$ 图象上各点的横坐标伸长为原来的2倍，再向右平移 $\frac{π}{6}$ 个单位，所得图象对应的函数（）

A、在区间 $(0 ， \frac{π}{3})$ 上单调递增 B、在区间（ $- \frac{π}{6}$ ， $\frac{π}{12}$ ）上单调递减 C、图象关于点（ $\frac{π}{3}$ ， 0）对称 D、图象关于直线 $x = \frac{π}{12}$ 对称

查看试题解析
7. 盒子中装有编号为0，1，2，3，4，5，6的7个球，从中任意取出两个，则这两个球的编号之和为3的倍数的概率为（）

A、 $\frac{4}{21}$ B、 $\frac{5}{21}$ C、 $\frac{2}{7}$ D、 $\frac{1}{3}$

查看试题解析
8. 已知圆锥的顶点为点S，底面圆心为点O，高是底面半径r的 $\sqrt{2}$ 倍，点A，B是底面圆周上的两点，若△SAB是等边三角形，则O到平面SAB的距离为（）

A、 $\frac{1}{3} r$ B、 $\frac{\sqrt{2}}{3} r$ C、 $\frac{\sqrt{7}}{3} r$ D、 $\frac{2 \sqrt{2}}{3} r$

查看试题解析
9. 若 $t a n (\frac{π}{4} - x) = 2 t a n (\frac{π}{4} + x)$ ，则 $s i n 2 x =$ （）

A、 $- \frac{3}{5}$ B、 $\frac{3}{5}$ C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
10. 定义域为R的奇函数 $f (x)$ 满足 $f (x) = f (- x + 2)$ ，当 $x \in (0 ， 1]$ 时， $f (x) = x + l o g_{2} (5 x)$ ，则 $f (\frac{2022}{5}) =$ （）

A、 $\frac{7}{5}$ B、 $- \frac{3}{5}$ C、 $\frac{2}{5}$ D、0

查看试题解析
11. 已知实数 $a ， b ， c$ 满足 $a < 2$ ， $a l n a - 2 l n 2 = a - 2$ ， $b < \sqrt{2}$ ， $b l n b - \sqrt{2} l n \sqrt{2} = b - \sqrt{2}$ ， $c > \frac{1}{2}$ ， $c l n c - \frac{1}{2} l n \frac{1}{2} = c - \frac{1}{2}$ ，则（）

A、 $c < b < a$ B、 $b < c < a$ C、 $a < c < b$ D、 $a < b < c$

查看试题解析
12. 我们常说函数 $y = \frac{1}{x}$ 的图象是双曲线，建立适当的平面直角坐标系，可求得这个双曲线的标准方程为 $\frac{x^{2}}{2} - \frac{y^{2}}{2} = 1$ ．函数 $y = \frac{x}{\sqrt{3}} + \frac{\sqrt{3}}{x}$ 的图象也是双曲线，在适当的平面直角坐标系中，它的标准方程可能是（）

A、 $\frac{x^{2}}{6} - \frac{y^{2}}{2} = 1$ B、 $\frac{x^{2}}{6} - \frac{y^{2}}{18} = 1$ C、 $\frac{x^{2}}{7} - \frac{y^{2}}{\frac{7}{3}} = 1$ D、 $\frac{x^{2}}{7} - \frac{y^{2}}{21} = 1$

查看试题解析

二、填空题

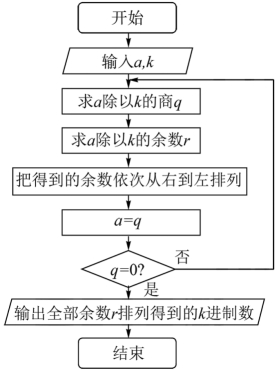
13. 在爱尔兰小说《格列佛游记》里，有格列佛在小人国一顿吃了1728份小人饭的叙述，作者为什么要使用这么复杂的数字呢？许多研究者认为，之所以选用这个数字，跟英国人计数经常使用的十二进制有关系．中国文化中，十二进制也有着广泛应用，如12地支，12个时辰，12生肖…．十二进制数通常使用数字0—9以及字母A，B表示，其中A即数字10，B即数字11．对于下面的程序框图，若输入a=1728，k=12，则输出的数为．

查看试题解析
14. 在正六边形 $A B C D E F$ 中，点 $G$ 为线段 $D F$ （含端点）上的动点，若 $\vec{C G} = λ \vec{C B} + μ \vec{C D}$ （ $λ$ ， $μ \in R$ ），则 $λ + μ$ 的取值范围是．

查看试题解析
15. 椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （ $a > b > 0$ ）的左焦点为点F，过原点O的直线与椭圆交于P，Q两点，若∠PFQ=120°， $| O F | = \sqrt{3}$ ， $| O P | = \sqrt{7}$ ，则椭圆C的离心率为．

查看试题解析
16. 如图，多面体ABCDEF中，面ABCD为正方形，DE⊥平面ABCD，CF∥DE，且AB=DE=2，CF=1，G为棱BC的中点，H为棱DE上的动点，有下列结论：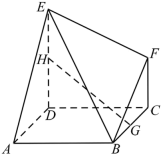
①当H为DE的中点时，GH∥平面ABE；
②存在点H，使得GH⊥AE；
③三棱锥B−GHF的体积为定值；
④三棱锥E−BCF的外接球的表面积为 $14 π$ ．
其中正确的结论序号为．（填写所有正确结论的序号）

查看试题解析

三、解答题

17. 如图，正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $B A = B B_{1} = 2$ ，点D是棱 $A A_{1}$ 的中点．

(1)、求证： $B D ⊥ B_{1} C$ ；

(2)、求二面角 $B - D C - B_{1}$ 的余弦值．

查看试题解析
18. 近期，国家出台了减轻义务教育阶段学生作业负担和校外培训负担“双减”政策．为了坚决落实“双减”政策，提高教学质量，提升课后服务水平，某中心小学计划实行课后看护工作．现随机抽取该中心小学三年级的10个班级并调查了解需要课后看护的学生人数，如下面频数分布表：
班级代号
1
2
3
4
5
6
7
8
9
10
需看护学生人数
20
18
27
30
24
23
32
35
21
20
已知该中心小学每个班级50人，为了节约资源并保证每个看护教室有两名看护教师，该校计划：若需要课后看护的学生人数超过25人的班级配备1名班主任和1名其他科任教师；若需要课后看护的学生人数不超过25人的班级只配备1名班主任，但需要和另一个人数不超过25人的班级合班看护．

(1)、若将上述表格中人数不超过25人的6个班两两组合进行课后看护，求班级代号为1，2的两个班合班看护的概率；

(2)、从已抽取的10个班级中随机抽取3个班，记3个班中需要课后看护的学生人数超过25人的班级数为X，求X的分布列及数学期望．

查看试题解析
19. 已知等差数列 ${a_{n}}$ 公差不为零， $a_{1} + a_{2} + a_{3} = a_{5}$ ， $a_{2} \cdot a_{3} = a_{8}$ ，数列 ${b_{n}}$ 各项均为正数， $b_{1} = 1$ ， $b_{n}^{2} - 3 b_{n + 1}^{2} = 2 b_{n} b_{n + 1}$ ．

(1)、求数列 ${a_{n}}$ ， ${b_{n}}$ 的通项公式；

(2)、若 $\frac{λ}{b_{n + 1}} + 6 \geq a_{n}$ 恒成立，求实数 $λ$ 的最小值．

查看试题解析
20. 已知函数 $f (x) = a x e^{x} - {(x + 1)}^{2}$ （ $a \in R$ ， e为自然对数的底数）．

(1)、若 $f (x)$ 在x=0处的切线与直线y=ax垂直，求a的值；

(2)、讨论函数 $f (x)$ 的单调性；

(3)、当 $a \geq \frac{1}{e^{2}}$ 时，求证： $f (x) \geq l n x - x^{2} - x - 2$ ．

查看试题解析
21. 已知点F为抛物线E： $y^{2} = 2 p x$ （ $p > 0$ ）的焦点，点P（−3，2）， $| P F | = 2 \sqrt{5}$ ，若过点P作直线与抛物线E顺次交于A，B两点，过点A作斜率为1的直线与抛物线的另一个交点为点C．

(1)、求抛物线E的标准方程；

(2)、求证：直线BC过定点；

(3)、若直线BC所过定点为点Q，△QAB，△PBC的面积分别为S₁ ， S₂ ，求 $\frac{S_{1}}{S_{2}}$ 的取值范围

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，以原点为极点， $x$ 轴正半轴为极轴建立极坐标系，点 $A ， B$ 的极坐标分别为 $A (2 ， \frac{5 π}{4}) ， B (2 ， \frac{π}{4})$ ，圆 $C_{1}$ 以 $A B$ 为直径，直线 $l$ 的极坐标方程为 $ρ c o s (θ + \frac{π}{4}) = 6$ ．

(1)、求圆 $C_{1}$ 及直线 $l$ 的直角坐标方程；

(2)、圆 $C_{1}$ 经过伸缩变换 ${\begin{array}{l} x^{'} = \frac{\sqrt{2}}{2} x \\ y^{'} = \frac{\sqrt{6}}{2} y \end{array}$ 得到曲线 $C_{2}$ ，已知点 $P$ 为曲线 $C_{2}$ 上的任意一点，求点 $P$ 到直线 $l$ 距离的取值范围．

查看试题解析
23. 已知函数 $f (x) = | 2 x - 1 | - | 2 x + 1 |$ 的值域为 $M = [a ， b]$ ．

(1)、若 $x \in M$ ， $y \in M$ ，求证： $x^{2} y^{2} + 16 \geq 4 x^{2} + 4 y^{2}$ ；

(2)、若 $| y + a z | < 2$ ， $| b y + z | < 1$ ，求证： $| z | < 1$ ．

查看试题解析

班级代号	1	2	3	4	5	6	7	8	9	10
需看护学生人数	20	18	27	30	24	23	32	35	21	20

x	9	9.5	10	10.5	11
y	11	10	8	6	5