2022年北师大版初中数学七年级下学期期中模拟试题3

试卷更新日期：2022-04-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 ${(- 2 a^{2} b)}^{3} = - 8 a^{6} b^{3}$ B、 $a^{6} \div a^{3} + a^{2} = 2 a^{2}$ C、 $2 a + 3 b = 5 a b$ D、 $a^{2} \cdot a^{4} = a^{8}$

查看试题解析
2. 如图所示，把AB，CD，EF三根木条钉在一起，使之可以在连结点M，N处自由旋转，若∠1=50°，∠2=60°，则如何旋转木条AB才能使它与木条CD平行.
小明说：把木条AB绕点M逆时针旋转10°

小刚说：把木条AB绕点M顺时针旋转170°.

以下说法中正确的是（）

A、小明的操作正确，小刚的操作错误 B、小明和小刚的操作都正确 C、小明的操作错误，小刚的操作正确 D、小明和小刚的操作都错误

查看试题解析
3. 若 $(m x + 3) (x^{2} - x - n)$ 的运算结果中不含 $x^{2}$ 项和常数项，则m，n的值分别为（）

A、 $m = 0$ ， $n = 0$ B、 $m = 0$ ， $n = 3$ C、 $m = 3$ ， $n = 1$ D、 $m = 3$ ， $n = 0$

查看试题解析
4. 如图，AB//DE，∠1=∠2，则AE与DC的位置关系是（）

A、相交 B、平行 C、垂直 D、无法确定

查看试题解析
5. 根据科学研究表明，在弹簧的承受范围内，弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的重量x（kg）间有下表的关系：下列说法不正确的是（）

x/kg

0

1

2

3

4

5

y/cm

20

20.5

21

21.5

22

22.5

A、弹簧不挂重物时的长度为0cm B、x与y都是变量，且x是自变量，y是因变量 C、随着所挂物体的重量增加，弹簧长度逐渐变长 D、所挂物体的重量每增加1kg，弹簧长度增加0.5cm

查看试题解析
6. 某工厂去年底积压产品a件(a＞0)，今年预计每月销售产品2b件(b＞0)，同时每月可生产出产品b件，则产品积压量y(件)与今年开工时间t(月)的关系的图象应是（）

A、 B、 C、 D、

查看试题解析
7. 如图有两张正方形纸片A和B ，图1将B放置在A内部，测得阴影部分面积为2，图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为20，若将3个正方形A和2个正方形B并列放置后构造新正方形如图3，（图2，图3中正方形AB纸片均无重叠部分）则图3阴影部分面积（）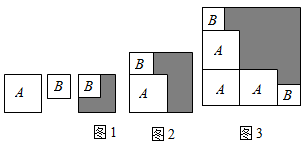

A、22 B、24 C、42 D、44

查看试题解析
8. 如图，AB $/ /$ CD，∠ABE＝ $\frac{1}{2}$ ∠EBF，∠DCE＝ $\frac{1}{3}$ ∠ECF，设∠ABE＝α，∠E＝β，∠F＝γ，则α，β，γ的数量关系是（）

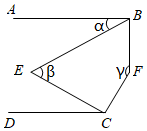A、4β﹣α+γ＝360° B、3β﹣α+γ＝360° C、4β﹣α﹣γ＝360° D、3β﹣2α﹣γ＝360°

查看试题解析

二、填空题

9. 长方形的面积为 $x^{2} - 2 x y + x$ ，其中一边长是 $x$ ，则另一边长是．

查看试题解析
10. 如图所示，直尺一边BC与量角器的零刻度线AD平行，若量角器的一条刻度线OE的读数为65°，OE与BC交于点F，那么∠BFE=.

查看试题解析
11. 如图，某计算装置有一数据输入口A和一运算结果的输出口B，如表是小明输入的一些数据和这些数据经该装置计算后输出的相应结果按照这个计算装置的计算规律，若输入的数是n，则输出的数是.

A 1 2 3 4 5

B 2 5 10 17 26

查看试题解析
12. 已知2^x＝a，则2^x•4^x•8^x＝（用含a的代数式表示）.

查看试题解析
13.
如图，在我国南宋数学家杨辉所著的《解：九章算术》一书中，介绍了展开式的系数规律，称为“杨辉三角”.如第5行的5个数是1，4，6，4，1，恰好对应着 ${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$ 展开式中的各项系数.利用上述规律计算： $10 1^{4} - 4 \times 10 1^{3} + 6 \times 10 1^{2} - 4 \times 101 =$ .
$\begin{array}{l} {(a + b)}^{0} 1 \\ {(a + b)}^{1} 1 1 \\ {(a + b)}^{2} 1 2 1 \\ {(a + b)}^{3} 1 3 3 1 \\ {(a + b)}^{4} 1 4 6 4 1 \\ {(a + b)}^{5} 1 5 10 10 5 1 \\ \dots \dots \dots \dots \end{array}$

查看试题解析
14. 阅读理解：如果一个数的平方等于﹣1，记为i²＝﹣1，i叫做虚数单位，我们把形如a+bi（a、b为实数，且b≠0）的数叫做复数，其中a叫这个复数的实部，b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
如：（4+i）+（6﹣2i）＝（4+6）+（1﹣2）i＝10﹣i；

（2﹣i）（3+i）＝2×3+2i﹣3i﹣i²＝6﹣i﹣（﹣1）＝7﹣i.

根据以上信息，计算（3+i）（1﹣3i）＝.

查看试题解析
15. 如果一个角的两边与另一个角的两边分别平行，那么这两个角的关系是.

查看试题解析
16. 若 $a = 2017 x + 2018$ ， $b = 2017 x + 2019$ ， $c = 2017 x + 2020$ ，则 $a^{2} + b^{2} + c^{2} - a b - a c$ $- b c =$ ．

查看试题解析

三、解答题

17. 如图，已知AB∥CD，∠A=60°，∠ECD=120°，求∠ECA的度数.

查看试题解析
18. 先化简，再求值：（x+2）²+（2x+1）（2x﹣1）﹣4x（x+1），其中x＝﹣1

查看试题解析
19. 已知：如图， $∠ 1 = ∠ C$ ， $∠ 2 + ∠ 3 = 180 °$ .
求证： $A D$ ∥ $E F$ .

查看试题解析

四、综合题

20. 如图，直线AB，CD相交于点O， $∠ F O D = 90 °$ ， OF平分 $∠ A O E$ .

(1)、写出图中所有与 $∠ A O D$ 互补的角；

(2)、若 $∠ A O E = 120 °$ ，求 $∠ B O D$ 的度数.

查看试题解析
21. 如图，从边长为a的正方形纸片中剪掉一个边长为b的正方形纸片（如图1），然后将剩余部分拼成一个长方形（如图2）．

(1)、探究：上述操作能验证的等式是．

(2)、应用：利用（1）中得出的等式，计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \cdot \cdot \cdot (1 - \frac{1}{9^{2}}) (1 - \frac{1}{10^{2}})$ ．

查看试题解析

22. 某小型加工厂2020年的年产值是15万元，计划以后每年增加2万元.

(1)、写出年产值

y

（万元）与经过的年数

x

之间的关系式：

(2)、填写表格中

y

的对应值：

年数 $x$	0	1	2	3	4	5	……
$y$ （万元）	15						……

(3)、求5年后的年产值.

查看试题解析

23. 完全平方公式： ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 适当的变形，可以解决很多的数学问题.
例如：若 $a + b = 3 ， a b = 1$ ，求 $a^{2} + b^{2}$ 的值.
解：因为 $a + b = 3 ， a b = 1$
所以 ${(a + b)}^{2} = 9 ， 2 a b = 2$
所以 $a^{2} + b^{2} + 2 a b = 9 ， 2 a b = 2$
得 $a^{2} + b^{2} = 7$ .
根据上面的解题思路与方法，解决下列问题：

(1)、若 $x + y = 8 ， x^{2} + y^{2} = 40$ ，求 $x y$ 的值；

(2)、若 $(4 - x) (5 - x) = 8$ ，则 $(4 - x)^{2} + {(5 - x)}^{2} =$ ；

(3)、如图，点 $C$ 是线段 $A B$ 上的一点，以 $A C 、 B C$ 为边向两边作正方形，设 $A B = 6$ ，两正方形的面积和 $S_{1} + S_{2} = 18$ ，求图中阴影部分面积.

查看试题解析
24. 已知AM $∥$ CN，点B在直线AM、CN之间，AB⊥BC于点B．

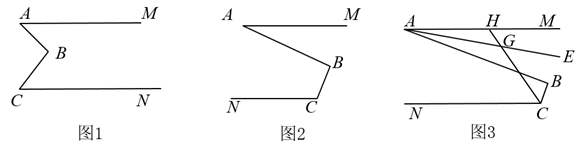(1)、如图1，请直接写出∠A和∠C之间的数量关系：．

(2)、如图2，∠A和∠C满足怎样的数量关系？请说明理由．

(3)、如图3，AE平分∠MAB，CH平分∠NCB，AE与CH交于点G，则∠AGH的度数为．

查看试题解析

x/kg	0	1	2	3	4	5
y/cm	20	20.5	21	21.5	22	22.5