四川省南充市蓬安县2021年中考数学模拟试卷（3月）

试卷更新日期：2022-04-19 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2021的倒数为（）

A、﹣ $\frac{1}{2021}$ B、 $\frac{1}{2021}$ C、﹣2021 D、2021

查看试题解析
2. 下列运算正确的是（）

A、a³•a²＝a⁵ B、a³+a²＝a⁵ C、（a³）²＝a⁵ D、a⁶÷a³＝a²

查看试题解析
3. 习近平总书记提出精准扶贫战略以来，各地积极推进精准扶贫，加大帮扶力度，全国脱贫人口数不断增加.2020年最后一批脱贫人口约5510000人，将数据5510000用科学记数法表示为（）

A、5.51×10² B、0.551×10³ C、5.51×10⁷ D、5.51×10⁶

查看试题解析
4. 如图， $l_{1} ∥ l_{2}$ ，点O在直线l₁上，且∠AOB=90°，若∠2=51°，则∠1的度数为（）

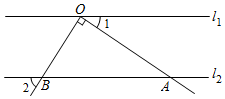A、51° B、49° C、39° D、29°

查看试题解析
5. 将分别标有“精”“准”“扶”“贫”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其它差别，每次摸球前先搅拌均匀，随机摸出一球，放回后；再随机摸出一球，两次摸的球上的汉字组成词语“扶贫”的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{6}$ C、 $\frac{1}{8}$ D、 $\frac{1}{16}$

查看试题解析
6. 在⊙O中，直线l交⊙O于A、B两点，若弦AB长16cm，将直线l向下平移4cm后就与⊙O相切，则⊙O的半径长为（）cm.

A、12 B、10 C、8 D、6

查看试题解析
7. 某农场挖一条480米的渠道，开工后，每天比原计划多挖20米，结果提前4天完成任务，若设原计划每天挖x米，那么下列方程正确的是（）

A、 $\frac{480}{x} - \frac{480}{x + 20} = 4$ B、 $\frac{480}{x} - \frac{480}{x + 4} = 20$ C、 $\frac{480}{x - 20} - \frac{480}{x} = 4$ D、 $\frac{480}{x - 4} - \frac{480}{x} = 20$

查看试题解析
8. 如图，在边长为2的菱形ABCD中，∠B＝30°，过点A作AE⊥BC于点E，若现将△ABE沿直线AE翻折至△AFE的位置，设AF与CD交于点G，则 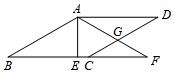$\frac{D G}{C G}$ 等于（）

A、 $\frac{\sqrt{3} - 1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3} + 1}{2}$

查看试题解析
9. 设[m）表示大于m的最小整数，如[5.5）＝6，[﹣1.2）＝﹣1，则下列结论中正确的是（）

A、[2）﹣2＝0 B、若[m）﹣m＝0.5，则m＝0.5 C、[m）﹣m的最大值是1 D、[m）﹣m的最小值是0

查看试题解析
10. 二次函数y＝ax²＋bx＋c的图象如图所示，下列四个结论中：①a＋b＋c＞0；②a﹣b＋c＜0；③abc＞0；④5a﹣b＋c＜0，其中正确的结论有（）个.

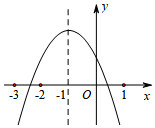A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 因式分解：x³﹣4xy²= ．

查看试题解析
12. 若x，y为实数，且满足|2x＋1|＋ $\sqrt{9 + 2 y}$ =0，则x＋y的值为.

查看试题解析
13. 一组数据1，2，m，4的方差为 $\frac{3}{2}$ ，则m的值为.

查看试题解析
14. 若反比例函数 $y = (k + 1) x^{k^{2} - 5}$ 的图象在第二、四象限内，则 $k =$ .

查看试题解析
15. 在矩形ABCD中，AB＝2，BC＝2AB，E是AB上的一点，沿CE将△EBC上翻折，若B点恰好落在边AD上的F点，则AF＝.

查看试题解析
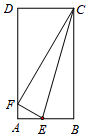16. 如图，在菱形MNEF中，∠NMF=60°，动点A在对角线ME上，点B是NE边的中点，设AM的长度为x，AN＋AB=y，变量y是变量x的函数，当变量x取最大值时，函数y有对应值为9，当变量x=m时，函数y有对应最小值为n，则m＋n的值为.

查看试题解析

三、解答题

17. 计算： $(\frac{1}{4})^{- 1} - (\sqrt{2} - 3 \sqrt{3})^{0} - | 3 - π | + (- 1^{2})$ .

查看试题解析
18. 如图，在△ABC和△DCB中，∠A＝∠D＝90°，AC＝BD，AC与BD相交于点O.

(1)、求证：△ABC≌△DCB；

(2)、△OBC是何种三角形？证明你的结论.

查看试题解析
19. 小王随机调查了某社区40位老人每周参加户外体育锻炼活动的时间情况，根据调查统计结果绘制了频数分布直方图，根据图中信息回答下列问题：

(1)、求a的值；

(2)、从时间在6～10小时的几位老人中随机选取2人，请你用列举法或画树状图法，求其中至少有1人户外体育锻炼活动的时间在8～10小时的概率.

查看试题解析
20. 已知关于x的一元二次方程x²﹣（2m﹣2）x+（m²﹣2m）=0．

(1)、求证：方程有两个不相等的实数根．

(2)、如果方程的两实数根为x₁ ， x₂ ，且x₁²+x₂²=10，求m的值．

查看试题解析
21. 如图，直线y=kx＋b的图象与双曲线 $y = \frac{m}{x}$ 的图象交于A(1，3)，B(-3，n)两点.

(1)、求反比例函数和一次函数的解析式；

(2)、根据图象直接写出一次函数的值小于反比例函数的值的x的取值范围；

(3)、求△AOB的面积.

查看试题解析
22. 如图，AB是⊙O的直径，C、D在圆上，且AC＝DC，过C点的切线CE和DB的延长线交于E点，⊙O的半径r＝5，CD＝8

(1)、求证：BC平分∠ABE；

(2)、求证：CE⊥DE；

(3)、求DE的长.

查看试题解析
23. 本次初二模拟考试后，学校决定购买两种笔记本对模拟考试中的成绩优异、进步显著的同学进行奖励.计划购买甲、乙两种型号的笔记本共60本，已知甲型笔记本的单价为15元/本，而购买乙型笔记本所需总费用y（元）与购买数量 $x$ （本）之间存在如图所示的数量关系.

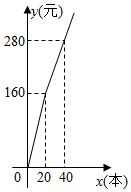(1)、求y与 $x$ 的函数关系式；

(2)、若计划购买一种笔记本的数量不超过40本，但不少于总数的 $\frac{1}{5}$ ，请设计购买方案，使购买总费用最低，并求出最低费.

查看试题解析
24. 在平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AB，点E、F分别是OA、BC的中点，连接BE、EF.

(1)、求证：EF= $\frac{1}{2}$ BC；

(2)、在上述条件下，若AC=BD，G是BD上一点，且BG：GD=3：1，连接EG、FG，试判断四边形EBFG的形状，并证明你的结论.

查看试题解析
25. 如图，抛物线y=ax²＋bx＋c与x轴分别交于点A、B，与y轴交于点C，OB=6，顶点D(2，8)，对称轴交x轴于点Q.

(1)、求抛物线的解析式；

(2)、点P是抛物线的对称轴上一动点，以点P为圆心的圆经过A、B两点，当⊙P与直线CD相切时，求P的坐标；

(3)、动点M在对称轴上运动时，是否存在△DCM和△BQC相似？如果存在，求出点M的坐标；如果不存在，请说明理由.

查看试题解析