四川省绵阳市游仙区2021年九年级中考数学一诊试卷

试卷更新日期：2022-04-19 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列国产车的标志中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 关于x的方程（m﹣1）x²＋x＋m²＋2m﹣3＝0的一个根是0，则m的值是（）

A、7 B、﹣3 C、1或﹣3 D、0

查看试题解析
3. 某口罩加工厂今年一月口罩产值达80万元，第一季度总产值达340万元，问二，三月份的月平均增长率是多少？设月平均增长率的百分数为x，则由题意可得方程为（）

A、80（1+x）²＝340 B、80+80（1+x）²＝340 C、80（1+x）+80（1+x）²＝340 D、80+80（1+x）+80（1+x）²＝340

查看试题解析
4. 将抛物线y＝x²﹣4x﹣4向左平移3个单位，再向上平移3个单位，得到抛物线的表达式为（）

A、y＝（x+1）²﹣13 B、y＝（x﹣5）²﹣5 C、y＝（x﹣5）²﹣13 D、y＝（x+1）²﹣5

查看试题解析
5. 如图，在△ABC中，将△ABC绕着点A顺时针旋转后，得到△AB′C′，且点C′在BC上，若∠B′C′B＝52°，则∠C的度数为（）

A、74° B、66° C、64° D、76°

查看试题解析
6. 如图，ABCDEF是中心为原点O，顶点 $A$ ， D在 $x$ 轴上，半径为4的正六边形，则顶点F的坐标为（）

A、 $(2 ， 2 \sqrt{3})$ B、 $(- 2 ， 2)$ C、 $(- 2 ， 2 \sqrt{3})$ D、 $(- 1 ， \sqrt{3})$

查看试题解析
7. 如图，A、B、C三点在⊙O上，若∠ACB＝∠AOB，则∠AOB的度数是（）

A、60° B、90° C、100° D、120°

查看试题解析
8. 某鱼塘里养了1600条鲤鱼，若干条草鱼和800条鲢鱼，该鱼塘主通过多次捕捞试验后发现，捕到草鱼的频率稳定在0.5附近，则该鱼塘捞到鲢鱼的概率约为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
9. 如图，矩形ABCD的边长 $A B = 1$ ， $B C = 2$ .把BC绕 $B$ 逆时针旋转，使 $C$ 恰好落在AD上的点 $E$ 处，线段BC扫过部分为扇形 $B C E$ .若扇形BCE正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是 $($ $)$

A、 $\frac{1}{6}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{2}{3}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析
10. 已知二次函数y＝ax²+bx+c与自变量x的部分对应值如表，下列说法错误的是（）
x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…

A、a＜0 B、方程ax²+bx+c＝﹣2的正根在4与5之间 C、2a+b＞0 D、若点（5，y₁）、（﹣ $\frac{3}{2}$ ， y₂）都在函数图象上，则y₁＜y₂

查看试题解析
11. 如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G.若BG＝4，CG＝3，则CE的长为（）

A、5 $\frac{2}{7}$ B、5 C、5 $\frac{1}{11}$ D、 $\sqrt{26}$

查看试题解析
12. 如图，函数y₁＝|x²﹣m|的图象如图，坐标系中一次函数y₂＝x＋b的图象记为y₂ ，则以下说法中：①当m＝1，且y₁与y₂恰好有三个交点时b有唯一值为1；②当m＝4，且y₁与y₂只有两个交点时，b＞ $\frac{17}{4}$ 或﹣2＜b＜2；③当m＝﹣b时，y₁与y₂一定有交点：④当m＝b时，y₁与y₂至少有2个交点，且其中一个为（0，m）.正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 平面直角坐标系中，P（x，2＋y）与Q（2y，x）关于原点对称，则xy＝.

查看试题解析
14. 如图，在一次游园活动中，数学小组制作了一面“赵爽弦图锣”，其中 $∠ A B C = 90 °$ ， $A C = 50 c m$ ， $A B = 30 c m$ ，小明蒙上眼睛用棍子击中了锣面，他击中阴影部分的概率是.

查看试题解析
15. 飞机着陆后滑行的距离s（单位：米）与滑行的时间t（单位：秒）之间的函数关系式是s＝96t﹣1.2t² ，那么飞机着陆后秒停下.

查看试题解析
16. 已知△ABC三边的长分别为5、12、13，那么△ABC内切圆的半径为.

查看试题解析
17. 若min{a，b，c}表示a，b，c三个数中的最小值，当y＝min{x² ， 2x＋4，12﹣x}时，则y的取值范围是.

查看试题解析
18. 等边△ABC的边长为6，P是AB上一点，AP＝2，把AP绕点A旋转一周，P点的对应点为P′，连接BP′，BP′的中点为Q，连接CQ.则CQ长度的最小值是.

查看试题解析

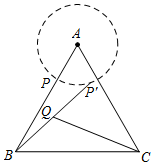
三、解答题

19. 解方程：x²＋2x＋1＝3x＋3

查看试题解析
20. 在乐善中学组织的体育测试中，小壮掷出的实心球的高度 $y (m)$ 与水平距离 $x (m)$ 之间的关系式是 $y = - \frac{1}{10} (x - 3)^{2} + \frac{5}{2}$ ，求小壮此次实心球推出的水平距离.

查看试题解析

21. 疫情期间，游海中学进行了一次线上数学学情调查，九（1）班数学李老师对成绩进行分析，制作如下的频数分布表和频数分布直方图.60到70之间学生成绩尚未统计，根据情况画出的扇形图如图.请解答下列问题：

类别	分数段	频数（人数）
A	$60 \leq x < 70$	a
B	$70 \leq x < 80$	16
C	$80 \leq x < 90$	24
D	$90 \leq x < 100$	6

(1)、完成频数分布表，a= ▲ ， B类圆心角= ▲ °，并补全频数分布直方图；

(2)、全校九年级共有720名学生全部参加此次测试，估计该校成绩

80 \leq x < 100

范围内的学生有多少人？

(3)、九（1）班数学老师准备从D类优生的6人中随机抽取两人进行线上学习经验交流，已知这6人中有两名是无家长管理的留守学生，求恰好只选中其中一名留守学生进行经验交流的概率.

查看试题解析

22. 如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（2，4）、B（1，2）、C（5，3）.以点（0，0）为旋转中心，将△ABC顺时针旋转90°，得到△A₁B₁C₁

(1)、在坐标系中画出△A₁B₁C₁

(2)、若△ABC上有一点P（m，n），直接写出旋转后对应点P₁的坐标.

(3)、求旋转中线段AC所经过部分的面积.

查看试题解析
23. 已知关于x的一元二次方程（a﹣3）x²﹣4x+3＝0有两个不等的实根.

(1)、求a的取值范围；

(2)、当a取最大整数值时，△ABC的三条边长均满足关于x的一元二次方程（a﹣3）x²﹣4x+3＝0，求△ABC的周长.

查看试题解析
24. 如图，游仙怡心月季养植园是一个矩形ABCD，AD＝32米，AB＝20米.为了便于养护与运输，养植园内留有四横四纵等宽道路，养植面积与道路面积比为7：3

(1)、求道路的宽度.

(2)、养植区域内月季盆裁要均匀摆放，即每平方米摆放的盆数一样.每平方米最多能摆放36盆，密度越大，花的品质会下降，每盆月季的出售价也会随之降低.大棚内现在每平米有月季小盆栽10盆，每盆的出售价为5元.分析发现：每平方米每增加5盆，每盆的出售价会下降0.5元.老板准备增加养植数量，以获得最多的出售总额，那么每平米应该养植多少盆月季小盆栽才能使出售总额最多？

查看试题解析
25. 如图1，O是△ABC的边BC的中点，⊙O与BC交于E、F两点，与AB相切于点D，连接AO交⊙O于点P， $\overset{⌢}{E P} = \overset{⌢}{F P}$ .

(1)、猜想AC与⊙O的位置关系，并证明你的猜想.

(2)、如图2，延长AO交⊙O于Q点，连接DE、DF，DQ，FQ，FQ＝ $\frac{13 \sqrt{2}}{2}$ ， ED＝5，求DQ的长.

(3)、如图3，若DE＝5，连接DF、DP、PF，设DP＝x，△DPF的面积为y，求y与x之间的函数关系式.

查看试题解析
26. 如图，抛物线y＝ax²＋bx＋c与x轴交于A（1，0），B（5，0）两点，与y轴交于点C.抛物线顶点纵坐标为﹣4

(1)、求抛物线的解析式及C点坐标.

(2)、如图1，过C作x轴的平行线，与抛物线交于点M，连接AM、BM，在y轴上是否存在点N，使∠ANB＝∠AMB？若存在，请求出点N的坐标；若不存在，请说明理由.

(3)、把线段OC绕O点顺时针旋转，使C点恰好落在抛物线对称轴上的点P处，如图2，再将线段OP绕P点逆时针旋转45°得线段PQ，请计算Q点坐标，并判断Q点在抛物线上吗？

查看试题解析

x	…	﹣1	0	1	3	…
y	…	﹣3	1	3	1	…