四川省绵阳市涪城区2021年中考数学一诊试卷
试卷更新日期:2022-04-19 类型:中考模拟
一、单选题
-
1. 下列各项是一元二次方程的是( )A、x﹣x3=1 B、2x﹣1=a C、x2﹣x+1=0 D、x2﹣=52. 下列手机手势解锁图案中,是中心对称图形的是( )A、
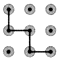 B、
B、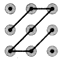 C、
C、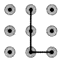 D、
D、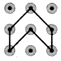 3. 将抛物线y=x2平移得到抛物线y=(x+2)2+3,下列叙述正确的是( )A、向右平移2个单位,向上平移3个单位 B、向左平移2个单位,向上平移3个单位 C、向右平移2个单位,向下平移3个单位 D、向左平移2个单位,向下平移3个单位4. 风力发电是一种绿色可持续的能源获取方式,我国近年来在西部地区大力发展风电产业,如图的风力发电转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
3. 将抛物线y=x2平移得到抛物线y=(x+2)2+3,下列叙述正确的是( )A、向右平移2个单位,向上平移3个单位 B、向左平移2个单位,向上平移3个单位 C、向右平移2个单位,向下平移3个单位 D、向左平移2个单位,向下平移3个单位4. 风力发电是一种绿色可持续的能源获取方式,我国近年来在西部地区大力发展风电产业,如图的风力发电转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( ) A、60 B、90 C、120 D、1505. 方程x2﹣3x﹣1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为( )
A、60 B、90 C、120 D、1505. 方程x2﹣3x﹣1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为( )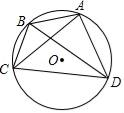 A、50° B、60° C、70° D、80°7. 某校初2017级学生毕业时,每一位同学都将自己的照片向全班其他同学各送一张留作纪念,某班共送了1892张照片,设全班有名学生,根据题意,列出方程应为( )A、 B、 C、 D、8. 如图,⊙O1的直径AB长度为12,⊙O2的直径为8,∠AO1O2=30°,⊙O2沿直线O1O2平移,当⊙O2平移到与⊙O1和AB所在直线都有公共点时,令圆心距O1O2=x,则x的取值范围是( )
A、50° B、60° C、70° D、80°7. 某校初2017级学生毕业时,每一位同学都将自己的照片向全班其他同学各送一张留作纪念,某班共送了1892张照片,设全班有名学生,根据题意,列出方程应为( )A、 B、 C、 D、8. 如图,⊙O1的直径AB长度为12,⊙O2的直径为8,∠AO1O2=30°,⊙O2沿直线O1O2平移,当⊙O2平移到与⊙O1和AB所在直线都有公共点时,令圆心距O1O2=x,则x的取值范围是( )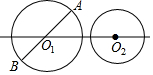 A、2≤x≤10 B、4≤x≤16 C、4≤x≤4 D、2≤x≤89. 如图,C、D是抛物线y=x2﹣x﹣3上在x轴下方的两点,且CD//x轴,过点C、D分别向x轴作垂线,垂足分别为B、A,则矩形ABCD周长的最大值为( )
A、2≤x≤10 B、4≤x≤16 C、4≤x≤4 D、2≤x≤89. 如图,C、D是抛物线y=x2﹣x﹣3上在x轴下方的两点,且CD//x轴,过点C、D分别向x轴作垂线,垂足分别为B、A,则矩形ABCD周长的最大值为( )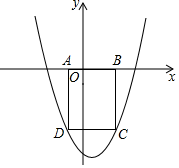 A、 B、 C、 D、10. 如图,AB是⊙O的直径,C为⊙O上的点,把AOC沿OC对折,点A的对应点D恰好落在⊙O上,且C、D均在直径AB上方,连接AD、BD,若AC=4 , BD=4,则AD的长度应是( )
A、 B、 C、 D、10. 如图,AB是⊙O的直径,C为⊙O上的点,把AOC沿OC对折,点A的对应点D恰好落在⊙O上,且C、D均在直径AB上方,连接AD、BD,若AC=4 , BD=4,则AD的长度应是( )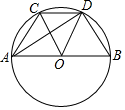 A、12 B、10 C、8 D、611. 如图,⊙O的半径是4,A为⊙O上一点,M是⊙A上一点(M在⊙O内),过点M作⊙A切线l,且l与⊙O相交于P,Q两点,若⊙A的半径为2,当线段PQ最长时线段OM的长度为m,当线段PQ最短时线段OM的长度为n,则m﹣n的值是( )
A、12 B、10 C、8 D、611. 如图,⊙O的半径是4,A为⊙O上一点,M是⊙A上一点(M在⊙O内),过点M作⊙A切线l,且l与⊙O相交于P,Q两点,若⊙A的半径为2,当线段PQ最长时线段OM的长度为m,当线段PQ最短时线段OM的长度为n,则m﹣n的值是( )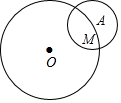 A、2﹣3 B、 C、2﹣2 D、2﹣212. 已知P1(x1 , y1),P2(x2 , y2),…,Pn(xn,yn),…是二次函数y=x2﹣2x+1图象上的一系列点,其中x1=1,x2=2,…,xn=n,…,记A1=x1+y2 , A2=x2+y3 , …,An=xn+yn+1(n为正整数),令S=+…+ , 则S的值是( )A、 B、 C、 D、
A、2﹣3 B、 C、2﹣2 D、2﹣212. 已知P1(x1 , y1),P2(x2 , y2),…,Pn(xn,yn),…是二次函数y=x2﹣2x+1图象上的一系列点,其中x1=1,x2=2,…,xn=n,…,记A1=x1+y2 , A2=x2+y3 , …,An=xn+yn+1(n为正整数),令S=+…+ , 则S的值是( )A、 B、 C、 D、二、填空题
-
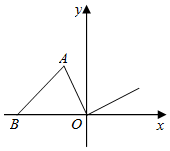
13. 抛物线的顶点坐标为.14. 已知关于x的一元二次方程x2+bx﹣2=0的一个根为1,则它的另一根为.15. 如图,在平面直角坐标系xOy中,以原点O为旋转中心,将△AOB顺时针旋转90°得到△A′OB′,其中点A′与点A对应,点B′与点B对应.若点A(﹣1,2),B(﹣3,0),则直线A′B′的解析式为.
 16. 如图,抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C,在其对称轴上有一动点M,连接MA、MC、AC,则当△MAC的周长最小时,点M的坐标是.
16. 如图,抛物线与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C,在其对称轴上有一动点M,连接MA、MC、AC,则当△MAC的周长最小时,点M的坐标是.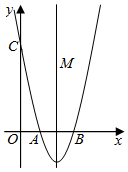 17. 如图,在平面直角坐标系xOy中,一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,点P在线段AB上,⊙P与x轴交于A、C两点,当⊙P与y轴相切时,AC的长度是.
17. 如图,在平面直角坐标系xOy中,一次函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,点P在线段AB上,⊙P与x轴交于A、C两点,当⊙P与y轴相切时,AC的长度是.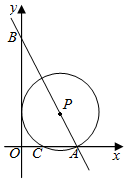 18. 抛物线y=ax2+bx+c经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示,对于此抛物线有如下四个结论:①ac>0;②9a+3b+c>0;③若m>n>0,则x=1+m时的函数值大于x=1﹣n时的函数值;④点(﹣ , 0)一定在此抛物线上.其中正确结论的序号是(填写所有正确结论的序号).
18. 抛物线y=ax2+bx+c经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示,对于此抛物线有如下四个结论:①ac>0;②9a+3b+c>0;③若m>n>0,则x=1+m时的函数值大于x=1﹣n时的函数值;④点(﹣ , 0)一定在此抛物线上.其中正确结论的序号是(填写所有正确结论的序号).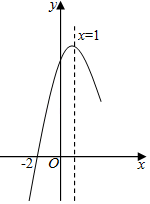
三、解答题
-
19. 解方程(1)、x2+10x+9=0;(2)、3x(2x+1)=4x+2.20. 若关于x的方程x2+2x+k﹣1=0有实数根.(1)、求k的取值范围;(2)、当k取得最大整数值时,求此时方程的根.21. 如图,直角三角形ABC中,∠ABC=90°,D为AB上一点,以BD为直径作⊙O,CD与⊙O交于点E,延长AE与BC交于点F,且CF=BF.
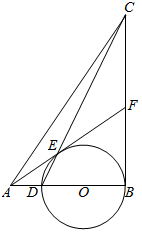 (1)、求证:AF与⊙O相切;(2)、若AB=8,BC=12,求⊙O半径.22. 某农户欲通过电商平台销售自家农产品,已知这种产品的成本价为元/千克.通过市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)大致有如下关系:
(1)、求证:AF与⊙O相切;(2)、若AB=8,BC=12,求⊙O半径.22. 某农户欲通过电商平台销售自家农产品,已知这种产品的成本价为元/千克.通过市场调查发现,该产品每天的销售量(千克)与销售价(元/千克)大致有如下关系:.设这种产品每天的销售利润为(元).
(1)、当销售价定为多少元时,每天的销售利润最大?最大利润是多少?(2)、如果物价部门规定这种产品的销售价不得高于元/千克,该农户想要每天获得元的销售利润,销售价应定为多少元?23. 如图,在平面直角坐标系xOy中,抛物线y=﹣x2+2x+3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,抛物线顶点为点D.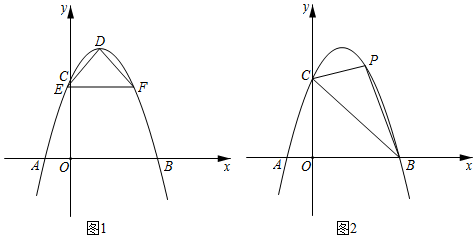 (1)、求B,C,D三点坐标;(2)、如图1,抛物线上有E,F两点,且EF//x轴,当△DEF是等腰直角三角形时,求线段EF的长度;(3)、如图2,连接BC,在直线BC上方的抛物线上有一动点P,当△PBC面积最大时,点P坐标.24. 如图,在平面直角坐标系xOy中,A为第一象限中的点,M、D为x轴正半轴上动点,点O与点D关于点M对称,将射线MA绕点M旋转后得到射线MB,且∠AMB=∠AOM,作AC⊥AM与射线MB交于点C,连接CD.
(1)、求B,C,D三点坐标;(2)、如图1,抛物线上有E,F两点,且EF//x轴,当△DEF是等腰直角三角形时,求线段EF的长度;(3)、如图2,连接BC,在直线BC上方的抛物线上有一动点P,当△PBC面积最大时,点P坐标.24. 如图,在平面直角坐标系xOy中,A为第一象限中的点,M、D为x轴正半轴上动点,点O与点D关于点M对称,将射线MA绕点M旋转后得到射线MB,且∠AMB=∠AOM,作AC⊥AM与射线MB交于点C,连接CD.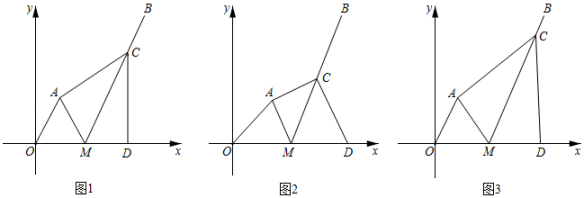 (1)、如图1,当△OAM是等边三角形时,求证:CD⊥OD;(2)、如图2,若点A(1,1),OM= , 求CD长度;(3)、如图3,若点A(1,2),MB//OA,求点C的坐标.25. 如图,在平面直角坐标系中,抛物线与y轴交点为 , 对称轴为 , 点P为第一象限中抛物线上的点,A、B分别为x轴,y轴上点,且四边形是正方形.
(1)、如图1,当△OAM是等边三角形时,求证:CD⊥OD;(2)、如图2,若点A(1,1),OM= , 求CD长度;(3)、如图3,若点A(1,2),MB//OA,求点C的坐标.25. 如图,在平面直角坐标系中,抛物线与y轴交点为 , 对称轴为 , 点P为第一象限中抛物线上的点,A、B分别为x轴,y轴上点,且四边形是正方形.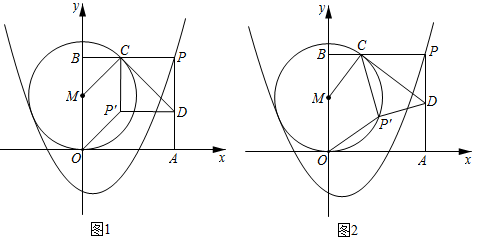 (1)、求抛物线解析式;(2)、若点M为y轴正半轴上的点,与x轴相切,与边交于点C,过点C作的切线与边交于点D,将沿对折得到;
(1)、求抛物线解析式;(2)、若点M为y轴正半轴上的点,与x轴相切,与边交于点C,过点C作的切线与边交于点D,将沿对折得到;①如图1,是否存在点M,使得四边形为平行四边形,若存在请求出的面积,若不存在请说明理由;
②如图2,当点恰好落在上时,求点M坐标.