广西壮族自治区玉林市玉州区2020-2021学年八年级下学期期中数学试卷

试卷更新日期：2022-04-19 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{2^{2}}$ 的值为（）

A、2 B、4 C、±2 D、 $\pm \sqrt{2}$

查看试题解析
2. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{0.4}$ C、 $\sqrt{7}$ D、 $\sqrt{\frac{2 b}{2}}$

查看试题解析
3. 平行四边形的一个内角是70°，则其他三个角是（）

A、70°，130°，130° B、110°，70°，120° C、110°，70°，110° D、70°，120°，120°

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{(- 2) \times (- 3)} = \sqrt{- 2} \times \sqrt{- 3}$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
5. 如图，菱形 $A B C D$ 中， $∠ D = 130 °$ ，则 $∠ 1 =$ （）

A、 $30 °$ B、 $25 °$ C、 $20 °$ D、 $15 °$

查看试题解析
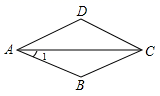6. 如图，点E在正方形ABCD的边AB上，若EB＝1，EC＝2，那么正方形ABCD的面积为（）

A、 $\sqrt{3}$ B、3 C、 $\sqrt{5}$ D、5

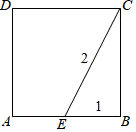查看试题解析
7. 如图：一个长、宽、高分别为4cm、3cm、12cm的长方体盒子能容下的最长木棒长为（　　）

A、11cm B、12cm C、13cm D、14cm

查看试题解析
8. 如图，点O是矩形ABCD的对角线AC的中点，M是CD边的中点.若AB=8，OM=3，则线段OB的长为（　　）

A、5 B、6 C、8 D、10

查看试题解析
9. 如图，在给定的一张平行四边形纸片上按如下操作：连结AC，作AC的垂直平分线MN分别交AD、AC、BC于M、O、N，连结AN，CM，则四边形ANCM是（）

A、矩形 B、菱形 C、正方形 D、无法判断

查看试题解析
10. 实数 $a$ 在数轴上的位置如图所示，则化简 $\sqrt{{(a - 4)}^{2}} + \sqrt{{(a - 11)}^{2}}$ 结果为（　　）

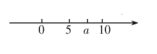A、7 B、-7 C、 $2 a - 15$ D、无法确定

查看试题解析
11. 如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a，较短直角边长为b，大正方形面积为S₁ ，小正方形面积为S₂ ，则（a+b）²可以表示为（）

A、S₁﹣S₂ B、S₁+S₂ C、2S₁﹣S₂ D、S₁+2S₂

查看试题解析
12. 如图，在菱形 $A B C D$ 中， $∠ D = 135 °$ ， $A D = 6 \sqrt{2}$ ， $C E = 4$ ，点P是线段 $A C$ 上一动点，点F是线段 $A B$ 上一动点，则 $P E + P F$ 的最小值（）

A、 $4 \sqrt{2}$ B、6 C、 $2 \sqrt{10}$ D、 $4 \sqrt{5}$

查看试题解析

二、填空题

13. 化简： $\sqrt{8}$ =

查看试题解析
14. 在平行四边形 $A B C D$ 中，若 $∠ A = 50 °$ ，则 $∠ C =$ .

查看试题解析
15. 已知一个三角形的三边分别是6cm、8cm、10cm ，则这个三角形的面积是．

查看试题解析
16. 若 $\sqrt{45 n}$ 是整数，则正整数n的最小值是．

查看试题解析
17. 在平面直角坐标系中有两点 $A (- 3 ， 5)$ ， $B (1 ， 2)$ ， A，B两点间的距离是.

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ， D、E为 $B C$ 上两点， $∠ D A E = 45 °$ ， F为 $△ A B C$ 外一点，且 $F B ⊥ B C$ ， $F A ⊥ A E$ ，则下列结论：① $C E = B F$ ；② $B D^{2} + C E^{2} = D E^{2}$ ；③ $S_{△ A D E} ＝ \frac{1}{4} A D \cdot E F$ ；④ $C E^{2} + B E^{2} = 3 A E^{2}$ ，其中正确的是（写代号）.

查看试题解析

三、解答题

19. 计算： $\sqrt{12} \div \sqrt{\frac{1}{3}} + \sqrt{18} - \sqrt{8}$ .

查看试题解析
20. 已知 $x = \sqrt{2} + 1$ ， $y = \sqrt{2} - 1$ ，求下列各式的值：

(1)、 $x^{2} + 2 x y + y^{2}$ ；

(2)、 $x^{2} - y^{2}$ .

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ 于点D， $A B = \sqrt{8}$ ， $B C = \sqrt{2}$ ，求 $C D$ 的长.

查看试题解析
22. 如图，平行四边形 $A B C D$ 中，对角线 $B D$ 平分 $∠ A B C$ .求证：平行四边形 $A B C D$ 是菱形.

查看试题解析
23. 如图，6×6网格中每个小正方形的边长都为1， $△ A B C$ 的顶点均在网格的格点上.

(1)、填空： $A B =$ ， $B C =$ ， $A C =$ .

(2)、判断 $△ A B C$ 的形状，并说明理由；

(3)、在图中的格点上是否存在点P，使 $∠ A P C = 90 °$ ，请在图中标出所有满足条件的格点P（点B除外）（用 $P_{1}$ 、 $P_{2}$ ……表示）

查看试题解析
24. 先化简，再求值： $a + \sqrt{1 - 2 a + a^{2}}$ ，其中 $a = 2020$ .如图是小亮和小芳的解答过程.

(1)、的解法是错误的；
错误的原因在于未能正确地运用二次根式的性质：；

(2)、先化简，再求值： $a + 2 \sqrt{a^{2} - 8 a + 16}$ ，其中 $a = - 2021$ .

查看试题解析
25. 如图，已知菱形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 相交于点O，过点C作 $C E / / B D$ ，过点D作 $D E / / A C$ ， $C E$ 与 $D E$ 相交于点E.

(1)、求证： $∠ D E C = 90 °$ ；

(2)、若 $A B = 5$ ， $A C = 6$ ，求四边形 $C O D E$ 的周长.

查看试题解析
26. 已知，如图，O为坐标原点，四边形 $O A B C$ 为矩形， $A (20 ， 0)$ ， $C (0 ， 8)$ ，点D是 $O A$ 的中点，动点P在线段 $C B$ 上以每秒4个单位长度的速度由点C向B运动.设动点P的运动时间为t秒.

(1)、当四边形 $P O D B$ 是平行四边形时，求t的值；

(2)、在直线 $C B$ 上是否存在一点Q，使得O、D、Q、P四点为顶点的四边形是菱形？若存在，求t的值，并求出Q点的坐标；若不存在，说明理由；

(3)、在线段 $P B$ 上有一点M，且 $P M = 10$ ，当四边形 $O A M P$ 的周长最小时，求点P运动时间t的值.

查看试题解析