广西壮族自治区崇左市宁明县2020-2021学年八年级下学期期中数学试卷

试卷更新日期：2022-04-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数中，自变量x的取值范围是x＞3的是（）

A、y＝ $\sqrt{x - 3}$ B、y＝ $\frac{1}{\sqrt{x - 3}}$ C、y＝ $\sqrt{3 - x}$ D、y＝ $\sqrt{x + 3}$

查看试题解析
2. 计算 $\sqrt{(- 5)^{2}}$ 的结果为（）

A、 $\sqrt{5}$ B、±5 C、-5 D、5

查看试题解析
3. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{9}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
4. 下列计算正确的是（）

A、 $2 \sqrt{3} + 3 \sqrt{2} = 5$ B、 $\sqrt{8} \div \sqrt{2} = 2$ C、 $5 \sqrt{3} \times 5 \sqrt{2} = 5 \sqrt{6}$ D、 $\sqrt{4 \frac{1}{2}} = 2 \sqrt{\frac{1}{2}}$

查看试题解析
5. 下列方程中，是一元二次方程的为（）

A、 $x + 2 = 1$ B、 $x + 3 y = 4$ C、 $x^{2} - 5 x = 0$ D、 $x + y = 2$

查看试题解析
6. 若m是一元二次方程 $x^{2} - 4 x - 1 = 0$ 的根，则代数式 $4 m - m^{2}$ 的值为（）

A、1 B、-1 C、2 D、-22

查看试题解析
7. 一元二次方程 $x (x - 2) = 2 - x$ 的根是（）

A、﹣1 B、2 C、1和2 D、﹣1和2

查看试题解析
8. 若关于 $x$ 的一元二次方程 $k^{2} x^{2} - (2 k + 1) x + 1 = 0$ 有两个实数根，则 $k$ 的取值范围是（）

A、 $k > - \frac{1}{4}$ B、 $k \geq - \frac{1}{4}$ C、 $k > - \frac{1}{4}$ 且 $k \neq 0$ D、 $k \geq - \frac{1}{4}$ 且 $k \neq 0$

查看试题解析
9. △ABC的三边的长a、b、c满足： $(a - 1)^{2} + \sqrt{b - 2} + | c - \sqrt{5} | = 0$ ，则△ABC的形状为（）.

A、等腰三角形 B、等边三角形 C、钝角三角形 D、直角三角形

查看试题解析
10. 如图，矩形纸片ABCD中，AB＝8cm，把矩形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，若AF＝ $\frac{25}{4}$ cm，则AD的长为（）

A、4cm B、5cm C、6cm D、7cm

查看试题解析
11. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（）

A、7.5平方千米 B、15平方千米 C、75平方千米 D、750平方千米

查看试题解析
12. 在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm² ，设金色纸边的宽为xcm，那么x满足的方程是（）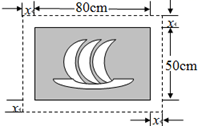

A、x²+65x-350=0 B、x²+130x-1400=0 C、x²-130x-1400=0 D、x²-65x-350=0

查看试题解析

二、填空题

13. 比较大小： $3 \sqrt{2}$ $2 \sqrt{3}$ （填“＞”或“＜”＝）.

查看试题解析
14. 计算 $(\sqrt{3} - 1) (\sqrt{3} + 1)$ 的结果等于．

查看试题解析
15. 已知 $a$ 为实数，且满足 $(a^{2} + b^{2})^{2} + 2 (a^{2} + b^{2}) - 15 = 0$ ，则代数式 $a^{2} + b^{2}$ 的值为.

查看试题解析
16. 一元二次方程 $x^{2} - x - 6 = 0$ 的两根分别是 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2}$ 的值为.

查看试题解析
17. 一直角三角形的边长分别为 $a ， b ， c$ ，若 $a^{2} = 9$ ， $b^{2} = 16$ ，那么 $c$ 的值是.

查看试题解析
18. 如图，长为12cm的弹性皮筋AB直放置在x轴上，固定两端A和B，然后把中点C向上拉升8cm至D点，则弹性皮筋被拉长了；

查看试题解析

三、解答题

19. 计算： $(2 - \sqrt{3})^{2020} (2 + \sqrt{3})^{2021} - 2 \times \sqrt{\frac{3}{4}} - (- 2)^{0}$

查看试题解析
20. 解方程：（x+2）（x-5）=18.

查看试题解析
21. 观察下列等式：
① $\sqrt{2 \times 4 + 1} = 3$ ② $\sqrt{3 \times 5 + 1} = 4$ ③ $\sqrt{4 \times 6 + 1} = 5$ $⋯$

(1)、写出式⑤：；

(2)、试用含n（n为自然数，且 $n \geq 1$ ）的等式表示这一规律，并加以验证.

查看试题解析
22. 网络购物已成为新的消费方式，催生了快递行业的高速发展.某快递公司2020年9月份与11月份投递的快递件数分别为10万件和14.4万件，假定每月投递的快递件数的增长率相同，求该快递公司投递的快递件数的月平均增长率.

查看试题解析
23. 如图，△ABC中，∠C＝90º，AD是角平分线，CD＝15，BD＝25.求AC的长.

查看试题解析
24. 已知关于 $x$ 的一元二次方程 $a x^{2} + b x + \frac{1}{2} = 0$ .

(1)、若 $x = 1$ 是方程的一个解，写出 $a$ ， $b$ 满足的关系式？

(2)、当 $b = 1$ 时，利用根的判别式判断方程根的情况.

(3)、若方程有两个相等的实根，请写出一组满足条件的 $a$ ， $b$ 的值，并求出此时的方程根.

查看试题解析
25. 如图，在平面直角坐标系xOy中，已知点A（﹣1，5），B（1，0），C（3，1），连接BC.

(1)、在图中画出点A关于y轴的对称点 $A^{'}$ ，连接 $A^{'} B ， A^{'} C$ ，并直接写出点 $A^{'}$ 的坐标；

(2)、在（1）的基础上，试判断△ $A^{'} B C$ 的形状，并说明理由.

查看试题解析
26. 如图，在△ABC中，∠ACB=90°，AC=BC，延长AB至点D，使DB=AB，连接CD，以CD为直角边作等腰三角形CDE，其中∠DCE=90°，连接BE.

(1)、求证：△ACD≌△BCE；

(2)、若AC=3cm，则BE= cm.

查看试题解析