广西壮族自治区北海市合浦县2020-2021学年八年级下学期期中数学试卷
试卷更新日期:2022-04-19 类型:期中考试
一、单选题
-
1. 下列图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在▱ABCD中,下列结论一定正确的是( )
2. 在▱ABCD中,下列结论一定正确的是( ) A、AC⊥BD B、∠A+∠B=180° C、AB=AD D、∠A≠∠C3. 下列各组数是勾股数的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列说法正确的是( )A、对角线相等的四边形是平行四边形 B、对角线互相垂直的四边形是正方形 C、矩形的对角线一定互相垂直 D、四条边相等的四边形是菱形5. 如图,在 中, ,直线MN垂直平分AB交AB于M,交BC于N,且 , ,则BN的长为( )
A、AC⊥BD B、∠A+∠B=180° C、AB=AD D、∠A≠∠C3. 下列各组数是勾股数的是( )A、 , , B、 , , C、 , , D、 , ,4. 下列说法正确的是( )A、对角线相等的四边形是平行四边形 B、对角线互相垂直的四边形是正方形 C、矩形的对角线一定互相垂直 D、四条边相等的四边形是菱形5. 如图,在 中, ,直线MN垂直平分AB交AB于M,交BC于N,且 , ,则BN的长为( ) A、4cm B、3.5cm C、3cm D、4.5cm6. 如图,在平行四边形 中, 平分 ,则平行四边形 的周长是( )
A、4cm B、3.5cm C、3cm D、4.5cm6. 如图,在平行四边形 中, 平分 ,则平行四边形 的周长是( ) A、16 B、18 C、20 D、247. 如图,在的正方形网格中, , , , 四条线段的端点都在格点处,则这四条线段长度是无理数的有( )
A、16 B、18 C、20 D、247. 如图,在的正方形网格中, , , , 四条线段的端点都在格点处,则这四条线段长度是无理数的有( ) A、条 B、条 C、条 D、条8. 如图三角形纸片,剪去角后,得到一个四边形,则( )
A、条 B、条 C、条 D、条8. 如图三角形纸片,剪去角后,得到一个四边形,则( ) A、 B、 C、 D、9. 如图,在 中, , ,点 在 上, , ,则 的长为( )
A、 B、 C、 D、9. 如图,在 中, , ,点 在 上, , ,则 的长为( ) A、 B、 C、 D、10. 如图,正方形的对角线与相交于点 , 将绕点顺时针旋转,设旋转角为(),角的两边分别与 , 交于点 , , 连接 , , , 下列四个结论:①;②;③;④;其中正确结论的个数是( )
A、 B、 C、 D、10. 如图,正方形的对角线与相交于点 , 将绕点顺时针旋转,设旋转角为(),角的两边分别与 , 交于点 , , 连接 , , , 下列四个结论:①;②;③;④;其中正确结论的个数是( )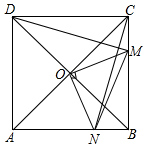 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若中, , , 则.12. 如图,P是 的平分线上一点, 于点A,Q是射线 上一个动点,若 ,则 的最小值为 .
 13. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.
13. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.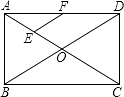 14. 如图,在▱ABCD中,AB=10,AD=6,AC⊥BC.则BD=.
14. 如图,在▱ABCD中,AB=10,AD=6,AC⊥BC.则BD=. 15. 如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2 ,则AB的长为.
15. 如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2 ,则AB的长为.
三、解答题
-
16. 如图,中, , , 为延长线上一点,点在上,且.求证:.
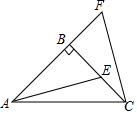 17. 如图,在中, , 分别是 , 上的点,且.求证:四边形是平行四边形.
17. 如图,在中, , 分别是 , 上的点,且.求证:四边形是平行四边形. 18. 如图,平分 , 点 , 分别在 , 上,点在上,且.求证:.
18. 如图,平分 , 点 , 分别在 , 上,点在上,且.求证:. 19. 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A′处,问梯子底部B将外移多少米?
19. 如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时梯子底部B到墙底端的距离为0.7米,考虑爬梯子的稳定性,现要将梯子顶部A沿墙下移0.4米到A′处,问梯子底部B将外移多少米? 20. 如图,为中边延长线上的一点,且 , 连接交于点 , 对角线 , 交于点 , 连接.求证:是的中位线.
20. 如图,为中边延长线上的一点,且 , 连接交于点 , 对角线 , 交于点 , 连接.求证:是的中位线.



