2022年北师大版初中数学七年级下学期期中模拟试题2
试卷更新日期:2022-04-19 类型:期中考试
一、单选题
-
1. 如图, , , ACEF,则的度数为( )
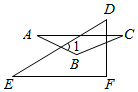 A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,直线 , 与直线 , 相交,已知 , ,则 的度数是( )
A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,直线 , 与直线 , 相交,已知 , ,则 的度数是( )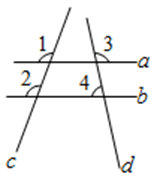 A、 B、 C、 D、4. 若 , , ,则a,b,c的大小关系式( )A、 B、 C、 D、5. 在关系式 中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( ).A、①②⑤ B、①②④ C、①③⑤ D、①④⑤6. 如图所示,将如图一所示的大小相同的四个小正方形按图二所示的方式放置在一个边长为a的大正方形中,中间恰好空出两条互相垂直的宽都为b的长方形,根据图二中阴影部分的面积计算方法可以验证的公式为( )
A、 B、 C、 D、4. 若 , , ,则a,b,c的大小关系式( )A、 B、 C、 D、5. 在关系式 中有下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( ).A、①②⑤ B、①②④ C、①③⑤ D、①④⑤6. 如图所示,将如图一所示的大小相同的四个小正方形按图二所示的方式放置在一个边长为a的大正方形中,中间恰好空出两条互相垂直的宽都为b的长方形,根据图二中阴影部分的面积计算方法可以验证的公式为( )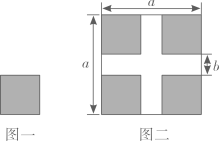 A、(a+b)(a﹣b)=a2﹣b2 B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、(a﹣b)2=(a+b)2﹣4ab7. 如图,直线AB,CD相交于点O,∠AOE=90°,∠DOF=90°,OB平分∠DOG,给出下列结论:
A、(a+b)(a﹣b)=a2﹣b2 B、(a+b)2=a2+2ab+b2 C、(a﹣b)2=a2﹣2ab+b2 D、(a﹣b)2=(a+b)2﹣4ab7. 如图,直线AB,CD相交于点O,∠AOE=90°,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB﹣2∠EOF.其中正确的结论有( )
 A、4个 B、3个 C、2个 D、1个8. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A、4个 B、3个 C、2个 D、1个8. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是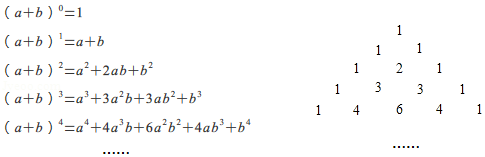 A、2016 B、2017 C、2018 D、2019
A、2016 B、2017 C、2018 D、2019二、填空题
-
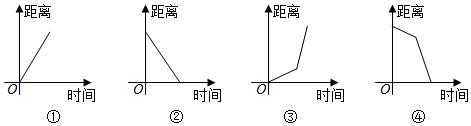
9. 小明早上步行去车站,然后坐车去学校.如图象中,能近似的刻画小明离学校的距离随时间变化关系的图象是 . (填序号)
 10. 如图所示,一个宽度相等的纸条按如图所示方法折叠一下,则∠1= .
10. 如图所示,一个宽度相等的纸条按如图所示方法折叠一下,则∠1= .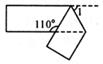 11. 已知a-=3,则a2+的值是.12. 一个长方形,它的面积为6a2﹣9ab+3a,已知这个长方形的长为3a,则宽为 .13. 如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOC=130°,则∠DOE=。
11. 已知a-=3,则a2+的值是.12. 一个长方形,它的面积为6a2﹣9ab+3a,已知这个长方形的长为3a,则宽为 .13. 如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOC=130°,则∠DOE=。 14. 已知a1= ,a2= ,a3= ,…,an= ,Sn=a1•a2…an , 则S2015=.15. 现有A、B、C三种型号的地板砖,其规格如图所示,若用这三种地板砖铺设一个长为 ,宽为 的长方形地面,则需要B种地砖块.
14. 已知a1= ,a2= ,a3= ,…,an= ,Sn=a1•a2…an , 则S2015=.15. 现有A、B、C三种型号的地板砖,其规格如图所示,若用这三种地板砖铺设一个长为 ,宽为 的长方形地面,则需要B种地砖块.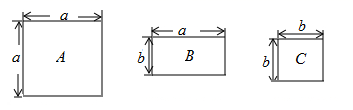 16. 如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为.
16. 如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为.
三、解答题
-
17. 某天数学课上,小明学习了整式的除法运算,放学后,小明回到家拿出课堂笔记,认真地复习课上学习的内容.他突然发现一道三项式除法运算题:(21x4y3-
 +7x2y2)÷(-7x2y)=
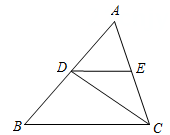
+7x2y2)÷(-7x2y)= +5xy-y,被除式的第二项被墨水弄污了,商的第一项也被墨水弄污了,你能算出两处被污染的内容是什么吗? 18. 已知,如图,CD平分∠ACB, ,∠AED=82°.求∠EDC的度数.下面是小明同学的证明过程,请在括号内填上恰当的依据.
+5xy-y,被除式的第二项被墨水弄污了,商的第一项也被墨水弄污了,你能算出两处被污染的内容是什么吗? 18. 已知,如图,CD平分∠ACB, ,∠AED=82°.求∠EDC的度数.下面是小明同学的证明过程,请在括号内填上恰当的依据.
证明: (已知)
∴∠ACB=∠AED( )
∠EDC=∠DCB( )
又∵CD平分∠ACB(已知)
∴ ( )
又∵∠AED=82°(已知)
∴∠ACB=82°( )
∴ ,
∴∠EDC=∠DCB=41°( )
19. 如图,在折线中,已知 , 延长、交于点 , 猜想与的关系,并说明理由.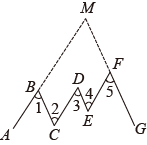 20. 已知A,B,C为△ABC的三边,且a2+b2+b2=ab+bc+ac,试判断△ABC的形状,并说明理由21. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
20. 已知A,B,C为△ABC的三边,且a2+b2+b2=ab+bc+ac,试判断△ABC的形状,并说明理由21. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.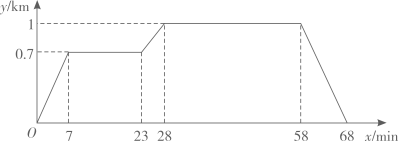
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍 ,图书馆离宿舍 .周末,小亮从宿舍出发,匀速走了 到食堂;在食堂停留 吃早餐后,匀速走了 到图书馆;在图书馆停留 借书后,匀速走了 返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
0.7
(2)、填空:①食堂到图书馆的距离为 .
②小亮从食堂到图书馆的速度为 .
③小亮从图书馆返回宿舍的速度为 .
④当小亮离宿舍的距离为 时,他离开宿舍的时间为 .
(3)、当 时,请直接写出y关于x的函数解析式.四、综合题
-
22. 先化简,再求值.(1)、 ,其中 ;(2)、已知 ,求代数式 的值;(3)、已知 ,求 的值.23. 两个边长分别为a和b的正方形如图1所示,其中未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2..
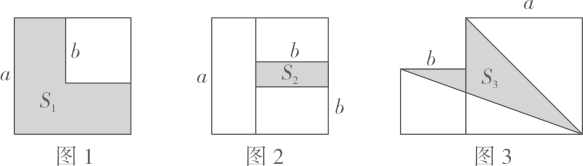 (1)、用含a,b的代数式分别表示S1 , S2;(2)、若a+b=10,ab=22,求S1+S2的值;(3)、当S1+S2=32时,求出图3中阴影部分的面积S3.24. 如图,已知AM∥BN,∠A=52°,点P是射线AM上的动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)、用含a,b的代数式分别表示S1 , S2;(2)、若a+b=10,ab=22,求S1+S2的值;(3)、当S1+S2=32时,求出图3中阴影部分的面积S3.24. 如图,已知AM∥BN,∠A=52°,点P是射线AM上的动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.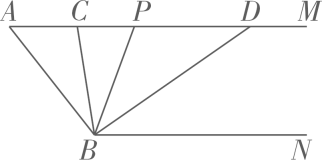 (1)、求∠CBD的度数;(2)、当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
(1)、求∠CBD的度数;(2)、当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由,若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.