北师大版备考2022中考数学二轮复习专题26 统计

试卷更新日期：2022-04-18 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列调查中，适宜采用抽样调查的是（）

A、调查某批次医用口罩的合格率 B、了解某校八年级一班学生的视力情况 C、了解100张百元钞票中有没有假钞 D、调查神舟十四号载人飞船各零部件的质量

查看试题解析

2. 某餐厅共有7名员工，所有员工的工资如下表所示，则众数、中位数分别是（）

人员	经理	厨师	会计	服务员
人数	1	2	1	3
工资数	8000	5600	2600	1000

A、1000，5600 B、1000，2600 C、2600，1000 D、5600，1000

查看试题解析

3. 如表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：

	甲	乙	丙	丁
平均数（环）	9.8	9.8	9.8	9.8
方差	0.85	0.72	0.88	0.76

根据表中数据，要从中选择一名成绩发挥稳定的运动员参加比赛，应选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

4. 在某校选拔毕业晚会主持人的决赛中，参与投票的每名学生必须从进入决赛的四名选手中选1名，且只能选1名，根据投票结果，绘制了如下两幅不完整的统计图，则选手B的得票为（）

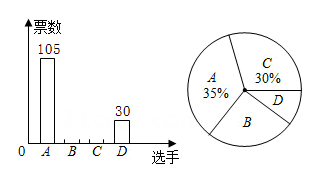A、300 B、90 C、75 D、85

查看试题解析
5. 在某次信息技术能力测试中，人工智能社团的8名同学的成绩统计如图所示，由统计图可知这组数据的中位数是（）

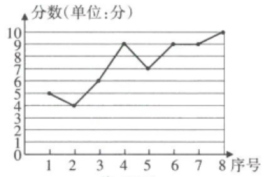A、6分 B、7分 C、8分 D、9分

查看试题解析
6. 现有12块完全相同的巧克力，每块至多被分为两小块，如果这12块巧克力可以平均分给n名同学，则n不可以为（）

A、20 B、18 C、15 D、14

查看试题解析
7. 若一组数据 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 的平均数为4，方差为3，那么数据 $a_{1} + 2$ ， $a_{2} + 2$ ， $a_{3} + 2$ 的平均数和方差分别是（）

A、4， 3 B、6 $，$ 3 C、3 $，$ 4 D、6 5

查看试题解析
8. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ =（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析
9. 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是（）

A、平均数为10，方差为2 B、平均数为11，方差为3 C、平均数为11，方差为2 D、平均数为12，方差为4

查看试题解析
10. 根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
11.
为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：m³），绘制了统计图．如图所示，下面四个推断（　　）
①年用水量不超过180m³的该市居民家庭按第一档水价交费；
②年用水量超过240m³的该市居民家庭按第三档水价交费；
③该市居民家庭年用水量的中位数在150﹣180之间；
④该市居民家庭年用水量的平均数不超过180．

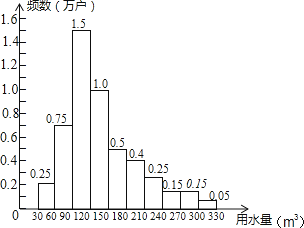A、①③ B、①④ C、②③ D、②④

查看试题解析
12. 今年的“六•一”儿童节是个星期五，某校学生会在初一年级进行了学生对学校作息安排的三种期望（全天休息、半天休息、全天上课）的抽样调查，并把调查结果绘成了下面两个统计图，已知此次被调查的男、女学生人数相同．根据图中信息，下列判断：①在被调查的学生中，期望全天休息的人数占53%；②本次调查了200名学生；③在被调查的学生中，有30%的女生期望休息半天；④若该校现有初一学生900人，根据调查结果估计期望至少休息半天的学生超过了720人．其中正确的判断有（）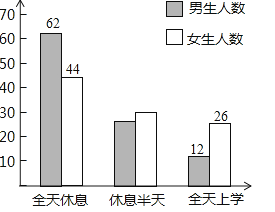

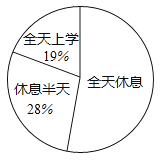A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

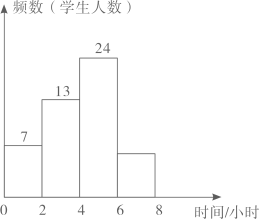
13. 为了解某学校“书香校园”的建设情况，这个学校共有300名学生，检查组在该校随机抽取50名学生，调查了解他们一周阅读课外书籍的时间，并将调查结果绘制成如图所示的频数直方图（每小组的时间值包含最小值，不包含最大值），若要根据图中信息绘制每组人数的扇形统计图，一周课外阅读时间不少于6小时的这部分扇形的圆心角是°.

查看试题解析
14. 小明某学期数学平时成绩为90分，期中考试成绩为80分，期末成绩为90分，计算学期总评成绩的方法：平时占20%，期中占30%，期末占50%，则小明这学期的总评成绩是分．

查看试题解析
15. 为迎接体育测试，小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

其中有三天的个数被墨汁覆盖了，但小强已经计算出这组数据唯一的众数是13，平均数是12，那么这组数据的方差是。

查看试题解析
16. 某学校九（1）班40名同学的期中测试成绩分别为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ，……， $a_{40}$ .已知 $a_{1}$ + $a_{2}$ + $a_{3}$ +……+ $a_{40}$ = 4800，y= ${(a - a_{1})}^{2}$ + ${(a - a_{2})}^{2}$ + ${(a - a_{2})}^{2}$ +……+ ${(a - a_{40})}^{2}$ ，当y取最小值时，的值为.

查看试题解析
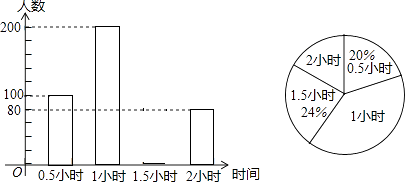
17.
为了解学生参加户外活动的情况，和谐中学对学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：
（Ⅰ）被抽样调查的学生有人，并补全条形统计图；
（Ⅱ）每天户外活动时间的中位数是（小时）；
（Ⅲ）该校共有2000名学生，请估计该校每天户外活动时间超过1小时的学生有人？

查看试题解析
18. 已知数据 $x_{1}$ ， $x_{2}$ ， $\dots$ ， $x_{n}$ 的方差是 $0.1$ ，则 $4 x_{1} - 2$ ， $4 x_{2} - 2$ ， $\dots$ ， $4 x_{n} - 2$ 的方差为.

查看试题解析
19. 已知：一组自然数1，2，3…k，去掉其中一个数后剩下的数的平均数为16，则去掉的数是．

查看试题解析
20. 如果一组按从小到大排序的数据a，b，c的平均数是b，方差是S² ，那么数据a+99，b+100，c+101的方差将 S²（填“大于”“小于”或“等于”）.

查看试题解析

三、计算题

21. 已知两个有理数：－9和5．

(1)、计算： $\frac{(- 9) + 5}{2}$ ；

(2)、若再添一个负整数 $m$ ，且－9，5与 $m$ 这三个数的平均数仍小于m，求m的值．

查看试题解析

四、解答题

22. 某校九年级（1）班的一个数学学习小组对全班某次测试中的“一道满分值为6分的解答题得分”情况进行了统计，绘制成下列不完整的统计图（学生得分均为整数）：

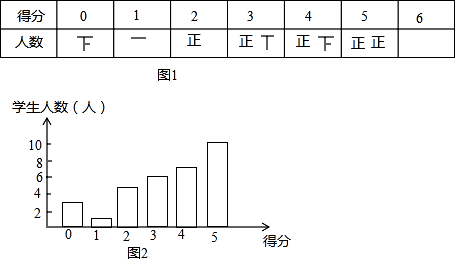
已知全班同学此题的平均得分为4分，结合表格解决下列问题：

(1)、完成表格，并求该班学生总数；

(2)、根据表中提供的数据，补全条形统计图；并判断下列说法中正确的有．（填序号即可）
①该班此题得分的众数是6；

②“随机抽取该班一份试卷，此题得1分”是不可能事件；

③该班学生此题得分的中位数是4；

④若将“该班同学本道题的得分情况”绘制成扇形统计图，求“此题得0分”的人数所对应的圆心角的度数为36°；

(3)、若本年级学生共有540人，请你估计整个年级中此题得满分的学生人数．

查看试题解析
23. 某校九年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如下表，并绘制了如图所示的两幅不完整的统计图，已知B、E两组发言人数的比为5：2，请结合图中相关数据回答下列问题：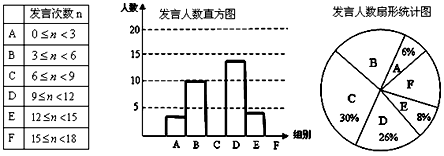

(1)、样本容量是，并补全直方图；

(2)、该年级共有学生800人，请估计该年级在这天里发言次数不少于12次的人数；

(3)、已知A组发言的学生中恰有1位女生，E组发言的学生中有2位男生，现从A组与E组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好都是男生的概率.

查看试题解析

五、综合题

24. 为了防控新冠疫情，某地区积极推广疫苗接种工作，卫生防疫部门对该地区八周以来的相关数据进行收集整理，绘制得到如下图表：

该地区每周接种疫苗人数统计表

周次

第1周

第2周

第3周

第4周

第5周

第6周

第7周

第8周

接种人数（万人）

该地区全民接种疫苗情况扇形统计图

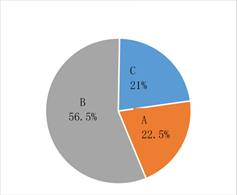
A：建议接种疫苗已接种人群

B：建议接种疫苗尚未接种人群

C：暂不建议接种疫苗人群

根据统计表中的数据，建立以周次为横坐标，接种人数为纵坐标的平面直角坐标系，并根据以上统计表中的数据描出对应的点，发现从第3周开始这些点大致分布在一条直线附近，现过其中两点 $(3 ， 12)$ 、 $(8 ， 42)$ 作一条直线（如图所示，该直线的函数表达式为 $y = 6 x - 6$ ），那么这条直线可近似反映该地区接种人数的变化趋势.

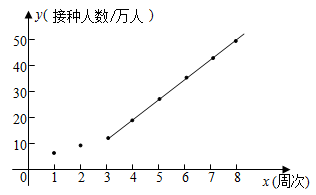
请根据以上信息，解答下列问题：

(1)、这八周中每周接种人数的平均数为万人：该地区的总人口约为万人；

(2)、若从第9周开始，每周的接种人数仍符合上述变化趋势.

①估计第9周的接种人数约为 ▲ 万人；

②专家表示：疫苗接种率至少达60%，才能实现全民免疫.那么，从推广疫苗接种工作开始，最早到第几周，该地区可达到实现全民免疫的标准？

(3)、实际上，受疫苗供应等客观因素，从第9周开始接种人数将会逐周减少

a (a > 0)

万人，为了尽快提高接种率，一旦周接种人数低于20万人时，卫生防疫部门将会采取措施，使得之后每周的接种能力一直维持在20万人.如果

a = 1.8

，那么该地区的建议接种人群最早将于第几周全部完成接种？

查看试题解析

25. 为提高节水意识，小申随机统计了自己家7天的用水量，并分析了第3天的用水情况，将得到的数据进行整理后，绘制成如图所示的统计图.（单位：升）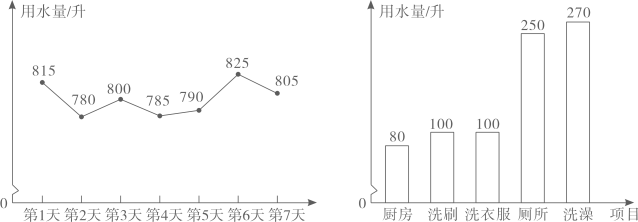

(1)、求这7天内小申家每天用水量的平均数和中位数；

(2)、求第3天小申家洗衣服的水占这一天总用水量的百分比；

(3)、请你根据统计图中的信息，给小申家提出一条合理的节约用水建议，并估算采用你的建议后小申家一个月（按30天计算）节约的用水量。

查看试题解析

数据	37	38	39	40	41
频数	8	4	5	a	1