2022年江苏省无锡市中考数学模拟卷1

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. a（ $a \neq 0$ ）的相反数是（）

A、 $- a$ B、 $a^{2}$ C、 $| a |$ D、 $\frac{1}{a}$

查看试题解析
2. 在下列等式中，不满足a≠0这个条件的是（　　）

A、a⁰＝1 B、 $a^{- 1} = \frac{1}{a}$ C、 $\sqrt{{(\frac{1}{a})}^{2}} = \frac{1}{a}$ D、 ${(\sqrt{a})}^{2} = a^{4}$

查看试题解析
3. 对于数据：6，3，4，7，6，0，9．下列判断中正确的是（）

A、这组数据的平均数是6，中位数是6 B、这组数据的平均数是6，中位数是7 C、这组数据的平均数是5，中位数是6 D、这组数据的平均数是5，中位数是7

查看试题解析
4. 方程组 ${\begin{array}{l} x + y = 2 \\ 3 x + y = 4 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 0 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = - 3 \end{array}$

查看试题解析
5. 下列运算正确的是（）

A、(-2a²b)³＝-6a⁶b³ B、a⁴·a²＝a⁸ C、a⁶÷a³＝a² D、(-a²)³＝-a⁶

查看试题解析
6. 中国传统纹饰图案不但蕴含了丰富的文化，而且大多数图案还具有对称美．下列纹饰图案中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，在平行四边形ABCD中，E为CD上一点，DE：CE＝3：4，连接AE交对角线BD于点F，则S_△_DEF：S_△_ADF：S_△_ABF等于（）

A、3：4：7 B、9：16：49 C、9：21：49 D、3：7：49

查看试题解析
8. 如图，直线y=x+2与反比例函 $y = \frac{k}{x}$ 的图象在第一象限交于点P.若 $O P = \sqrt{20}$ ，则k的值为（）

A、6 B、8 C、10 D、12

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = \sqrt{5}$ .以 $A B$ 为直径作 $⊙ O$ ，作直径 $C D$ ，连结 $A D$ 并延长至点E，使 $D E = A D$ ，连结 $C E$ 交 $A B$ 于点F， $D G / / A B$ 交 $C E$ 于点G.若 $A C = 2 E G$ ，则直径 $A B$ 的长为（）

A、 $3 \sqrt{2}$ B、 $\sqrt{19}$ C、 $2 \sqrt{5}$ D、 $\sqrt{21}$

查看试题解析
10. 如图，已知抛物线y=x²-2x与直线y=-x+2交于A，B两点．点M是直线AB上的一个动点，将点M向左平移4个单位长度得到点N，若线段MN与抛物线只有一个公共点，则点M的横坐标x_M的取值范围是（）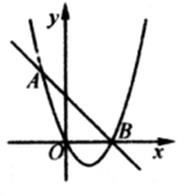

A、-2≤x_M≤2 B、-2≤x_M≤2且x_M≤-1 C、-1≤x_M<2 D、-1≤x_M<2或x_M=3

查看试题解析

二、填空题（每题2分，共16分）

11. 把多项式3m²﹣3分解因式的结果为．

查看试题解析
12. 2022年2月4日，第24届冬奥会在北京开幕，中国大陆地区观看开幕式的人数约316000000人，请把316000000用科学记数法表示出来．

查看试题解析
13. 圆锥的侧面展开图的面积是15πcm² ，母线长为5cm，则圆锥的底面半径长为cm．

查看试题解析
14. 若点 $A (2 ， y_{1})$ 、 $B (3 ， y_{2})$ 都在反比例函数 $y = \frac{5}{x}$ 的图象上，则 $y_{1}$ $y_{2}$ （填“<”、“>”或“=”）．

查看试题解析
15. 如图，某山的斜坡AB的长为300米，坡角∠BAC＝37°，则该斜坡的高BC的长为米（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）.

查看试题解析
16. 下列各组的两个图形：①两个等腰三角形；②两个矩形；③两个等边三角形；④两个正方形；⑤各有一个内角是45°的两个等腰三角形．其中一定相似的是（只填序号）

查看试题解析
17. 如图，已知正方形ABCD，延长AB至点E使BE＝AB，连接CE、DE，DE与BC交于点N，取CE的中点F，连接BF，AF，AF交BC于点M，交DE于点O，则下列结论：①DN＝EN；②OA＝OE；③tan∠CED $= \frac{1}{3}$ ；④S_{四边形BEFM}＝2S_△_CMF ．其中正确的是.（只填序号）

查看试题解析
18. 一个横断面是抛物线的渡槽如图所示，根据图中所给的数据求出水面的宽度是cm．

查看试题解析

三、解答题（共10题，共84分）

19. 计算：

(1)、 ${(m - n)}^{2} - m (m - 2 n)$

(2)、 $\frac{x^{2} - 2 x}{x^{2} - 1} \div (1 - \frac{2 x - 1}{x + 1})$

查看试题解析
20.

(1)、计算： $\sin 60 ° - \sqrt{12} \times \sqrt{3} - {(π - 3.14)}^{0} + 2^{- 2}$

(2)、解不等式组 ${\begin{matrix} 2 x + 7 \geq 1 - x ， ① \\ 6 - 3 (1 - x) > 5 x ， ② \end{matrix}$

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $∠ B A D = ∠ B C D$ ，点 $E$ 在 $B D$ 的延长线上，点 $F$ 在 $D B$ 的延长线上，且 $D E = B F$ ，连接 $A E$ ， $C F$ ．求证：

(1)、 $A D = C B$ ；

(2)、 $A E ∥ C F$ ．

查看试题解析
22. 在一个不透明的袋子中，放有四张质地完全相同的卡片，分别标有数字“ $- 3 ， - 2 ， 1 ， 6$ ”．

(1)、随机抽出一张卡片是负数的概率是；

(2)、第一次从袋中随机地抽出一张卡片，把所抽到的数字记为横坐标 $m$ ，不放回袋中，再随机地从中抽出一张，把所抽到的数字记为纵坐标 $n$ ．请用数状图或列表法求所得的点 $(m ， n)$ 在反比例函数 $y = \frac{6}{x}$ 上的概率．

查看试题解析
23. 疫情防控已成为常态化，为了解学生对疫情防控措施的知晓情况，某校保健室开展了“疫情防控知识”问卷测试（满分10分）．他们将全校学生成绒进行统计，并随机抽取了40位同学的成绩绘制成如下的频数分布表和频数分布直方图（不完整）．
组号
成绩
频数
频率
1
$4 \leq x < 5$
2
0.050
2
$5 \leq x < 6$
6
0.150
3
$6 \leq x < 7$
a
0.450
4
$7 \leq x < 8$
9
0.225
5
$8 \leq x < 9$
b
m
6
$9 \leq x < 10$
2
0.050

合计
40
1.000
根据以上提供的信息，解答下列问题：

(1)、表格中 $a =$ ， $b =$ ， $m =$ ；补全频数分布直方图；

(2)、这40位同学成绩的中位数落在哪一个小组？

(3)、全校共有1200位同学参与测试，若以组中值（每组成绩的中间数值）为本组数据的代表，请估计所有同学成绩的平均分大约是多少？

查看试题解析
24. 如图，已知锐角 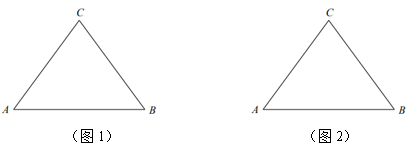$△ A B C$ 中， $A C = B C$ .

(1)、请在图1中用无刻度的直尺和圆规作图：作 $∠ A C B$ 的平分线 $C D$ ；作 $△ A B C$ 的外接圆 $⊙ O$ ；（不写作法，保留作图痕迹）

(2)、在（1）的条件下，若 $A B = \frac{48}{5}$ ， $⊙ O$ 的半径为5，则 $\sin B =$ .（如需画草图，请使用图2）

查看试题解析
25. 如图，AB为⊙O的直径，C为⊙O上一点，经过点C的切线交AB的延长线于点E，AD⊥EC交EC的延长线于点D，连接AC．

(1)、求证：AC平分∠DAE；

(2)、若cos∠DAE $= \frac{2}{3}$ ， BE＝2，求⊙O的半径．

查看试题解析
26. 为加强校园阳光体育活动，某中学计划购进一批篮球和排球，经过调查得知每个篮球的价格比每个排球的价格贵40元，买5个篮球和10个排球共用1100元.

(1)、求每个篮球和排球的价格分别是多少？

(2)、某学校需购进篮球和排球共120个，总费用不超过9000元，但不低于8900元，问有几种购买方案？最低费用是多少？

查看试题解析
27. 已知抛物线y=ax²+bx+c（a≠0）的顶点在×轴上．

(1)、若抛物线过点P（0， $\frac{1}{4}$ ），求证：a=b²？；

(2)、已知点P₁（-2，1），P₂（2，-1），P₃（2，1）中恰有两点在抛物线上
①求抛物线的解析式；

②设直线l：y= $\frac{3}{4}$ x+1与抛物线交于A，B两点，点M在直线y=n（n<0）上，过A，B两点分别作直线y=n（n<0）的垂线，垂足为C，D．是否存在这样的n的值，使得以点A，C，M为顶点的三角形与△BDM相似的点M恰有两个？若存在，请直接写出n的值；若不存在，请说明理由．

查看试题解析
28. 已知，如图1，Rt△ABC中，AB＝AC，∠BAC＝90°，D为△ABC外一点，且∠ADC＝90°，E为BC中点，AF∥BC，连接EF交AD于点G，且EF⊥ED交AC于点H，AF＝1．

(1)、若 $\frac{A H}{C H} = \frac{1}{3}$ ，求EF的长；

(2)、在（1）的条件下，求CD的值；

(3)、如图2，连接BD，BG，若BD＝AC，求证：BG⊥AD．

查看试题解析

组号	成绩	频数	频率
1	$4 \leq x < 5$	2	0.050
2	$5 \leq x < 6$	6	0.150
3	$6 \leq x < 7$	a	0.450
4	$7 \leq x < 8$	9	0.225
5	$8 \leq x < 9$	b	m
6	$9 \leq x < 10$	2	0.050
	合计	40	1.000