2022年江苏省盐城市中考数学模拟卷1

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共24分）

1. ﹣ $\frac{1}{2120}$ 的绝对值是（）

A、﹣2020 B、﹣ $\frac{1}{2120}$ C、 $\frac{1}{2120}$ D、2020

查看试题解析
2. 计算（-x²） ·（-x³）⁴的结果为（）

A、-x⁹ B、x⁹ C、-x¹⁴ D、x¹⁴

查看试题解析
3. 下列冬奥会会徽图案中，既是轴对称图形、又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 由四个完全相同的正方体组成的几何体如图所示，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
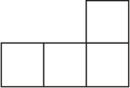5. 2022年1月15日，国家卫健委新闻发言人在国务院联防联控机制新闻发布会上表示，要持续推进新冠病毒疫苗接种，截止14日，完成全程接种的人数为122058.4万人，其中数据122058.4万用科学记数法表示为（）

A、 $1.220584 \times 1 0^{5}$ B、 $1.2 \times 1 0^{9}$ C、 $1.220584 \times 1 0^{9}$ D、 $1.220584 \times 1 0^{13}$

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ A = 30 °$ ，点 $D$ 是 $A B$ 延长线上一点，过点 $D$ 作 $E F ∥ B C$ ．若 $∠ A D E = 70 °$ ，则 $∠ C$ 的度数为（）

A、20° B、30° C、40° D、50°

查看试题解析
7. 若 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 5 x + 6 = 0$ 的两个根，则 $x_{1} + x_{2}$ ， $x_{1} x_{2}$ 的值分别是（）

A、1和6 B、5和-6 C、-5和6 D、5和6

查看试题解析
8. 如图，已知△ABC 中，∠C＝90°，AC＝BC＝ $\sqrt{2}$ ，将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置，连接 C′B，则 C′B 的长为（）

A、2－ $\sqrt{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\sqrt{3} - 1$ D、1

查看试题解析

二、填空题（每题3分，共24分）

9. 七名学生投篮球，每人投了10个球后，统计他们每人投中球的个数．得到七个数据，并对数据进行整理和分析，得出如下信息：

平均数

中位数

众数

最小值

$m$

6

7

2

已知小宇投中了4个，下列判断

①可能有学生投中了9个 ②投中6个的学生只有1人

③这七个数据之和可能为42 ④ $m$ 的值可能为5

所有正确推断的序号是．

查看试题解析
10. 分解因式 $1 + m + \frac{m^{2}}{4} =$ ．

查看试题解析
11. 若一个多边形的一条对角线把它分成两个四边形，则这个多边形的内角和是度.

查看试题解析
12. 圆内接四边形ABCD中，已知∠A=70°，则∠C=

查看试题解析
13. 如图，在Rt△ABC中，∠ACB=90°，D，E，F分别是AB，AC，AD的中点，若EF=3，则AB的长为.

查看试题解析
14. 已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是.

查看试题解析
15. 为了响应全民阅读的号召，某校图书馆利用节假日面向社会开放．据统计，第一个月进馆560人次，进馆人次逐月增加，第三个月进馆830人次．设该校图书馆第二个月、第三个月进馆人次的平均增长率为x，则可列方程为．

查看试题解析
16. 如图，在等腰 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = B C = 4 \sqrt{2}$ .点 $D$ 和点 $E$ 分别在 $B C$ 边和 $A B$ 边上，连接 $D E$ .将 $△ B D E$ 沿 $D E$ 折叠，得到 $△ B^{^{'}} D E$ ，点 $B$ 恰好落在 $A C$ 的中点处.设 $D E$ 与 $B B^{'}$ 交于点 $F$ ，则 $D E =$ .

查看试题解析

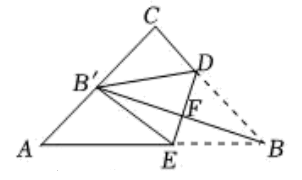
三、解答题（共11题，共102分）

17. 计算：2^﹣1+4cos45° $- \sqrt{8} +$ （π﹣2022）⁰ ．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 4 x - 5 > 3 (x - 2) \\ \frac{x + 10}{3} > 2 x \end{array}$

查看试题解析
19. 先化简，再求值：（1 $- \frac{5}{x ＋ 2} ） \div \frac{x^{2} - 6 x ＋ 9}{x ＋ 2}$ ，其中x＝3 $- \sqrt{3}$ .

查看试题解析
20. 已知二次函数y=a（x-1）²+k的图象与y轴交于点C（0，-8），与x轴的一个交点坐标是A（-2，0）．

(1)、求二次函数的解析式；

(2)、当x为何值时，y<0．

查看试题解析
21. 如图，在6×6的方格纸中，A，B，C均为格点，按要求画图：①仅用无刻度直尺，且不能用直尺的直角；②保留必要的画图痕迹；③标注相关字母。

①作CD⊥AB，使得D为格点．
②在AB上取一点E，使得∠AEC=45°。

查看试题解析
22. 2022年冬奥会将在我国北京和张家口举行，如图所示为冬奥会和冬残奥会的会徽“冬梦”“飞跃”，吉样物“冰墩墩”“雪容融”，将四张正面分别印有以上个图案的卡片（卡片的形状、大小、质地都相同）背面朝上洗匀．

(1)、若从中任意抽取1张，抽得卡片上的图案恰好为“冰墩墩”的概率是．

(2)、若从中任意抽取两张，请用列表或画树状图法求两张卡片上的图案都是会徽的概率．

查看试题解析
23. 如图，AC为矩形ABCD的对角线，AC的垂直平分线交AD、BC于点F、E．

(1)、如图1，求证：四边形AECF为菱形．

(2)、如图2，若 $B C = 5$ ， $A B = \sqrt{5}$ ，请直接写出图中所有正切值等于 $\frac{\sqrt{5}}{2}$ 的角．

查看试题解析
24. 如图，AB是⊙O的直径，点D，E在⊙O上，∠B＝2∠ADE，点C在BA的延长线上.

(1)、若∠C＝∠DAB，求证：CE是⊙O的切线；

(2)、若OF＝2，AF＝3，求EF的长.

查看试题解析
25. 如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37°角的楼梯AD、 BE和一段水平平台DE构成．已知天桥高度BC≈4.8米，引桥水平跨度AC=8米．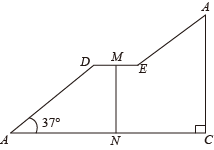
（参考：sin37°=0.60，cos37°=0.80，tan37°=0.75）

(1)、求水平平台DE的长度；

(2)、若与地面垂直的平台立枉MN的高度为3米，求两段楼梯AD与BE的长度之比．

查看试题解析
26. 一队学生从学校出发去劳动基地，行进的路程与时间的函数图象如图所示，队伍走了0.8小时后，队伍中的通讯员按原路加快速度返回学校取材料．通讯员经过一段时间回到学校，取到材料后立即按返校时加快的速度追赶队伍，并比学生队伍早18分钟到达基地．如图，线段OD表示学生队伍距学校的路程y（千米）与时间x（小时）之间的函数关系，折线OABC表示通讯员距学校的路程y（千米）与时间x（小时）之间的函数关系，请你根据图象信息，解答下列问题：

(1)、图中的 $m =$ 千米， $a =$ 小时，点B的坐标为；

(2)、求通讯员距学校的路程y（千米）与时间x（小时）之间的函数关系式；

(3)、若通讯员与学生队伍的距离不超过3千米时能用无线对讲机保持联系，请你直接写出通讯员离开队伍后他们能用对讲机保持联系的时间的取值范围．
答：．

查看试题解析
27. 如图，已知抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于点 $A (1 ， 0)$ 和点 $B (3 ， 0)$ ，与 $y$ 轴交于点 $C$ ．连接 $A C$ ， $B C$ ．

(1)、求抛物线的表达式，并直接写出 $B C$ 所在直线的表达式．

(2)、点 $P$ 为第四象限内抛物线上一点，连接 $A P$ ， $B P$ ，求四边形 $A P B C$ 面积的最大值及此时点 $P$ 的坐标．

(3)、设点 $D$ 是 $B C$ 所在直线上一点，且点 $D$ 的横坐标为 $m$ ．是否存在点 $D$ ，使 $△ A C D$ 为等腰三角形？若存在，直接写出 $m$ 的值；若不存在，请说明理由．

查看试题解析

平均数	中位数	众数	最小值
$m$	6	7	2