2022年江苏省南通市中考数学模拟卷1

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知点A（1，a）、点B（b，2）关于原点对称，则a+b的值为（）

A、3 B、-3 C、-1 D、1

查看试题解析
2. 通过严格实施低碳管理等措施，2022年北京冬奥会和冬残奥会全面实现了碳中和．根据测算，北京冬奥会三个赛区的场馆使用绿电4亿千瓦时，可以减少燃烧12.8万吨标准煤，减少排放二氧化碳32万吨，实现了“山林场馆、生态冬奥”的目标，其中的32万用科学记数法表示为（）

A、 $32 \times 1 0^{4}$ B、 $3.2 \times 1 0^{4}$ C、 $3.2 \times 1 0^{5}$ D、 $3.2 \times 1 0^{6}$

查看试题解析
3. 下列运算正确的是（）

A、(-2a²b)³＝-6a⁶b³ B、a⁴·a²＝a⁸ C、a⁶÷a³＝a² D、(-a²)³＝-a⁶

查看试题解析
4. 下列调查中，适宜采用抽样调查的是（）

A、调查某批次医用口罩的合格率 B、了解某校八年级一班学生的视力情况 C、了解100张百元钞票中有没有假钞 D、调查神舟十四号载人飞船各零部件的质量

查看试题解析
5. 如图是一个几何体的三种视图，则该几何体可能是（）

A、 B、 C、 D、

查看试题解析
6. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，过点 $D$ 作 $D H ⊥ A B$ 于点 $H$ ，连接 $O H$ ，若 $O A = 3$ ， $O H = 2$ ，则菱形 $A B C D$ 的面积为（）

A、 $12$ B、 $18$ C、 $6$ D、 $24$

查看试题解析
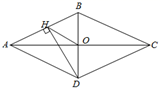7. 《九章算术》中记载：“今有黄金九枚，白银一十一枚，称之适等.交易其一，金轻十三两.问：金、银各一枚各重几何？”译文：“9枚黄金和11枚白银的重量恰好相等，若把一枚黄金和一枚白银交换位置，则原来放黄金那边的重量就要轻13两.问：每枚黄金、白银的重量各多少两？”设每枚黄金 $x$ 两，每枚白银 $y$ 两，则可列方程组为（）

A、 ${\begin{array}{l} 9 x = 11 y \\ (9 - 1) x + y + 13 = (11 - 1) y + x \end{array}$ B、 ${\begin{array}{l} 9 x = 11 y \\ (9 - 1) x + y = (11 - 1) y + x + 13 \end{array}$ C、 ${\begin{array}{l} 11 x = 9 y \\ (9 - 1) x + y + 13 = (11 - 1) y + x \end{array}$ D、 ${\begin{array}{l} 11 x = 9 y \\ (9 - 1) x + y = (11 - 1) y + x + 13 \end{array}$

查看试题解析
8. 若实数 $a$ 既使得关于 $x$ 的不等式组 ${\begin{matrix} \frac{x}{2} + 1 \leq \frac{x + 4}{3} \\ x + 1 > \frac{a + x}{2} \end{matrix}$ 有解，又使得关于 $y$ 的分式方程 $\frac{3 - a y}{3 - y} - 1 = \frac{3}{y - 3}$ 有整数解，则满足条件的所有整数 $a$ 的和为（）

A、4 B、2 C、0 D、-2

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = B C$ ， E是AB的中点，过点E作AC和BC的垂线，垂足分别为点E和点F，四边形CDEF沿着CA方向匀速运动，当点C与点A重合时停止运动，设运动时间为t，运动过程中四边形CDEF与 $△ A B C$ 重叠部分面积为S，则下列图象能大致反应S与t之间函数关系的是（）

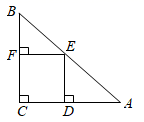A、 B、 C、 D、

查看试题解析
10. 如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B（0，3），抛物线y=﹣x²+2x+1与y轴交于点C，点E在抛物线y=﹣x²+2x+1的对称轴上移动，点F在直线AB上移动，CE+EF的最小值是（）

A、1.4 B、2.5 C、2.8 D、3

查看试题解析

二、填空题（11-12题每题3分，13-18题每题4分，共30分）

11. 计算： $(x - 2 y + 3) (x + 2 y - 3)$ ．

查看试题解析
12. 若一个正多边形的一个外角等于36°，则这个正多边形的边数是.

查看试题解析
13. 已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是.

查看试题解析
14. 小明家、文具店、学校在一条直线上，小明家到学校的路程为 $1000 m$ ．一天，小明在上学途中到文具店买了学习用品，然后以原速的 $1.5$ 倍继续匀速步行到学校，图中的折线反映了这天小明从家步行到学校所走的路程 $s (m)$ 与时间 $t (\min)$ 之间的函数关系，这天小明上学途中共用的时间是 $\min$

查看试题解析
15. 如图，轮船在A处观测灯塔C位于北偏西70°方向上，轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行，2小时后到达码头B处，此时，观测灯塔C位于北偏西25°方向上，则灯塔C与码头B的距离是海里.（结果保留根号）

查看试题解析
16. 设a、b是方程 $x^{2} + x - 2022 = 0$ 的两个实数根，则 ${(a + 1)}^{2} + b$ 的值为.

查看试题解析
17. 当 $2 \leq x \leq 4$ 时，二次函数 $y = - x^{2} + 2 m x$ 的函数值y随自变量x的增大而减小，则m的取值范围是．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，以点A为圆心， $A B$ 长为半径画弧，交 $A C$ 延长线于点D，过点C作 $C E / / A B$ ，交 $\overset{⌢}{B D}$ 于点 $E$ ，连接BE，则 $\frac{C E}{B E}$ 的值为.

查看试题解析

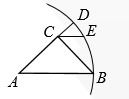
三、解答题（共8题，共90分）

19. 计算：

(1)、 ${(m - n)}^{2} - m (m - 2 n)$

(2)、 $\frac{x^{2} - 2 x}{x^{2} - 1} \div (1 - \frac{2 x - 1}{x + 1})$

查看试题解析
20. 某校初三年级在一次研学活动中，数学研学小组为了估计澧水河某段水域的宽度，在河的对岸选定一个目标点A，在近岸分别取点B、D、E、C ，使点A、B、D在一条直线上，且AD⊥DE，点A、C、E也在一条直线上，且DE $∥$ BC.经测量BC＝25米，BD＝12米，DE＝35米，求河的宽度AB为多少米？

查看试题解析
21. 疫情防控已成为常态化，为了解学生对疫情防控措施的知晓情况，某校保健室开展了“疫情防控知识”问卷测试（满分10分）．他们将全校学生成绒进行统计，并随机抽取了40位同学的成绩绘制成如下的频数分布表和频数分布直方图（不完整）．
组号
成绩
频数
频率
1
$4 \leq x < 5$
2
0.050
2
$5 \leq x < 6$
6
0.150
3
$6 \leq x < 7$
a
0.450
4
$7 \leq x < 8$
9
0.225
5
$8 \leq x < 9$
b
m
6
$9 \leq x < 10$
2
0.050

合计
40
1.000
根据以上提供的信息，解答下列问题：

(1)、表格中 $a =$ ， $b =$ ， $m =$ ；补全频数分布直方图；

(2)、这40位同学成绩的中位数落在哪一个小组？

(3)、全校共有1200位同学参与测试，若以组中值（每组成绩的中间数值）为本组数据的代表，请估计所有同学成绩的平均分大约是多少？

查看试题解析
22. 父亲节快到了，明明准备为爸爸煮四个大汤圆作早点：一个芝麻馅，一个水果馅，两个花生馅，四个汤圆除内部馅料不同外，其它一切均相同．

(1)、求爸爸吃到一个花生馅汤圆，一个芝麻馅汤圆的概率；

(2)、若给爸爸再增加一个花生馅的汤圆，则爸爸吃到一个花生馅汤圆，一个芝麻馅汤圆的可能性是否会增大？请说明理由．

查看试题解析
23. 如图，四边形ABCD内接于⊙O， BD为直径，AC平分∠BCD，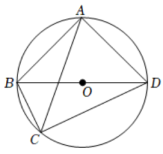

(1)、若BC=5cm，CD=12cm，求AB的长；

(2)、求证：BC+CD= $\sqrt{2}$ AC．

查看试题解析
24. 甲、乙两车匀速从同一地点到距离出发地480千米处的景点，甲车出发半小时后，乙车以每小时80千米的速度沿同一路线行驶，两车分别到达目的地后停止．甲、乙两车之间的距离y（千米）与甲车行驶的时间x（小时）之间的函数关系如图所示．

(1)、甲车行驶的速度是千米/小时．

(2)、求乙车追上甲车后，y与x之间的函数关系式，并写出自变量x的取值范用．

(3)、直接写出两车相距5千米时x的值．

查看试题解析
25. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A B C = 30 °$ ，点D是平面内一动点（不与点C重合），连接CD，将线段CD绕点D顺时针旋转60°，得到线段DE（点E不与点B重合），连接BE．取CD的中点P，连接AP．

(1)、如图（1），当点E落在线段AC上时，
① $\frac{A P}{B E} =$ ；
②直线AP与直线BE相交所成的较小角的度数为．请给予证明．

(2)、如图（2），当点E落在平面内其他位置时，（1）中的两个结论是否仍然成立？若成立，请就图（2）的情形给出证明；若不成立，请说明理由．

(3)、若 $A C = 6$ ， $C P = 3$ ，当点B，D，E在同一条直线上时，请直线写出线段AP的长．

查看试题解析
26. 如图1．抛物线 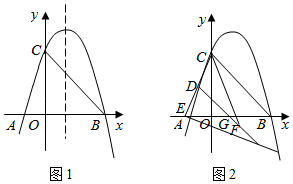$y = - \frac{5}{12} x^{2} + b x + c$ 与 $x$ 轴交于A、 $B$ 两点．交 $y$ 轴于点 $C (0 ， 8)$ ，点 $B (6 ， 0)$ ，连接 $B C$ ．

(1)、求抛物线的解析式；

(2)、 $P (- 4 ， m)$ 为抛物线上一点，点 $Q$ 为 $y$ 轴上一点，点 $M$ 在 $x$ 轴上，求 $P Q + Q M + \frac{4}{5} B M$ 的最小值；

(3)、如图2．点 $D (- 2 ， n)$ 是抛物线上一点， $R$ 为第四象限抛物线上一点，延长 $C D$ 交 $x$ 轴于点 $E$ ，连接 $R E$ ，点 $G (2 ， 0)$ ，直线 $D G$ 与 $R E$ 交于点 $S$ ，点 $F$ 在线段 $D S$ 上，且 $∠ D S E + ∠ B C F = 45 °$ ，已知 $∠ B E S = ∠ F C O$ ，求点 $F$ 的坐标．

查看试题解析

组号	成绩	频数	频率
1	$4 \leq x < 5$	2	0.050
2	$5 \leq x < 6$	6	0.150
3	$6 \leq x < 7$	a	0.450
4	$7 \leq x < 8$	9	0.225
5	$8 \leq x < 9$	b	m
6	$9 \leq x < 10$	2	0.050
	合计	40	1.000