（人教版）2021-2022学年度第二学期八年级数学《特殊的平行四边形》复习卷
试卷更新日期：2022-04-18 类型：复习试卷
一、单选题
-
1. 在数学活动课上，老师和同学们判断一个四边形门框是不是矩形，下面是某合作学习小组的4位同学拟定的方案，其中正确的是（ ）A、测量对角线，看是否互相平分 B、测量两组对边，看是否分别相等 C、测量对角线，看是否相等 D、测量对角线的交点到四个顶点的距离，看是否都相等2. 在 ABCD中，增加一个条件能使它成为矩形，则增加的条件是（ ）A、对角线互相平分 B、AB=BC C、 D、3. 如图，在△ABC中，∠C=90°，∠A=30°，AC的垂直平分线分别交AC.AB于点D，F，过点B作DF的垂线，垂足为E.若BC=2，则四边形BCDE的面积是（ ）
A、 B、 C、4 D、4. 如图所示，D，E，F分别是△ABC三边的中点，添加下列条件后，不能得到四边形DBFE是菱形的是（ ）
A、AB=BC B、BE平分∠ABC C、BE⊥AC D、AB=AC5. 如图所示，若要使平行四边形ABCD成为菱形，则需要添加的条件是（ ）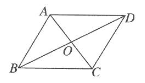
A、AB=CD B、AD=BC C、AB=BC D、AC=BD6. 菱形ABCD的边长AB=5，则此菱形的周长是（ ）A、20 B、25 C、10 D、57. 如图，菱形ABCD中，AE=1，AF=BE=2.若P为对角线BD 上一动点，则EP＋FP的最小值为（ ）
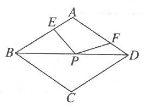A、1 B、2 C、3 D、48. 如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB＝90°，且BC＝2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3 ， 若S1＝4，S3＝12，则S2的值为（ ）
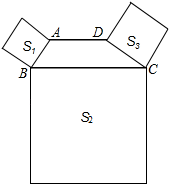A、16 B、24 C、48 D、649. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变.如图，改变正方形ABCD的内角，正方形ABCD变为菱形 ，若 ，则菱形 的面积与正方形ABCD的面积之比是（ ）
A、1 B、 C、 D、10. 在菱形ABCD中，对角线AC与BD相交于点O，添加以下条件，能判定菱形ABCD是正方形的是（ ）
A、AB = AC B、OA = OC C、BC⊥CD D、AC⊥BD二、填空题
-
11. 如图所示，顺次连结四边形ABCD各边中点得四边形GHEF，要使四边形GHEF为矩形，则四边形ABCD 的对角线AC，BD 应满足的条件是.
12. 如图所示，在△ABC中，点D在BC上，过点D分别作AB，AC的平行线，分别交AC，AB于点E，F.如果要得到矩形AEDF，那么△ABC应具备的条件是.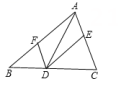
13. 如图，在菱形中，连接 ． 若 ， 则的度数为°．
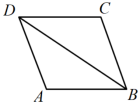14. 如图，O是矩形ABCD对角线的交点，DE// AC，CE//BD，DE和CE相交于点E，已知AB=4，AD=6，则四边形OCED的周长为.
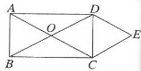15. 建党100周年主题活动中，702班浔浔设计了如图1的“红色徽章”其设计原理是：如图2，在边长为的正方形四周分别放置四个边长为的小正方形，构造了一个大正方形 ， 并画出阴影部分图形，形成了“红色徽章”的图标.现将阴影部分图形面积记作 ， 每一个边长为的小正方形面积记作 ， 若 ， 则的值是.
三、解答题
-
16. 如图，矩形ABCD的对角线AC，BD相交于点O.E，F，G，H分别是OA，OB，OC，OD的中点.求证：四边形 EFGH是矩形.
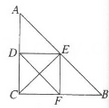
17. 如图所示，在△ABC中，D，E，F分别是AC，AB，BC的中点，且CE= AB.求证：四边形CFED是矩形.
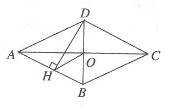
18. 如图所示，四边形ABCD是菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连结OH.求证：∠DHO=∠DCO.
19. 如图，菱形的边长为6， ， 点是上的动点，是上的动点，满足 ， 求证：不论点E、F怎样移动，总是等边三角形．
