（人教版）2021-2022学年度第二学期八年级数学《平行四边形》复习卷
试卷更新日期：2022-04-18 类型：复习试卷
一、单选题
-
1. 在平行四边形中，与的度数之比为 ， 则的度数是（ ）A、 B、 C、 D、2. 已知 ABCD的一边长为5，则对角线AC，BD的长可取下列数据中的（ ）A、2和4 B、3和4 C、4和5 D、5和63. 如图所示，在平行四边形ABCD中，延长边CD到点E，使CE-AD，连结BE交AD于点F，图中等腰三角形有（ ）
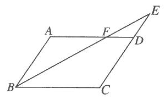A、1个 B、2个 C、3个 D、4个4. 如图，在平行四边形ABCD中，∠ABC的平分线BE交AD于点E，∠AEB=25°，则∠A的大小为（ )
A、100° B、120° C、130° D、150°5. 如图，已知平行四边形ABCD的面积为100，P为边CD上的任意一点，E，F分别是线段PA，PB的中点，则图中阴影部分的总面积为（ ）
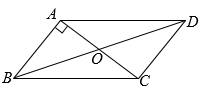
A、30 B、25 C、22.5 D、506. 如图所示，已知四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从C向D移动而点R不动时，那么下列结论成立的是（ ）
A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关7. 如图所示，在四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连结AF，CE，若DE=BF，则下列结论：①CF=AE；②OE=OF；③四边形ABCD是平行四边形；④图中共有四对全等三角形.其中正确结论的个数是（ ）
A、4个 B、3个 C、2个 D、1个8. 如图所示，在△ABC中，D，E分别是边AC，AB的中点，连结BD.若BD平分∠ABC，则下列结论错误的是（ ）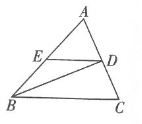
A、BC=2BE B、∠A=∠EDA C、BC=2AD D、BD⊥AC9. 如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判定四边形ABCD是平行四边形的是（ ）
A、AB∥DC，AD∥BC B、AB= DC，AD=BC C、AB∥DC，AD=BC D、OA=OC，OB=OD10. 平行四边形ABCD中，E，F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（ ）A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF二、填空题
-
11. 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED＝150°，则∠A的大小 ．
12. 如图，已知▱ABCD，AD⊥BD，AC=10，AD=4，则BD的长是.
13. 在 中， ，设 ，那么 的取值范围是14. 如图，在中，点D、E、F分别是各边的中点，若的面积为 ， 则的面积是.
15. 如图，平行四边形ABCD，对角线AC、BD相交于点O，点E是CD的中点， ，则AD的长是.
三、解答题
-
16. 如图，四边形ABCD是平行四边形，E为BC的中点，连接AE交DC延长线于点F．求证：DC＝CF．
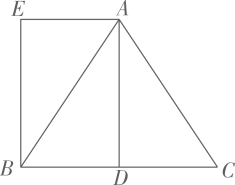
17. 已知：如图，在平行四边形ABCD中，E，F是对角线BD上的两点，且AE∥CF，求证：AE=CF。
18. 如图1，已知∠AOB，OA=OB，点E在OB上，且四边形AEBF是平行四边形，请用无刻度的直尺在图中画出∠AOB的平分线，小明的作法如图2，判断小明的作法是否正确，并说明理由。
19. 如图，▱ABCD的对角线AC，BD相交于点O，点E，点F在线段BD上，且DE＝BF．求证：AE∥CF．
