2022年江苏省淮安市中考数学模拟卷1

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共24分）

1. 在-3，0.3，0，- $\frac{1}{3}$ 这四个数中，绝对值最小的数是（）

A、-3 B、0.3 C、0 D、- $\frac{1}{3}$

查看试题解析
2. 今年的春晚继续拓展中央广播电视总台全媒体融合传播优势，刷新了跨媒体传播纪录.数据显示，春晚跨媒体受众总规模达12.72亿人.其中数据12.72亿用科学记数法表示为（）

A、 $12.72 \times 10^{8}$ B、 $0.1272 \times 10^{10}$ C、 $1.272 \times 10^{9}$ D、 $1.272 \times 10^{8}$

查看试题解析
3. 下列计算正确的是（）

A、 $x + x^{2} = x^{3}$ B、 $x^{2} \cdot x^{3} = x^{6}$ C、 $x^{6} \div x^{3} = x^{2}$ D、 ${(x^{2})}^{3} = x^{6}$

查看试题解析
4. 在下面的四个几何体中，主视图是三角形的是（）

A、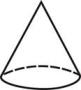圆锥 B、正方体 C、三棱柱 D、圆柱

查看试题解析
5. 下列事件中，属于必然事件的是（）

A、任意抛掷一只纸杯，杯口朝下 B、a为实数，｜a｜＜0 C、打开电视，正在播放动画片 D、任选三角形的两边，其差小于第三边

查看试题解析
6. 下面命题中，为真命题的是（）

A、内错角相等 B、一组对边平行，另一组对边相等的四边形是平行四边形 C、弧长相等的弧是等弧 D、平行于同一直线的两直线平行

查看试题解析
7. 如图，矩形ABCD中，AB=8cm，AD=6cm，EF是对角线BD的垂直平分线，则EF的长为（）cm．

A、 $\frac{15}{4}$ B、5 C、 $\frac{15}{2}$ D、8

查看试题解析
8. 我国古代数学著作《增删算法统宗》中有这么一首诗：“今有布绢三十疋，共卖价钞五百七．四疋绢价九十贯，三疋布价该五十．欲问绢布各几何？价钞各该分端的．若人算得无差讹，堪把芳名题郡邑．”其大意是：今有绵与布30疋，卖得570贯钱，4疋绢价90贯，3疋布价50贯，欲问绢布有多少，分开把价算，若人算得无差错，你的名字城镇到处扬．设有绢 $x$ 疋，布 $y$ 疋，依据题意可列方程组为（）

A、 ${\begin{matrix} x + y = 30 \\ \frac{50}{4} x + \frac{90}{3} y = 570 \end{matrix}$ B、 ${\begin{matrix} x + y = 30 \\ \frac{90}{4} x + \frac{50}{3} y = 570 \end{matrix}$ C、 ${\begin{matrix} x + y = 30 \\ \frac{90}{3} x + \frac{50}{4} y = 570 \end{matrix}$ D、 ${\begin{matrix} x + y = 30 \\ \frac{50}{3} x + \frac{90}{4} y = 570 \end{matrix}$

查看试题解析

二、填空题（每题3分，共24分）

9. 分解因式：a²﹣ab＝；

查看试题解析
10. 某校数学课外兴趣小组10个同学数学素养测试成绩如图所示，则该兴趣小组10个同学的数学素养测试成绩的众数是分.

查看试题解析
11. 分式方程 $\frac{1}{x - 2} + \frac{1 - x}{2 - x} = 3$ 的解是.

查看试题解析
12. 已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是.

查看试题解析
13. 已知三角形两边长分别是2和9，第三边的长为一元二次方程x²-14x+48=0的一个根，则这个三角形的周长为

查看试题解析
14. 正比例函数 $y_{1} = - 2 x$ 和反比例函数 $y_{2} = \frac{k}{x}$ 的图象都经过点A(-1， 2)，若 $y_{1} > y_{2}$ ，则x的取值范围是．

查看试题解析
15. 如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD＝56°，则∠BCD等于.

查看试题解析
16. 如图，点D为边长是 $4 \sqrt{3}$ 的等边△ABC边AB左侧一动点，不与点A，B重合的动点D在运动过程中始终保持∠ADB＝120°不变，则四边形ADBC的面积S的最大值是．

查看试题解析

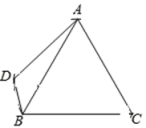
三、解答题（共11题，共102分）

17. 计算或解方程

(1)、 $| 2 - t a n 60 ° | - {(π - 3.14)}^{0} + {(- \frac{1}{2})}^{- 2} + \frac{1}{2} \sqrt{12}$ .

(2)、 $x^{2} - 6 x + 5 = 0$ （配方法）

查看试题解析
18. 先化简，再求值：（1 $- \frac{5}{x ＋ 2} ） \div \frac{x^{2} - 6 x ＋ 9}{x ＋ 2}$ ，其中x＝3 $- \sqrt{3}$ .

查看试题解析
19. 如图，四边形ABCD是平行四边形，E为BC的中点，连接AE交DC延长线于点F．求证：DC＝CF．

查看试题解析
20. 某校要加强中小学生作业、睡眠、手机、读物、体质管理．数学社团成员采用随机抽样的方法，抽取了七年级若干名学生，对他们一周内平均每天的睡眠时间t（单位：h）进行了调查，将数据整理后得到下列不完整的统计图表和扇形统计图：
请根据图表信息回答下列问题：

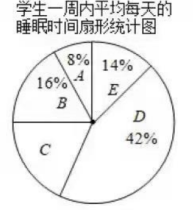
(1)、本次被抽取的七年级学生共有名；

(2)、统计图表中，m＝；

(3)、扇形统计图中，C组所在扇形的圆心角的度数是°；

(4)、请估计该校800名七年级学生中睡眠不足7小时的人数．

查看试题解析
21. 现有三张完全相同的不透明卡片。其正面分别写有数字-1，0，1，把这三张卡片背面朝上洗匀后放在桌面上。

(1)、随机的取一张卡片，求抽取的卡片的数字为负数的概率；

(2)、

先随机抽取一张卡片，其上的数字作为点A的横坐标；然后放回并洗匀，再随机抽取一张卡片，其上的数字作为A的纵坐标，试用画树状图或列表的方法求点A在抛物线 $y = x^{2}$ 上的概率.

查看试题解析
22. 如图，小马同学在数学综合实践活动中，利用所学的数学知识对山坡一棵树的高度进行测量，先测得小马同学离底部 $C$ 的距离 $B C$ 为10m，此时测得对树的顶端 $D$ 的仰角为55°，已知山坡与水平线的夹角为20°，小马同学的观测点 $A$ 距地面1.6m，求树木 $C D$ 的高度（精确到0.1m）．（参考数据： $\sin 55 ° \approx 0.82$ ， $\cos 55 ° \approx 0.57$ ， $\tan 55 ° \approx 1.43$ ， $\sin 20 ° \approx 0.34$ ， $\cos 20 ° \approx 0.94$ ， $\tan 20 ° \approx 0.36$ ）．

查看试题解析
23. 如图，已知 $△ A B C$ ．

(1)、请用尺规作图．在 $△ A B C$ 内部找一点 $P$ ，使得点 $P$ 到 $A B$ 、 $B C$ 、 $A C$ 的距离相等，（不写作图步骤，保留作图痕迹）；

(2)、若 $△ A B C$ 的周长为 $14 cm$ ，面积为 $\frac{21}{2} {cm}^{2}$ ，求点 $P$ 到 $A C$ 的距离．

查看试题解析
24. 如图，已知等边△ABC的边长为6，点O是AB边上的一点，以OA为半径的⊙O与边AC，AB分别交于点D，E，过点D作DF⊥BC于点F．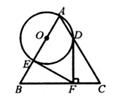

(1)、求证：DF是⊙O的切线；

(2)、连结EF，当EF是⊙O的切线时，求⊙O的半径．

查看试题解析
25. 某网店专售一款电动牙刷，其成本为20元/支，销售中发现，该商品每天的销售量y（支）与销售单价x（元/支）之间存在如图所示的关系．

(1)、求y与x的函数关系式；

(2)、该款电动牙刷销售单价定为多少元时，每天销售利润最大？最大利润是多少元？

查看试题解析
26. 如图，△ABC和△ADE是有公共顶点的直角三角形，∠BAC＝∠DAE＝90°，点P为射线BD，CE的交点．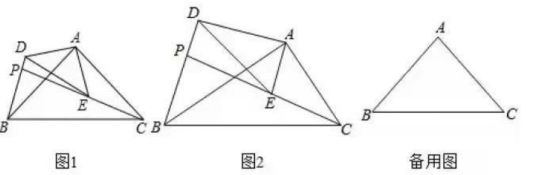

(1)、如图1，若△ABC和△ADE是等腰三角形，猜想∠ABD和∠ACE的数量关系是（），并说明理由；

(2)、如图2，若∠ADE＝∠ABC＝30°，则（1）中的结论是否仍然成立成立？请说明理由．

(3)、在（1）的条件下，AB＝6，AD＝4，若把△ADE绕点A旋转，当∠EAC＝90°时，请直接写出PB的长度．

查看试题解析
27. 如图，已知；抛物线y= $\frac{1}{4}$ x²+bx+c经过点A（0，2），点C（4，0），且交x轴于另一点B．

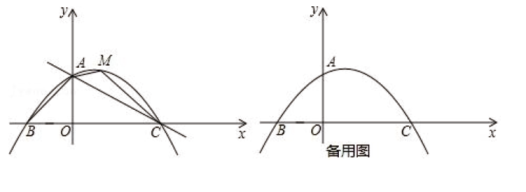(1)、求抛物线的解析式；

(2)、在直线AC上方的抛物线上有一点M，求三角形ACM面积的最大值及此时点M的坐标；

(3)、将线段OA绕x轴上的动点P（m，0）顺时针旋转90°得到线段O'A'，若线段O'A’与抛物线只有一个公共点，请结合函数图象，求m的取值范围．

查看试题解析