（人教版）2021-2022学年度第二学期八年级数学《勾股定理综合》复习卷

试卷更新日期：2022-04-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 有长为5cm，12cm的两根木条，现想找一根木条和这两根木条首尾顺次相连组成直角三角形，则下列木条长度适合的是（）

A、10cm B、13cm C、18cm D、20cm

查看试题解析
2. 如图，AB，BC，CD，DE是四根长度均为5cm的火柴棒，点A，C，E共线，若AC=6cm，CD⊥BC，则线段CE的长度是（）

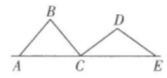A、6cm B、7cm C、6 $\sqrt{2}$ cm D、8cm

查看试题解析
3. 在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，如果 $A B = 8$ ， $B C = 6$ ，那么 $A C$ 的长是（）．

A、10 B、 $2 \sqrt{7}$ C、10或 $2 \sqrt{7}$ D、7

查看试题解析
4. 如图，作 $R t △ A B C$ ， $∠ C = 90 °$ ， $B C = 2 A C$ ；以A为圆心，以AC长为半径画弧，交斜边AB与点D；以B为圆心，以BD长为半径画弧，交BC与点E．若 $B C = 6$ ，则 $C E =$ （）

A、 $9 - 3 \sqrt{5}$ B、 $3 \sqrt{5} - 6$ C、 $3 \sqrt{5} - 3$ D、 $3 \sqrt{5} - 1$

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $B D ⊥ A C$ ，垂足为 $D$ ．如果 $A C = 6$ ， $B C = 3$ ，则 $B D$ 的长为（）

A、2 B、 $\frac{3}{2}$ C、 $3 \sqrt{3}$ D、 $\frac{3 \sqrt{3}}{2}$

查看试题解析
6. 如果下列各组数是三角形的三边，那么不能组成直角三角形的一组数是（）

A、9，40，41 B、5，12，13 C、0.3，0.4，0.5 D、8，24，25

查看试题解析
7. 满足下列条件的三角形中，不是直角三角形的是（）

A、三内角之比为3：4：5 B、三边长的平方之比为1：2：3 C、三边长之比为7：24：25 D、三内角之比为1：2：3

查看试题解析
8. 在如图所示的方格纸中，点A，B，C均为格点，则 $∠ A B C$ 的度数是（）

A、 $30 °$ B、 $35 °$ C、 $45 °$ D、 $60 °$

查看试题解析
9. 在△ABC中，点D在边BC上，若AD²+BD²＝AB² ，则下列结论正确的是（）

A、∠BAC＝90° B、∠BAD＝90° C、∠ABD＝90° D、∠ADB＝90°

查看试题解析
10. 下列条件：① $b^{2} = c^{2} - a^{2}$ ；② $∠ C = ∠ A - ∠ B$ ；③ $a ： b ： c = \frac{1}{3} ： \frac{1}{4} ： \frac{1}{5}$ ；④ $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ ，能判定 $△ A B C$ 是直角三角形的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 如图，已知△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形，且 $\frac{O A}{O A'}$ = $\frac{1}{2}$ .若点A的坐标为（-1，0），点C的坐标为（ $\frac{1}{2}$ ， 1），则A'C'=.

查看试题解析
12. 如图，在 $△$ ABC中，AB＝20，AC＝15，BC＝7，则点A到BC的距离是.

查看试题解析
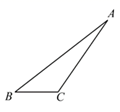13. 根据教材第65页“思考”栏目可以得到这样一个结论：如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，则AB＝2BC.请在这一结论的基础上继续思考：若AC＝2，点D是AB边上的动点，则CD+ $\frac{1}{2}$ AD的最小值为.

查看试题解析
14. 如图，校园内有一块长方形草地，为了满足人们的多样化品求，在草地内拐角位置开出了一条路，走此路可以省m的路．

查看试题解析
15. 如图所示的圆柱体中底面圆的半径是 $\frac{5}{π}$ ，高为12，若一只小虫从A点出发沿着圆柱体的侧面爬行到C点，CD、AB分别为上、下两底的直径，且 $C D ∥ A B$ ，则小虫爬行的最短路程是．

查看试题解析

三、解答题

16. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 15$ ， $A C = 20$ ， $A D ⊥ B C$ ，垂足为D.求AD，BD的长.

查看试题解析
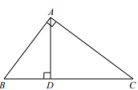17. 如图，在△ABC中，∠B＝45°，∠C＝30°，边AC的垂直平分线分别交边BC、AC于点D、E，DC＝6．求AB的长．

查看试题解析
18. 数学课上，老师出示了一个题：如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 5$ ， $A B = 13$ ， $∠ C A B$ 的平分线交CB于点D，求CD的长．
晓涵同学思索了一会儿，考虑到角平分线所在直线是角的对称轴这一特点，于是构造了一对全等三角形，解决了这个问题．请你在晓涵同学的启发下（或者独立思考后有自己的想法），解答这道题．

查看试题解析
19. “中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70千米/小时，如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路面对车速检测仪A正前方30米B处，过了2秒后，测得小汽车C与车速检测仪A间距离为50米，这辆小汽车超速了吗？

查看试题解析
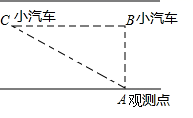20. 如图所示的一块空地进行草坪绿化，已知 AD＝4m ，CD＝3m，AD⊥DC，AB＝13m ，BC＝12m ，绿化草坪价格 150 元/米2。求这块地草坪绿化的价钱．

查看试题解析
21. 有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m的一棵大树上，大树高14m ，且巢离树顶部1m ．当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s ，那它至少需要多少时间才能赶回巢中？

查看试题解析
22. 《九章算术》是我国古代数学的经典著作.书中有一个“折竹抵地”问题：“今有竹高丈，未折抵地，间折者高几何？”意思是：一根柱子，原来高一丈（一丈为十尺），虫伤有病，一阵风将竹子折断，其竹梢恰好抵地，抵地处离原竹子根部三尺远，问：原处还有多高的竹子？

查看试题解析