（人教版）2021-2022学年度第二学期八年级数学《勾股定理》复习卷

试卷更新日期：2022-04-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 我国古代算书《九章算术》中第九章第六题是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深葭长各几何？你读懂题意了吗？请回答水深______尺，葭长_____尺.解：根据题意，设水深OB＝x尺，则葭长OA'＝（x+1）尺.可列方程正确的是（　　）

A、x²+5²＝（x+1）² B、x²+5²＝（x﹣1）² C、x²+（x+1）²＝10² D、x²+（x﹣1）²＝5²

查看试题解析
2. 如图， $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，D、E为BC边上两点， $∠ D A E = 45 °$ ，过A点作 $A F ⊥ A E$ ，且 $A F = A E$ ，连接DF、BF.下列结论：① $△ A B F ≌ △ A C E$ ，②AD平分 $∠ E D F$ ；③若 $B D = 4$ ， $C E = 3$ ，则 $A B = 6 \sqrt{2}$ ；④若 $A B = B E$ ， $S_{△ A B D} = \frac{1}{2} S_{△ A D E}$ ，其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在 $△ A B C$ 中， $A B = 10$ ， $A C = 17$ ，BC边上的高 $A D = 8$ ，则 $△ A B C$ 的面积为（）

A、72 B、84 C、36或84 D、72或84

查看试题解析
4. 如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于 $\frac{1}{2}$ MN长为半径画弧，两弧交于点O，作射线AO，交BC于点E．已知CE＝3，BE＝5，则AC的长为（）

A、8 B、7 C、6 D、5

查看试题解析
5. 如图，已知钓鱼竿 $A C$ 的长为 $10 m$ ，露在水面上的鱼线 $B C$ 长为 $6 m$ ，某钓鱼者想看看鱼钩上的情况，把鱼竿 $A C$ 转动到 $A C^{'}$ 的位置，此时露在水面上的鱼线 $B^{'} C^{'}$ 为 $8 m$ ，则 $B B^{'}$ 的长为（）

A、 $1 m$ B、 $2 m$ C、 $3 m$ D、 $4 m$

查看试题解析
6. 有一个边长为1的正方形，以它的一条边为斜边，向外作一个直角三角形，再分别以直角三角形的两条直角边为边，向外各作一个正方形，称为第一次“生长”（如图1）；再分别以这两个正方形的边为斜边，向外各自作一个直角三角形，然后分别以这两个直角三角形的直角边为边，向外各作一个正方形，称为第二次“生长”（如图2）……如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是（）

A、1 B、2020 C、2021 D、2022

查看试题解析
7. 如图，直线l上有三个正方形A、B、C，若正方形A、C的边长分别为4和6，则正方形B的面积为（）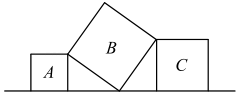

A、26 B、49 C、52 D、64

查看试题解析
8. 要焊接一个如图所示的钢架，需要的钢材长度是（）

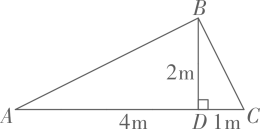A、 $(3 \sqrt{5} + 7) m$ B、 $(5 \sqrt{3} + 7) m$ C、 $(7 \sqrt{5} + 3) m$ D、 $(3 \sqrt{7} + 5) m$

查看试题解析
9. 如图，某超市为了吸引顾客，在超市门口离地高4.5m的墙上，装有一个由传感器控制的门铃A，如①图所示，人只要移至该门铃5m及5m以内时，门铃就会自动发出语音“欢迎光临”.如②图所示，一个身高1.5m的学生走到D处，门铃恰好自动响起，则BD的长为（）

A、3米 B、4米 C、5米 D、7米

查看试题解析
10. 如图，在数轴上点B表示的数为1，在点B的右侧作一个边长为1的正方形BACD，将对角线BC绕点B逆时针转动，使对角线的另一端落在数轴负半轴的点M处，则点M表示的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{2}$ +1 C、1﹣ $\sqrt{2}$ D、﹣ $\sqrt{2}$

查看试题解析

二、填空题

11. 如图，在 $△ A B C$ 中， $∠ A = 90 °$ ， $A B = A C$ ，点D为AB中点，过点B作 $B E ⊥ C D$ 交CD的延长线于点E，BE=2，CD=5，则DE= ．

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $A B = B C = 4$ ，以 $A B$ 为边作等边三角形 $A B D$ ，使点 $D$ 与点 $C$ 在 $A B$ 同侧，连接 $C D$ ，则 $C D =$ ．

查看试题解析
13. 如图，已知Rt△ABC，∠C=90°，BD是角平分线，BD=5，BC=4，则D点到AB的距离是。

查看试题解析
14. 在 $R t △ A B C$ 中， $∠ A = 90 ° ， B C = 10 ， A B = 6$ ，点P在AB上且P到另两边的距离相等，则 $A P$ 的长为.

查看试题解析
15. 直角三角形的两条边长分别为3cm、4cm，则这个直角三角形的斜边长为cm.

查看试题解析

三、解答题

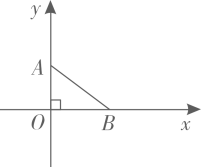
16. 如图，平面直角坐标系中，点A（0，3）和B（4，0），点M（8，m）为坐标平面内一动点，且△ABM为等腰三角形，求点M的坐标，

查看试题解析
17. 滑撑杆在悬窗中应用广泛.如图，某款滑撑杆由滑道 $O C$ ，撑杆 $A B$ 、 $B C$ 组成，滑道 $O C$ 固定在窗台上.悬窗关闭或打开过程中，撑杆 $A B$ 、 $B C$ 的长度始终保持不变.当悬窗关闭时，如图①，此时点A与点O重合，撑杆 $A B$ 、 $B C$ 恰与滑道 $O C$ 完全重合；当悬窗完全打开时，如图②，此时撑杆 $A B$ 与撑杆 $B C$ 恰成直角，即 $∠ B = 90 °$ ，测量得 $O A = 12 cm$ ，撑杆 $A B = 15 cm$ ，求滑道 $O C$ 的长度.

查看试题解析
18. 如图，在△ABC中，AD平分∠BAC.AB=AC=3，AD=2，求BC的长.

查看试题解析
19. 如图，△ABC中，∠ABC＝45°，F是高AD和高BE的交点，AC＝ $\sqrt{5}$ ， BD＝2．求线段DF的长度．

查看试题解析
20. 某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣．今天，他学到了勾股章第7题：“今有立木，系索其末，委地三尺，引索却行，去本八尺而索尽．问索长几何？”本题大意是：如图，木柱 $A B ⊥ B C$ ，绳索AC比木柱AB长三尺，BC的长度为8尺，求：绳索AC的长度．

查看试题解析
21. 一个25米长的梯子 $A B$ ，斜靠在一竖直的墙 $A O$ 上，这时的 $A O$ 距离为24米，如果梯子的顶端A沿墙下滑4米，那么梯子底端B外移多少米？

查看试题解析
22. 如图，在△ABC中，∠ADC＝∠BDC＝90°，AC＝20，BC＝15，BD＝9，求AD的长．

查看试题解析