黑龙江省齐齐哈尔市中考适应性模拟数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 在0.5,0,-1,-2这四个数中,相反数的倒数最大的数是( )A、0.5 B、0 C、-1 D、-22. 下列图形中,是中心对称的有( )
 A、1个 B、2个 C、3个 D、4个3. 下面的运算正确的是( )A、a+a2=a3 B、a2•a3=a5 C、6a﹣5a=1 D、a6÷a2=a34. 下列说法正确的是( )A、“清明时节雨纷纷”是必然事件 B、为了了解某小区居民新冠疫苗注射情况,可以采用普查的方式进行 C、一组数据2,5,4,5,6,7的众数、中位数和平均数都是5 D、甲、乙两组队员身高数据的方差分别为 , , 那么甲组队员的身高比较整齐5. 母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )A、3种 B、4种 C、5种 D、6种6. 李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )A、
A、1个 B、2个 C、3个 D、4个3. 下面的运算正确的是( )A、a+a2=a3 B、a2•a3=a5 C、6a﹣5a=1 D、a6÷a2=a34. 下列说法正确的是( )A、“清明时节雨纷纷”是必然事件 B、为了了解某小区居民新冠疫苗注射情况,可以采用普查的方式进行 C、一组数据2,5,4,5,6,7的众数、中位数和平均数都是5 D、甲、乙两组队员身高数据的方差分别为 , , 那么甲组队员的身高比较整齐5. 母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每支2元,百合每支3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )A、3种 B、4种 C、5种 D、6种6. 李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )A、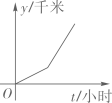 B、
B、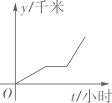 C、
C、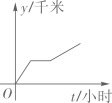 D、
D、 7. 若关于x的分式方程的解为正数,则m的取值范围是( ).A、m<-2且 B、m<2且 C、m>-3且 D、m>-3且8. 如图,某几何体的主视图和它的左视图,则搭建这样的几何体最少需要的小正方体为( )
7. 若关于x的分式方程的解为正数,则m的取值范围是( ).A、m<-2且 B、m<2且 C、m>-3且 D、m>-3且8. 如图,某几何体的主视图和它的左视图,则搭建这样的几何体最少需要的小正方体为( ) A、4个 B、5个 C、6个 D、7个9. 如图,正方形ABCD的边长为4,E是BC上一点,过点E作EF⊥AE,交DC于点F,连接AF,则AF的最小值是( )
A、4个 B、5个 C、6个 D、7个9. 如图,正方形ABCD的边长为4,E是BC上一点,过点E作EF⊥AE,交DC于点F,连接AF,则AF的最小值是( )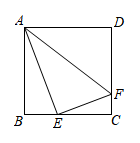 A、5 B、 C、 D、310. 如图是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac<b2 , ④a+b+c<0,⑤当x>0时,y随x的增大而减小,其中正确的是( )
A、5 B、 C、 D、310. 如图是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac<b2 , ④a+b+c<0,⑤当x>0时,y随x的增大而减小,其中正确的是( )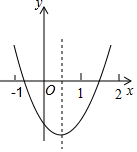 A、①②③ B、①②④ C、②③④ D、③④⑤
A、①②③ B、①②④ C、②③④ D、③④⑤二、填空题
-
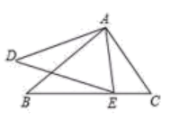
11. 某网店2022年母亲节这天的营业额为221000元,将数221000用科学记数法表示为 .12. 如图,如果∠BAD=∠CAE,那么添加条件 , 能确定△ABC和△ADE相似.
 13. 如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为1 cm,则这个扇形的半径是cm.
13. 如图,用一个圆心角为120°的扇形围成一个无底的圆锥,如果这个圆锥底面圆的半径为1 cm,则这个扇形的半径是cm.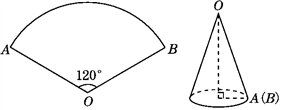 14. 如果关于x的不等式组 恰有2个整数解,则a的取值范围是.15. 在等边△ABC中,点D在BC边上,BD=3CD,连接AD,以AD为边作等边△ADE,连接CE,若CE=3,则AB的长为 .16. 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=kx(x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为
14. 如果关于x的不等式组 恰有2个整数解,则a的取值范围是.15. 在等边△ABC中,点D在BC边上,BD=3CD,连接AD,以AD为边作等边△ADE,连接CE,若CE=3,则AB的长为 .16. 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=kx(x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为
17. 如图,直线l: , 点坐标为(-3,0).过点作x轴的垂线交直线l于点 , 以原点O为圆心,长为半径画弧交x轴负半轴于点 , 再过点作x轴的垂线交直线l于点 , 以原点O为圆心,长为半径画弧交x轴负半轴于点 , …,按此做法进行下去,点的坐标为 .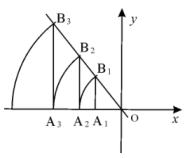
三、解答题
-
18. 计算及分解因式:(1)、 .(2)、19. .20. 小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:
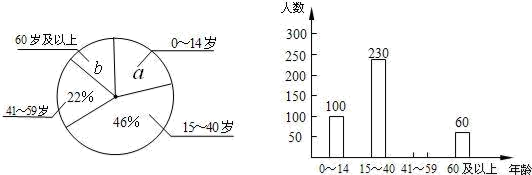
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)、小张同学共调查了名居民的年龄,扇形统计图中a=;(2)、补全条形统计图,并注明人数;(3)、若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为;(4)、若该辖区年龄在0~14岁的居民约有3500人,请估计该辖区居民人数是人.21. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.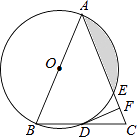 (1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.22. 2022年春节,某地连续14天进行了3次全员核酸检测.某次,甲乙两家医院对AB两个小区居民进行检测,在整个检测过程中,检测的人数y(人)与检测时间x(分)的对应关系如图所示:
(1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.22. 2022年春节,某地连续14天进行了3次全员核酸检测.某次,甲乙两家医院对AB两个小区居民进行检测,在整个检测过程中,检测的人数y(人)与检测时间x(分)的对应关系如图所示: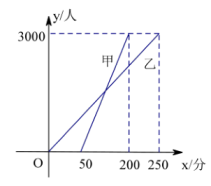 (1)、两家医院供检测人,甲乙两家医院检测的速度差是 .(2)、哪家医院先进行检测的?哪家医院先检测完?(3)、求出两家医院的y与x的函数关系式;(4)、甲医院开始检测多长时间两家医院检测人数相差200人?23. 实践与探究
(1)、两家医院供检测人,甲乙两家医院检测的速度差是 .(2)、哪家医院先进行检测的?哪家医院先检测完?(3)、求出两家医院的y与x的函数关系式;(4)、甲医院开始检测多长时间两家医院检测人数相差200人?23. 实践与探究情境:在正方形ABCD中,AB=5,点F在AC上,且 , 过点F作EF⊥AC,交CD于点E,连接AE,AF.
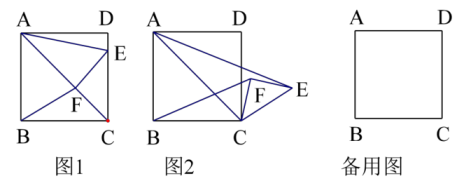 (1)、问题发现
(1)、问题发现图(1)中,线段AE与BF的数量关系是;
直线AE与直线BF的夹角的度数是 .
(2)、问题拓展当△CEF绕点C顺时针旋转时,(1)中的结论是否成立?若成立,请仅就图2的情形给出证明;若不成立,说明理由.
(3)、问题延伸在(2)的条件下,当点F到直线BC的距离为2时,直接写出AE的长.
24. 综合与探究如图,抛物线与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,对称轴与x轴交于点D,点P是直线BC上方抛物线上一点.
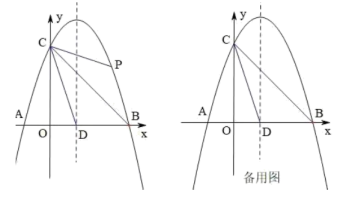 (1)、求抛物线的解析式;(2)、在直线BC上方的抛物线上找一点P,作PG⊥BC,当PG为最大值时,求线段PD的长;(3)、连接CD、CB,当∠PCB=∠DCB时,求点P的坐标.(4)、若点M为直线BC上一点,N为平面内一点,是否存在这样的点M和点N使得以C、D、M、N为顶点的四边形是菱形?若存在,直接写出点M坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、在直线BC上方的抛物线上找一点P,作PG⊥BC,当PG为最大值时,求线段PD的长;(3)、连接CD、CB,当∠PCB=∠DCB时,求点P的坐标.(4)、若点M为直线BC上一点,N为平面内一点,是否存在这样的点M和点N使得以C、D、M、N为顶点的四边形是菱形?若存在,直接写出点M坐标;若不存在,说明理由.