黑龙江省大庆市2022年九年级下学期第三次质量检测数学试题

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. -2019的相反数是（）

A、2019 B、-2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 近年来，国家高度重视精准扶贫，收效显著．据不完全统计6年间全国约有82000000人脱贫．数字82000000用科学记数法表示为（）

A、 $0.82 \times 1 0^{8}$ B、 $8.2 \times 1 0^{7}$ C、 $8.2 \times 1 0^{6}$ D、 $82 \times 1 0^{6}$

查看试题解析
3. 有理数a，b在数轴上的位置如图所示，则下列式子不正确的是（）

A、ab＜0 B、a+b＜0 C、|a|＜|b| D、a﹣b＜|a|+|b|

查看试题解析
4. 一组数据2，x，4，3，3的平均数是3，则这组数据的中位数、众数、方差分别是（　　）

A、3，3，0.4 B、2，3，2 C、3，2，0.4 D、3，3，2

查看试题解析
5. 有以下四个命题中，正确的命题是（）．

A、反比例函数 $y = - \frac{2}{x}$ ，当x>-2时，y随x的增大而增大 B、抛物线 $y = x^{2} - 2 x + 2$ 与两坐标轴无交点 C、垂直于弦的直径平分这条弦，且平分弦所对的弧 D、有一个角相等的两个等腰三角形相似

查看试题解析
6. 某几何体由若干个大小相同的小正方体搭成，其主视图与左视图如图所示，则搭成这个几何体的小正方体最少有（）

A、3个 B、5个 C、7个 D、9个

查看试题解析
7. 某商品原价为p元，由于供不应求，先提价10%进行销售，后因供应逐步充足，价格又一次性降价10%，则最后的实际售价为（）

A、p元 B、 $0.99 p$ 元 C、 $1.01 p$ 元 D、 $1.2 p$ 元

查看试题解析
8. 在同一平面直角坐标系中，函数y=mx+m与y= $\frac{m}{x}$ （m≠0）的图象可能是（）

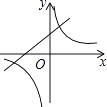A、 B、 C、 D、

查看试题解析
9. 如图，在△ABC中，AB＝AC＝4，∠BAC＝120°，M是BC的中点，点E是AB边上的动点，点F是线段BM上的动点，则ME+EF的最小值是（）

A、2 $\sqrt{2}$ B、3 C、4 D、2 $\sqrt{3}$

查看试题解析
10. 如图，在矩形ABCD中，AD＝ $\sqrt{2}$ AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①AE＝AD；②∠AED＝∠CED；③BH＝HF；④CF＝ $\sqrt{2}$ DF；⑤BC﹣CF＝2HE，其中正确的有（）

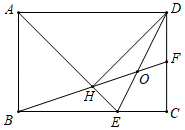A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

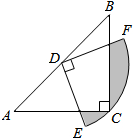
11. 已知圆锥底面积是30平方厘米，高是15厘米，则这个圆锥的体积为立方厘米．

查看试题解析
12. 函数 $y = \frac{2}{\sqrt{x + 1}}$ 的自变量x的取值范围是．

查看试题解析
13. 计算：若x+3y﹣2＝0，则2^x•8^y＝.

查看试题解析
14. 已知点 $A (a - 1 ， 2)$ 与点 $A^{'} (2 ， b + 1)$ 关于 $y$ 轴对称，则 $a + b$ 的值为.

查看试题解析
15. 已知 $\frac{2 x + 1}{(x - 3) (x + 4)} = \frac{A}{x - 3} + \frac{1}{x + 4}$ ，则 $A =$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $C A = C B = 4$ ， $∠ A C B = 90^{\circ}$ ，以AB中点D为圆心，作圆心角为 $90^{\circ}$ 的扇形DEF，点C恰好在弧EF上，则图中阴影部分面积为.

查看试题解析
17. 如图，在 $△ ABC$ 中， $AB = AC$ ， $∠ BAC = 52^{\circ}$ ， $∠ BAC$ 的平分线与AB的垂直平分线交于点O，将 $∠ C$ 沿EF折叠，若点C与点O恰好重合，则 $∠ OEC =$ .

查看试题解析
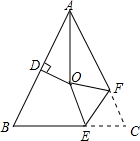18. 若t≤x≤t+2时，二次函数y＝2x²+4x+1的最大值为31，则t的值为．

查看试题解析

三、解答题

19. 计算： $\sqrt{12} - 2 \sin 60 ° + | 1 - \sqrt{3} | + 2019^{0}$ .

查看试题解析
20. 解方程： $\frac{x + 1}{x} + \frac{1}{x - 2}$ ＝1

查看试题解析
21. 已知a+b＝2，ab＝2，求 $\frac{1}{2}$ a³b+a²b²+ $\frac{1}{2}$ ab³的值.

查看试题解析
22. 如图，在一次户外研学活动中，老师带领学生去测一条东西流向的河流的宽度（把河两岸看做平行线，河宽即两岸之间的垂线段的长度）．某同学在河南岸A处观测到河对岸水边有一棵树P，测得P在A北偏东60°方向上，沿河岸向东前行20米到达B处，测得P在B北偏东45°方向上．求河宽（结果保留一位小数． $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）．

查看试题解析
23. 我市某中学艺术节期间，向全校学生征集书画作品．九年级美术王老师从全年级14个班中随机抽取了4个班，对征集到的作品的数量进行了分析统计，制作了如下两幅不完整的统计图．

(1)、王老师采取的调查方式是 ▲ （填“普查”或“抽样调查”），王老师所调查的4个班征集到作品共 ▲ 件，请把图（2）补充完整；

(2)、请估计全年级共征集到作品多少件？

(3)、如果全年级参展作品中有5件获得一等奖，其中有3名作者是男生，2名作者是女生．现在要在其中抽两人去参加学校总结表彰座谈会，请用列表或画树状图法求出恰好抽中一男一女的概率．

查看试题解析
24. 在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF//BC交BE的延长线于点F．

(1)、证明：四边形ADCF是菱形；

(2)、若AC＝3，AB＝4，求菱形ADCF的面积．

查看试题解析
25. 某服装专卖店计划购进A，B两种型号的精品女装．已知2件A型女装和3件B型女装共需5600元；1件A型女装和2件B型女装共需3400元．

(1)、求A，B型女装的单价．

(2)、专卖店购进A，B两种型号的女装共60件，其中A型的件数不少于B型件数的2倍，如果B型女装打八折，那么该专卖店至少需要准备多少贷款？

查看试题解析
26. 如图，一次函数y=kx+1与反比例函数y= $\frac{m}{x}$ （m≠0）相交于A、B两点，与x轴，y轴分别交于D、C两点，已知sin∠CDO= $\frac{\sqrt{5}}{5}$ ， △BOD的面积为1．

(1)、求一次函数和反比例函数的解析式；

(2)、连接OA，OB，点M是线段AB的中点，直线OM向上平移h（h＞0）个单位将△AOB的面积分成1：7两部分，求h的值．

查看试题解析
27. 如图，AB是⊙O的直径，弦CD⊥AB于H，G为⊙O上一点，连接AG交CD于K，在CD的延长线上取一点E，使EG＝EK，EG的延长线交AB的延长线于F．

(1)、求证：EF是⊙O的切线；

(2)、连接DG，若AC∥EF时．
①求证：KG²＝KD▪KE；
②若cosC＝ $\frac{4}{5}$ ， AK＝ $\sqrt{10}$ ，求BF的长．

查看试题解析
28. 如图1，在平面直角坐标系xOy中，直线l： $y = \frac{3}{4} x + m$ 与x轴、y轴分别交于点A和点B（0，﹣1），抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点B，且与直线l的另一个交点为C（4，n）.

(1)、求n的值和抛物线的解析式；

(2)、点D在抛物线上，且点D的横坐标为t（0＜t＜4）.DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）.若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；

(3)、M是平面内一点，将 $△$ AOB绕点M沿逆时针方向旋转90°后，得到 $△$ A₁O₁B₁ ，点A、O、B的对应点分别是点A₁、O₁、B₁.若 $△$ A₁O₁B₁的两个顶点恰好落在抛物线上，请直接写出点A₁的横坐标.

查看试题解析