河北省石家庄市十八县2022年3月份中考联考数学题

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，属于必然事件的是（）

A、打开电视正在播广告 B、射击运动员只射击1次，恰好命中靶心 C、一组数据的方差越小，则这组数据的波动越小 D、任意购买一张电影票，座位号是3的倍数

查看试题解析
3. 抛掷一枚质地均匀的硬币时，正面向上的概率是0.5．则下列判断正确的是（）

A、连续掷2次时，正面朝上一定会出现1次 B、连续掷100次时，正面朝上一定会出现50次 C、连续掷 $2 n$ 次时，正面朝上一定会出现 $n$ 次 D、当抛掷次数越大时，正面朝上的频率越稳定于0.5

查看试题解析
4. 如图是几何体的三视图，该几何体是（）

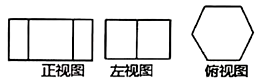A、圆锥 B、六棱锥 C、圆柱 D、六棱柱

查看试题解析
5. 如图， $Δ A B C$ 中， $∠ A B D = ∠ C$ ，若 $A B = 4$ ， $A D = 2$ ，则 $C D$ 边的长是（）

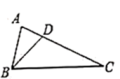A、2 B、4 C、6 D、8

查看试题解析
6. 从甲、乙、丙、丁四人中抽调两人参加“垃圾分类”志愿服务队，恰好抽到甲和丁的概率是（）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{1}{2}$ D、 $\frac{1}{8}$

查看试题解析
7. 如图，在4×4的网格图中，A、B、C是三个格点，其中每个小正方形的边长为1，△ABC的外心可能是（）

A、M点 B、N点 C、P点 D、Q点

查看试题解析
8. 如图，BC∥ED，下列说法不正确的是（）

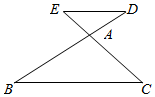A、两个三角形是位似图形 B、点A是两个三角形的位似中心 C、B与D、C与E是对应位似点 D、AE：AD是相似比

查看试题解析
9. 如图，小明在Р处测得A处的俯角为15°，B处的俯角为60°， $P B = 30 m$ ， $∠ P H B = ∠ A F B = 90 °$ ，若斜面AB坡度为 $1 ： \sqrt{3}$ ，则斜坡AB的长是（）

A、10m B、20m C、30m D、40m

查看试题解析
10. 关于反比例函数 $y = \frac{8}{x}$ ，下列说法不正确的是（）

A、函数图象分别位于第一、第三象限 B、函数图象关于原点中心对称 C、当 $x > 0$ 时， $y$ 随 $x$ 的增大而增大 D、当 $- 8 < x < - 1$ 时， $- 8 < y < - 1$

查看试题解析
11. 过点A用尺规作出直线MN的垂线AD，如图所示的作法中正确的是（）

A、①②③ B、②③④ C、①②④ D、①②③④

查看试题解析
12. 若关于二次函数 $y = (a - 1) x^{2} - 2 x + 2$ 的图象和x轴有交点，则a的取值范围为（）

A、 $a \leq \frac{3}{2}$ B、 $a \neq 1$ C、 $a < \frac{3}{2}$ 且 $a \neq 1$ D、 $a \leq \frac{3}{2}$ 且 $a \neq 1$

查看试题解析
13. 如图是一位同学从照片上剪切下来的海上日出时的画面，“图上”太阳与海平线交于A，B两点，他测得“图上”圆的半径为10厘米， $A B = 16$ 厘米．若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟，则“图上”太阳升起的速度为（）

A、1.0厘米/分 B、0.8厘米/分 C、1.2厘米/分 D、1.4厘米/分

查看试题解析
14. 如图，在平面直角坐标系中，矩形 $A B C D$ 四个顶点的坐标 $A (- 1 ， 2) ， B (- 1 ， - 1 ，) ， C (3 ， - 1) ， D (3 ， 2)$ ，当双曲线 $y = \frac{k}{x} (k > 0)$ 与矩形有四个交点时， $k$ 的取值范围是（）

A、 $0 < k < 2$ B、 $1 < k < 4$ C、 $k > 1$ D、 $0 < k < 1$

查看试题解析
15. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点坐标为（-1，n），其部分图象如图所示．以下结论不正确的是（）．

A、 $a b c > 0$ B、 $3 a + c > 0$ C、 $4 a c - b^{2} < 0$ D、关于 $x$ 的方程 $a x^{2} + b x + c = n + 1$ 无实数根

查看试题解析
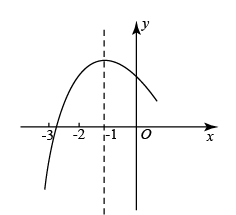16. 如图，在▱ABCD中，AE：DE=2：3，若AE的长为4，△AEF的面积为8，则下列结论：①BC=10；②AF•CF=EF•BF；③四边形CDEF的面积为62；④AD与BC之间的距离为14．其中正确的是（）

A、①②③ B、①③④ C、①②④ D、①②③④

查看试题解析

二、填空题

17. 计算： $\sqrt{8} - 2 c o s 45 ° =$ ．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 30 °$ ， $A B = 8$ ，将 $R t △ A B C$ 绕点C顺时针旋转得到 $R t △ A^{'} B^{'} C$ ，点B恰好在斜边 $A^{'} B^{'}$ 上，则线段CA扫过的面积为．则点A经过的路径的长为．

查看试题解析
19. 定义新运算：对于任意实数m，n都有 $m ☆ n = m^{2} - m n + n$ ，等式右边是常用的加法、减法、乘法及乘方运算．例如： $- 3 ☆ 2 = {(- 3)}^{2} - (- 3) \times 2 + 2 = 17$ ．根据以上知识解决问题：

(1)、若x☆3=1，则x的值为．

(2)、抛物线 $y = (2 - x) ☆ (- 1)$ 的顶点坐标是．

(3)、若 $2 ☆ a$ 的值小于0，则方程 $- 2 x^{2} - b x + a = 0$ 有个根．

查看试题解析

三、解答题

20. 如图，点 $A (1 ， - 3)$ 在反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上， $A M ⊥ x$ 轴于点M，点B是反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象上一动点，过点 $B$ 作 $B N ⊥ y$ 轴于点N．

(1)、求反比例函数的解析式．

(2)、连接MN，BM．小华说：“当 $x_{B} > \sqrt{3}$ 时， $S_{△ B M N}$ 随着 $x_{B}$ 的增大而减小．”你同意小华的说法吗?请说明理由．

查看试题解析
21. 图①是一辆登高云梯消防车的实物图，图②是其工作示意图，起重臂 $A C$ 是可伸缩的（ $10 m ⩽ A C ⩽ 20 m$ ），且起重臂 $A C$ 可绕点A在一定范围内转动，张角为 $∠ C A E (90 ° ⩽ ∠ C A E ⩽ 150 °)$ ，转动点A距离地面 $B D$ 的高度 $A E$ 为 $3.5 m$ ．

(1)、当起重臂 $A C$ 长度为 $12 m$ ，张角 $∠ C A E$ 为 $120 °$ 时，求云梯消防车最高点C距离地面的高度 $C F$ ；

(2)、某日、一居民家突发险情，该居民家距离地面的高度为 $18 m$ ，请问该消防车能否实施有效救援？（参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
22. 某校对九年级学生参与“力学”“热学”“光学”“电学”四个类别的物理实验情况进行了抽样调查，每位同学仅选其中一个类别，根据调查结果绘制了如图所示的不完整的频数分布表和扇形统计图（图1），请根据图表提供的信息，解答下列问题：
类别
频数（人数）
频率
力学
$m$
0.5
热学
8
光学
20
0.25
电学
12

(1)、求m的值．

(2)、求表示参与“热学”实验的扇形圆心角的度数．

(3)、参与“电学”实验的同学在做“灯泡亮了”的实验时，提出如下问题．
如图2，电路图上有四个开关A，B，C，D和一个小灯泡，闭合开关D或同时闭合开关A，B，C都可使小灯泡发光，若随机闭合其中的两个开关，用画树状图或列表的方法求小灯泡发光的概率．

查看试题解析
23. 古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”，它的完美来自对称．其中切弦（chord of contact）亦称切点弦，是一条特殊弦，从圆外一点向圆引两条切线，连接这两个切点的弦称为切弦．此时，圆心与已知点的连线垂直平分切弦．

(1)、为了说明切弦性质的正确性，需要对其进行证明．如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程．
已知：如图1，P是 $⊙ O$ 外一点， ▲ ．
求证： ▲ ．

(2)、如图2，在（1）的条件下，CD是 $⊙ O$ 的直径，连接AD，BC，若 $∠ A D C = 50 °$ ， $∠ B C D = 70 °$ ， $O C = 2$ ，求OP的长．

查看试题解析
24. 为实现农村经济可持续发展，石家庄市相关部门指导对口帮扶县区的村民，加工包装当地特色农产品进行销售，以增加村民收入．已知该特色农产品每件成本10元，日销售量y（袋）与每袋的售价x（元）之间关系如下表：
每袋的售价x（元）
…
20
30
…
日销售量y（袋）
…
20
10
…
如果日销售量y（袋）是每袋的售价x（元）的一次函数，请回答下列问题：

(1)、求日销售量y（袋）与每袋的售价x（元）之间的函数表达式；

(2)、求日销售利润P（元）与每袋的售价x（元）之间的函数表达式；

(3)、当每袋特色农产品以多少元出售时，才能使每日所获得的利润最大?最大利润是多少元?

查看试题解析
25. 如图，在菱形ABCD中， $∠ A B C$ 是锐角，点E是BC边上的动点（不与点B，C重合），将射线AE绕点A按逆时针方向旋转，交线段CD于点F．当 $∠ E A F = \frac{1}{2} ∠ B A D$ 时，延长线段BC交射线AF于点M，延长线段DC交射线AE于点N，连接AC．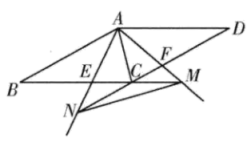

(1)、求证： $△ A N C ∽ △ M A C$ ；

(2)、连接MN，若 $A B = 4$ ， $A C = 2$ ，则当 $△ A M N$ 是以MN为腰的等腰三角形时，求CE的长．

查看试题解析
26. 如图，是某水上乐园为亲子游乐区新设滑梯的示意图，其中线段PA是竖直高度为6米的平台，PO垂直于水平面，滑道分为两部分，其中AB段是双曲线 $y = \frac{10}{x}$ 的一部分，BCD段是抛物线的一部分，两滑道的连接点B为抛物线的顶点，且B点的竖直高度为2米，滑道与水平面的交点D距PO的水平距离为7米．以点О为坐标原点建立平面直角坐标系，滑道上点的竖直高度为y，距直线PO的水平距离为x．

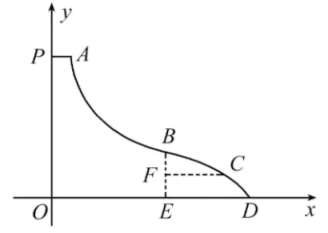(1)、请求出滑道BCD段y与x之间的函数关系式；

(2)、当滑行者滑到C点时，距地面的距离为1米，求滑行者此时距滑道起点A的水平距离；

(3)、在建模实验中发现，为保证滑行者的安全，滑道BCD落地点D与最高点B连线与水平面夹角应不大于45°，且由于实际场地限制， $\frac{O P}{O D} \geq \frac{1}{2}$ ，求OD长度的取值范围．

查看试题解析

类别	频数（人数）	频率
力学	$m$	0.5
热学	8
光学	20	0.25
电学	12

每袋的售价x（元）	…	20	30	…
日销售量y（袋）	…	20	10	…