广东省珠海市2022年九年级下学期数学第二次模拟试题

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. -5 的相反数是（）

A、-5 B、 $- \frac{1}{5}$ C、 $\frac{1}{5}$ D、5

查看试题解析
2. 现有一组数据3，4，6，5，5，则这组数据的中位数是（）

A、6 B、5 C、4 D、3

查看试题解析
3. 点P（a，﹣4）与Q（2，4）关于x轴对称，则a的值为（）

A、﹣6 B、﹣2 C、2 D、6

查看试题解析
4. 如果一个正多边形的内角和是900°，则这个正多边形是（）

A、正七边形 B、正九边形 C、正五边形 D、正十边形

查看试题解析
5. 函数 $y = \frac{\sqrt{x + 3}}{x - 2}$ 中，自变量x的取值范围是（）

A、 $x > - 3$ B、 $x \geq - 3$ 且 $x \neq 2$ C、 $x \neq 2$ D、 $x > - 3$ 且 $x \neq 2$

查看试题解析
6. 如图，在△ABC中， $B C$ 的垂直平分线交 $A C$ ， $B C$ 于点 $D$ ， $E$ ．若△ABC的周长为30， $B E = 5$ ，则△ABD的周长为（）

A、10 B、15 C、20 D、25

查看试题解析
7. 如果不等式组 ${\begin{array}{l} \frac{x}{3} ＜ 1 - \frac{x - 3}{6} \\ x ＜ m \end{array}$ 的解集是x＜3，那么m的取值范围是（）

A、m＜ $\frac{7}{8}$ B、m≥ $\frac{7}{8}$ C、m＜3 D、m≥3

查看试题解析
8. 如图，A是反比例函数y＝ $\frac{k}{x}$ 的图象上一点，点C在x轴上，且S_△ABC＝2，则k的值为（）

A、4 B、﹣4 C、﹣2 D、2

查看试题解析
9. 如图，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=60°，则∠AED′=（）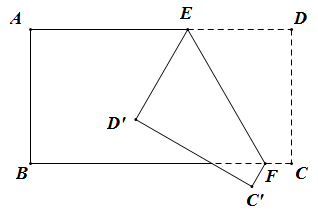

A、50° B、55° C、60° D、65°

查看试题解析
10. 如图，已知点A（ $\sqrt{3}$ ，2）， B(0，1)，射线AB绕点A逆时针旋转30°，与x轴交于点C，则过A，B，C三点的二次函数y=ax²+bx+1中a，b的值分别为（）

A、 $a = 2 ， b = - \frac{5}{3} \sqrt{3}$ B、 $a = \frac{1}{2} ， b = - \frac{\sqrt{3}}{6}$ C、 $a = 3 ， b = - \frac{8}{3} \sqrt{3}$ D、 $a = - \frac{1}{3} ， b = \frac{2}{3} \sqrt{3}$

查看试题解析

二、填空题

11. 分解因式：a²﹣2ab＝．

查看试题解析
12. 若 $- \frac{1}{3} a^{x + y} b^{3}$ 与 $2 a^{3} b^{y}$ 是同类项，则 $y - x =$ ．

查看试题解析
13. 若x、y为实数，且|x＋3|＋ $\sqrt{y - 3}$ ＝0，则（ $\frac{x}{y}$ ）²⁰²¹的值为．

查看试题解析
14. 若x²+2x的值是6，则2x²+4x﹣7的值是．

查看试题解析
15. 如图，在△ABC中，∠B=30°，∠C=50°，通过观察尺规作图的痕迹，∠DAE的度数是．

查看试题解析
16. 如图，圆锥的高AO＝4，底面圆半径为3，则圆锥的侧面积为．

查看试题解析
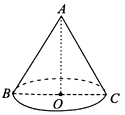17. 如图所示，设G是△ABC的重心，过G的直线分别交AB，AC于点P，Q两点，则 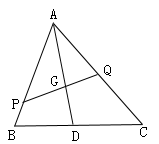$\frac{P B}{P A} + \frac{Q C}{Q A}$ =.

查看试题解析

三、解答题

18. 先化简，再求值： ${(2 a - 3 b)}^{2} ﹣ (3 b + a) (3 b - a)$ ，其中a= $\sqrt{2}$ ， $b = \sqrt{3}$ ．

查看试题解析
19. 某中学号召学生开展社会实践活动．学校随机地通过问卷形式调查了200名学生，并将学生参加社会实践活动的天数，绘制了如下不完整的条形统计图：
请根据图中提供的信息，完成下列问题（填入结果和补全图形）：

(1)、补全条形统计图；

(2)、学生参加社会实践活动天数的中位数是天；学生参加社会实践活动天数的众数是天；

(3)、该校共有1500人，请你估计“实践活动时间为5天”的学生有多少人？

查看试题解析
20. 如图， $△ A B E ≌ △ D C E$ ，点E在线段 $A D$ 上，点F在 $C D$ 延长线上， $∠ F = ∠ A$ ，求证： $A D ∥ B F$ ．

查看试题解析
21. 已知关于x的一元二次方程x²-4x+k-1=0有实数根．

(1)、求k的取值范围；

(2)、若此方程的两实数根x₁ ， x₂满足x₁²+x₂²=10，求k的值．

查看试题解析
22. 有甲、乙两种客车，2辆甲种客车与3辆乙种客车的总载客量为170人，1辆甲种客车与2辆乙种客车的总载客量为100人．

(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人？

(2)、某单位组织180名员工到某革命家传统教育基地开展“纪念建党100周年”活动，拟租用甲、乙两种客车共5辆，总费用在1950元的限额内，一次将全部员工送到指定地点．若每辆甲种客车的租金为400元，每辆乙种客车的租金为320元，有哪几种租车方案，最少租车费用是多少？

查看试题解析
23. 如图，在平面直角坐标系中，矩形ABCD的顶点A，B在x轴的正半轴上，顶点D在直线y＝ $\frac{3}{2}$ x位于第一象限的图象上，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过点D，交BC于点E，AB＝4．

(1)、如果BC＝6，求点E的坐标；

(2)、连接DE，当DE⊥OD时，求点D的坐标．

查看试题解析
24. 如图1，在正方形ABCD中，AB＝10，点O，E在边CD上，且CE＝2，DO＝3，以点O为圆心，OE为半径在其左侧作半圆O，分别交AD于点G，交CD的延长线于点F．

(1)、AG＝；

(2)、如图2，将半圆O绕点E逆时针旋转α（0°＜α＜180°），点O的对应点为O′，点F的对应点为F′，设M为半圆O′上一点．
①当点F′落在AD边上时，求点M与线段BC之间的最短距离；

②当半圆O′交BC于P，R两点时，若 $\overset{⏜}{P R}$ 的长为 $\frac{5}{3}$ π，求此时半圆O′与正方形ABCD重叠部分的面积；

③当半圆O′与正方形ABCD的边相切时，设切点为N，直接写出tan∠END的值．

查看试题解析
25. 如果抛物线C₁的顶点在抛物线C₂上，抛物线C₂的顶点也在抛物线C₁上时，那么我们称抛物线C₁与C₂“互为关联”的抛物线．如图1，已知抛物线C₁：y₁＝ $\frac{1}{4}$ x²+x与C₂：y₂＝ax²+x+c是“互为关联”的抛物线，点A，B分别是抛物线C₁ ， C₂的顶点，抛物线C₂经过点D（6，﹣1）．

(1)、直接写出A，B的坐标和抛物线C₂的解析式；

(2)、抛物线C₂上是否存在点E，使得△ABE是直角三角形？如果存在，请求出点E的坐标；如果不存在，请说明理由；

(3)、如图2，点F（﹣6，3）在抛物线C₁上，点M，N分别是抛物线C₁ ， C₂上的动点，且点M，N的横坐标相同，记△AFM面积为S₁（当点M与点A，F重合时S₁＝0），△ABN的面积为S₂（当点N与点A，B重合时，S₂＝0），令S＝S₁+S₂ ，观察图象，当y₁≤y₂时，写出x的取值范围，并求出在此范围内S的最大值．

查看试题解析