广东省广州市天河区2022年一模数学试题

试卷更新日期：2022-04-18 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的相反数是（）

A、 -3 B、 $3$ C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下列是四届冬奥会会徽的部分图案，其中既是轴对称图形，又是中心对称图形的是（）.

A、1984前南斯拉夫 B、1988加拿大 C、2006意大利 D、2022中国

查看试题解析
3. 下列式子运算正确的是（）.

A、3x + 4x = 7x² B、 ${(x^{2} y)}^{3} = x^{2} y^{3}$ C、x³·x⁴ = x⁷ D、 $(x^{3})^{4} = x^{7}$

查看试题解析
4. 如图，将 $Δ$ ABC绕点A逆时针方向旋转得到△AB′C′.当点B′刚好落在BC边上，∠B = 40°，则∠BAB′的度数为（）.

A、120° B、100° C、80° D、60°

查看试题解析
5. 小明参加校园歌手比赛，唱功得85分，音乐常识得95分，综合知识得90分，学校如果按如图所示的权重计算总评成绩，那么小明的总评成绩是（）

A、87分 B、87.5分 C、88.5分 D、89分

查看试题解析
6. 如图，在平行四边形ABCD中，E，F分别在边BC，AD上，添加选项中的条件后不能判定四边形AECF是平行四边形的是（）.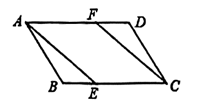

A、BE = DF B、AE $/ /$ CF C、AF = EC D、AE = EC

查看试题解析
7. 一元二次方程 $x^{2} + x + k = 0$ 有两个相等的实数根，则 $\sqrt{k + 1}$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{2}$ C、 $\frac{5}{4}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
8. 如图，在平面直角坐标系中，O是坐标原点，在 $Δ O A B$ 中， $A O = A B$ ， $A C ⊥ O B$ 于点C，点A在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，若 $O B = 4$ ， $A C = 3$ ，则k的值为（）．

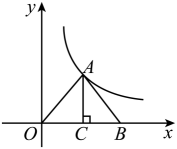A、12 B、8 C、6 D、3

查看试题解析
9. 如图，每个小正方形的边长为1，在△ABC中，点D为AB的中点，则线段CD的长为（）

A、 $\sqrt{13}$ B、 $\frac{\sqrt{26}}{2}$ C、 $2 \sqrt{2}$ D、 $\sqrt{10}$

查看试题解析
10. 已知二次函数y = x² - x + $\frac{\sqrt{2}}{8}$ ，若x = a时，y < 0：则当x = a - 1时，对应的函数值范围判断合理的是（）.

A、y < 0 B、0 < y < $\frac{\sqrt{2}}{8}$ C、 $\frac{\sqrt{2}}{8}$ < y < $\frac{16 + \sqrt{2}}{8}$ D、y > $\frac{4 + \sqrt{2}}{8}$

查看试题解析

二、填空题

11. 代数式 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 计算： $\frac{\sqrt{2}}{\sqrt{3}}$ =

查看试题解析
13. 因式分解：3ax - 9ay = .

查看试题解析
14. 一次函数 $y = (1 - k) x + k^{2} - 1$ 的图象经过原点，则y随x的增大而 .（填“增大”或“减小”）

查看试题解析
15. 如图所示，在正方形ABCD中，点P在AC上， $P E ⊥ A B$ ， $P F ⊥ B C$ ，垂足分别为E，F， $E F = 3$ ，则DP的长为．

查看试题解析
16. 如图，BD为⊙O的直径，点A是弧BC的中点，AD交BC于E点，⊙O的切线DF与BC的延长线交于点F， $A E = 2$ ， $E D = 4$ ．则

(1)、 $s i n ∠ A D B =$ ；

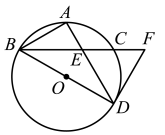(2)、下列四个结论中正确的有（填写序号）．
① $Δ A B E ∽ Δ A D B$ ；②AB=4；
③ $\overset{⌢}{A B}$ 的长 $= \frac{\sqrt{3}}{3} π$ ；④CF=AE．

查看试题解析

三、解答题

17. 解方程组： ${\begin{array}{l} x - y = 2 \\ x + y = 4 \end{array}$

查看试题解析
18. 如图，已知AB∥DE，AB = DE，B，E，C，F在同一条直线上，且BE = CF．
求证∶△ABC≌△DEF．

查看试题解析
19. 已知代数式T = （ $\frac{b}{a}$ - $\frac{a}{b}$ ） ÷ $\frac{a + b}{b}$ .若点A（a，b）在直线 y= 3x上，求T的值.

查看试题解析
20. 为庆祝中国共产党成立100周年，某校举行“学党史·感党恩”知识竞答活动.甲、乙两班各选出5名学生参加竞赛，其竞赛成绩（满分为100分）如表所示：
甲班
1号
2号
3号
4号
5号

80分
80分
80分
100分
90分
乙班
6号
7号
8号
9号
10号

80分
100分
85分
70分
95分

(1)、写出甲、乙两个班这10名学生竞赛成绩的中位数和众数：

(2)、若从甲、乙两班竞赛成绩“≥90分”的4名学生中随机抽取2名参加全区党史知识竞赛，求这2名学生恰好来自同一个班的概率.

查看试题解析
21. 如图，线段AD是△ABC的角平分线.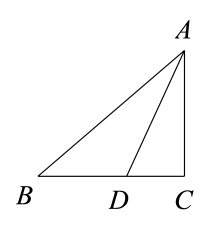

(1)、尺规作图：作线段AD的垂直平分线分别交AB，AC于点E，F：（保留痕迹，不写作法）

(2)、在（1）所作的图中，连接DE，DF，求证：四边形AEDF是菱形.

查看试题解析
22. 看电影已经成为人们在春节假期生活的新热潮.2022年春节电影总票房持续走高，其中《长津湖》《四海》和《奇迹》三部电影七天票房总额达到37亿元.

(1)、若《四海》的票房比《奇迹》的票房少2亿，《长津湖》的票房比《奇迹》的票房的3倍多4亿，求电影《长津湖》的票房；

(2)、若电影院票价每张60元，学生实行半价优惠.某学校计划用不超过1500元组织老师和学生共40名去电影院观看《长津湖》，问：至少组织多少名学生观看电影?

查看试题解析
23. 如图，在平面直角坐标系中，直线y= x与双曲线 $y = \frac{k}{x}$ 交于A，B两点，其中A的坐标为（1，a），P是以点C（ - 2，2）为圆心，半径长为1的圆上一动点，连接AP，Q为AP的中点.

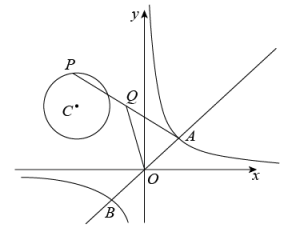(1)、求双曲线的解析式：

(2)、将直线y = x向上平移m（m > 0）个单位长度，若平移后的直线与⊙C相切，求m的值

(3)、求线段OQ长度的最大值.

查看试题解析
24. 如图，在矩形ABCD中，AB = 6，AD = 8，点E是CD边上的一个动点（点E不与点C重合），延长DC到点F，使EC = 2CF，且AF与BE交于点G.

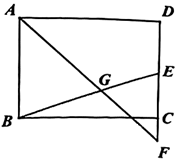(1)、当EC = 4时，求线段BG的长：

(2)、设CF = x，△GEF的面积为y，求y与x的关系式，并求出y的最大值：

(3)、连接DG，求线段DG的最小值.

查看试题解析
25. 若抛物线y = ax² + bx + c（a，b，c是常数，c > 1）过点A（c，0），且0 < x < c时，总有y > 0．

(1)、当a = c = 2，求b的值；

(2)、当a = $\frac{1}{4}$ 时，求该抛物线顶点纵坐标的取值范围；

(3)、当a > 0，x > 0时，求证∶ax（x + 1）+ bx（x + 2）+ c（x + 1)(x + 2）> 0．

查看试题解析

甲班	1号	2号	3号	4号	5号
	80分	80分	80分	100分	90分
乙班	6号	7号	8号	9号	10号
	80分	100分	85分	70分	95分