广东省珠海市2022年九年级下学期第一次模拟监测数学试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 2022的相反数是( )A、﹣2022 B、2022 C、 D、﹣2. 防疫工作一刻都不能放松,截至2021年4月4日22时,全球累计确诊感染新冠肺炎约为1.3亿人,将数字130000000用科学记数法表示为( ).A、 B、 C、 D、3. 如图是由8个完全相同的小正方体组成的一个立体图形,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 信息技术课上,在老师的指导下,小好同学训练打字速度(字/min),数据整理如下:15,17,23,15,17,17,19,21,21,18,对于这组数据,下列说法正确的是( )A、众数是17 B、众数是15 C、中位数是17 D、中位数是185. 下列运算正确的是( )A、 B、 C、 D、6. 下列关于x的一元二次方程中,有两个相等的实数根的方程是( )A、 B、 C、 D、7. 如图, , , 平分 , 则的度数为( )
4. 信息技术课上,在老师的指导下,小好同学训练打字速度(字/min),数据整理如下:15,17,23,15,17,17,19,21,21,18,对于这组数据,下列说法正确的是( )A、众数是17 B、众数是15 C、中位数是17 D、中位数是185. 下列运算正确的是( )A、 B、 C、 D、6. 下列关于x的一元二次方程中,有两个相等的实数根的方程是( )A、 B、 C、 D、7. 如图, , , 平分 , 则的度数为( )
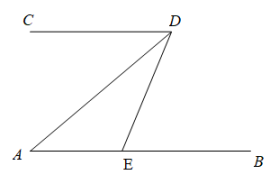 A、 B、 C、 D、8. 如图,CD是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在AC边上,若 ,则 的长为( )
A、 B、 C、 D、8. 如图,CD是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在AC边上,若 ,则 的长为( ) A、 B、 C、 D、9. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )
A、 B、 C、 D、9. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )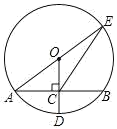 A、2 B、8 C、2 D、210. 二次函数 的图象如图所示.下列结论:① ;② ;③m为任意实数,则 ;④ ;⑤若 且 ,则 .其中正确结论的个数有( )
A、2 B、8 C、2 D、210. 二次函数 的图象如图所示.下列结论:① ;② ;③m为任意实数,则 ;④ ;⑤若 且 ,则 .其中正确结论的个数有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 点A(5,-3)向左平移3个单位,再向下平移2个单位后的坐标是12. 函数关系式y有意义,则x的取值范围是 .13. 因式分解: .14. 二元一次方程组 的解为 .15. 如图,在中,点、分别在边、上, , 如果 , , 那么的长是 .
 16. 如图,AB为⊙O的直径, AB=4,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点O,则劣弧AC的弧长是 .
16. 如图,AB为⊙O的直径, AB=4,点C为圆上一点,将劣弧AC沿弦AC翻折交AB于点O,则劣弧AC的弧长是 . 17. 如图,直线l为y=x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为 .
17. 如图,直线l为y=x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1 , 以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2 , 以原点O为圆心,OB2长为半径画圆弧交x轴于点A3;……,按此作法进行下去,则点An的坐标为 .
三、解答题
-
18. 计算:19. 如图,在Rt△ABC中,∠C=90°.
 (1)、作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).(2)、在(1)的条件下,若∠BAC=28°,求∠ADB的度数.20. 课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示:
(1)、作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).(2)、在(1)的条件下,若∠BAC=28°,求∠ADB的度数.20. 课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示: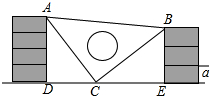 (1)、求证:;(2)、假设砌墙所用的每块砖块的厚度相同,请你帮小明求出的值.21. 从2021年秋季开学以来,全国各地中小学都开始实行了“双减政策”.为了解家长们对“双减政策”的了解情况,从某校1200名家长中随机抽取部分家长进行问卷调查,调直评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类,并根据调查结果绘制出如图所示的两幅不完整的统计图.
(1)、求证:;(2)、假设砌墙所用的每块砖块的厚度相同,请你帮小明求出的值.21. 从2021年秋季开学以来,全国各地中小学都开始实行了“双减政策”.为了解家长们对“双减政策”的了解情况,从某校1200名家长中随机抽取部分家长进行问卷调查,调直评价结果分为“了解较少”“基本了解”“了解较多”“非常了解”四类,并根据调查结果绘制出如图所示的两幅不完整的统计图. (1)、本次抽取家长共有人,扇形图中“基本了解”所占扇形的圆心角是;(2)、估计此校“非常了解”和“了解较多”的家长共有多少人?(3)、学校计划从“了解较少”的家长中抽取1位初一学生家长,1位初二学生家长,2位初三学生家长参加培训,若从这4位家长中随机选取两人作为代表,请通过列表或面树状图的方法求所选出的两位家长既有初一家长,又有初二家长的概率.22. 已知反比例函数的图象与一次函数的图象交于点A(1,4)和点B( , -2).
(1)、本次抽取家长共有人,扇形图中“基本了解”所占扇形的圆心角是;(2)、估计此校“非常了解”和“了解较多”的家长共有多少人?(3)、学校计划从“了解较少”的家长中抽取1位初一学生家长,1位初二学生家长,2位初三学生家长参加培训,若从这4位家长中随机选取两人作为代表,请通过列表或面树状图的方法求所选出的两位家长既有初一家长,又有初二家长的概率.22. 已知反比例函数的图象与一次函数的图象交于点A(1,4)和点B( , -2). (1)、求m的值及一次函数的关系式;(2)、求△OAB的面积;(3)、当时,求的取值范围.23. 戴口罩可以有效降低感染新型冠状病毒的风险.某学校在本学期开学初为九年级学生购买A、B两种口罩,经过市场调查, A的单价比B的单价少2元,花费450元购买A口罩和花费750元购买B口罩的个数相等.(1)、求A、B两种口罩的单价;(2)、若学校需购买两种口罩共500个,总费不超过2100元,求该校本次购买A种口罩最少有多少个?24. 如图,在中, , D为AB边上的一点,以AD为直径的交BC于点E,交AC于点F,过点C作于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为的切线.
(1)、求m的值及一次函数的关系式;(2)、求△OAB的面积;(3)、当时,求的取值范围.23. 戴口罩可以有效降低感染新型冠状病毒的风险.某学校在本学期开学初为九年级学生购买A、B两种口罩,经过市场调查, A的单价比B的单价少2元,花费450元购买A口罩和花费750元购买B口罩的个数相等.(1)、求A、B两种口罩的单价;(2)、若学校需购买两种口罩共500个,总费不超过2100元,求该校本次购买A种口罩最少有多少个?24. 如图,在中, , D为AB边上的一点,以AD为直径的交BC于点E,交AC于点F,过点C作于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为的切线. (1)、求证:BC是的切线;(2)、求证:AE平分;(3)、若 , , , 求四边形CHQE的面积.25. 如图1,抛物线经过点A(4,3),对称轴是直线=2,顶点为B.抛物线与轴交于点C,连接AC,过点A作AD⊥轴于点D,点E是线段AC上的动点(点E不与A、C两点重合).
(1)、求证:BC是的切线;(2)、求证:AE平分;(3)、若 , , , 求四边形CHQE的面积.25. 如图1,抛物线经过点A(4,3),对称轴是直线=2,顶点为B.抛物线与轴交于点C,连接AC,过点A作AD⊥轴于点D,点E是线段AC上的动点(点E不与A、C两点重合). (1)、求抛物线的函数解析式和顶点B的坐标;(2)、若直线BE将四边形ACOD分成面积比为1:3的两个四边形,求点E的坐标;(3)、如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在轴上的同时点F也恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.
(1)、求抛物线的函数解析式和顶点B的坐标;(2)、若直线BE将四边形ACOD分成面积比为1:3的两个四边形,求点E的坐标;(3)、如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在轴上的同时点F也恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.