广东省深圳市坪山区2022年中考数学一模试题
试卷更新日期:2022-04-18 类型:中考模拟
一、单选题
-
1. 如图,该几何体的左视图是( )
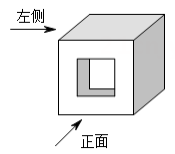 A、
A、 B、
B、 C、
C、 D、
D、 2. 一元二次方程x2﹣x﹣1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断3. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、-4 C、2 D、-24. 解一元二次方程x2﹣2x=4,配方后正确的是( )A、(x+1)2=6 B、(x﹣1)2=5 C、(x﹣1)2=4 D、(x﹣1)2=85. 在平面直角坐标系中,将抛物线y=x2向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是( )A、y=(x﹣1)2+2 B、y=(x﹣1)2﹣2 C、y=(x+1)2﹣2 D、y=(x+1)2+26. 如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为 时,标准视力表中最大的“
2. 一元二次方程x2﹣x﹣1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断3. 若 与 都是反比例函数 图象上的点,则a的值是( )A、4 B、-4 C、2 D、-24. 解一元二次方程x2﹣2x=4,配方后正确的是( )A、(x+1)2=6 B、(x﹣1)2=5 C、(x﹣1)2=4 D、(x﹣1)2=85. 在平面直角坐标系中,将抛物线y=x2向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是( )A、y=(x﹣1)2+2 B、y=(x﹣1)2﹣2 C、y=(x+1)2﹣2 D、y=(x+1)2+26. 如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为 时,标准视力表中最大的“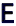 ”字高度为 ,当测试距离为 时,最大的“
”字高度为 ,当测试距离为 时,最大的“ 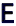 ”字高度为( )mm
”字高度为( )mm 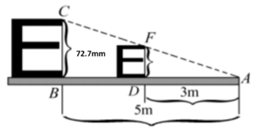 A、4.36 B、29.08 C、43.62 D、121.177. 如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )
A、4.36 B、29.08 C、43.62 D、121.177. 如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )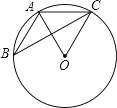 A、30° B、45° C、60° D、70°8. 下列命题:
A、30° B、45° C、60° D、70°8. 下列命题:①有一个角等于100°的两个等腰三角形相似;②对角线互相垂直的四边形是菱形;③一个角为90°且一组邻边相等的四边形是正方形;④对角线相等的平行四边形是矩形.
其中真命题的个数是( )
A、1 B、2 C、3 D、49. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=bx+c在同一坐标系内的大致图象是( ) A、
A、 B、
B、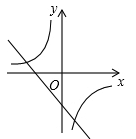 C、
C、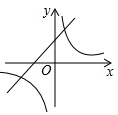 D、
D、 10. 如图,△ABC中,∠ABC=45°,BC=4,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )
10. 如图,△ABC中,∠ABC=45°,BC=4,tan∠ACB=3,AD⊥BC于D,若将△ADC绕点D逆时针方向旋转得到△FDE,当点E恰好落在AC上,连接AF.则AF的长为( )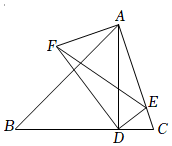 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
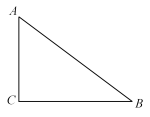
11. 方程x2﹣2x=0的解为 .12. 如图,在中, , , , 则的值是 .
 13. 一个不透明的布袋里装有3个只有颜色不同的球,其中1个红球,2个白球,从布袋里摸出1个球,则摸到的球是红球的概率是 .14. 如图,反比例函数的图象经过菱形OABD的顶点A和边BD的一点C,且 , 若点D的坐标为(8,0),则k的值为 .
13. 一个不透明的布袋里装有3个只有颜色不同的球,其中1个红球,2个白球,从布袋里摸出1个球,则摸到的球是红球的概率是 .14. 如图,反比例函数的图象经过菱形OABD的顶点A和边BD的一点C,且 , 若点D的坐标为(8,0),则k的值为 .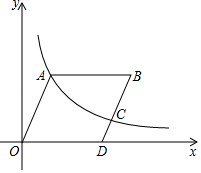 15. 如图,在正方形ABCD中, , M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N.连接NC交BD于点G.若BG:MG=3:5,则NG⋅CG的值为 .
15. 如图,在正方形ABCD中, , M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N.连接NC交BD于点G.若BG:MG=3:5,则NG⋅CG的值为 .
三、解答题
-
16. 计算:4cos30°﹣tan245°+|1|+2sin60°.17. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数的图象与性质,其探究过程如下:(1)、绘制函数图象,
列表:下表是x与y的几组对应值,其中m= .
x
…
﹣3
﹣2
﹣1
1
2
3
…
y
…
1
2
4
4
2
1
m
…
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出各点,请你描出剩下的点;
连线:用平滑的曲线顺次连接各点,已经画出了部分图象,请你把图象补充完整;
 (2)、通过观察图象,下列关于该函数的性质表述正确的是:;(填写代号)
(2)、通过观察图象,下列关于该函数的性质表述正确的是:;(填写代号)①函数值y随x的增大而增大;②关于y轴对称;③关于原点对称;
(3)、在上图中,若直线y=2交函数的图象于A,B两点(A在B左边),连接OA.过点B作BCOA交x轴于C.则= .18. 如图为某学校门口“测温箱”截面示意图,当身高1.7米的小聪在地面M处时开始显示额头温度,此时在额头B处测得A的仰角为45°,当他在地面N处时,此时在额头C处测得A的仰角为58°,如果测温箱顶部A处距地面的高度AD为3.3米,求B、C两点的距离.(结果保留一位小数,sin58°≈0.8,cos58°≈0.5,tan58°≈1.6) 19. 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长交BC的延长线于点F,且BF=BD.
19. 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长交BC的延长线于点F,且BF=BD. (1)、求证:AC为⊙O的切线;(2)、若CF=1,tan∠EDB=2,求⊙O的半径.20. 某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)、求证:AC为⊙O的切线;(2)、若CF=1,tan∠EDB=2,求⊙O的半径.20. 某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示. (1)、求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、设每月获得的利润为W(元).这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?21. 已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)、求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、设每月获得的利润为W(元).这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?21. 已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G. (1)、①如图1,若四边形ABCD是正方形,且DE⊥CF于G,则;
(1)、①如图1,若四边形ABCD是正方形,且DE⊥CF于G,则;②如图2,当四边形ABCD是矩形时,且DE⊥CF于G,AB=m,AD=n,则;
(2)、拓展研究:如图3,若四边形ABCD是平行四边形,且∠B+∠EGC=180°时,求证:;(3)、解决问题:如图4,若BA=BC=5,DA=DC=10,∠BAD=90°,DE⊥CF于G,请直接写出的值.22. 如图,在平面直角坐标系xOy中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C,其中A(﹣1,0),C(0,3). (1)、求该抛物线的解析式;(2)、如图1,点D,E是线段BC上的两点(E在D的右侧), , 过点D作DP∥y轴,交直线BC上方抛物线于点P,过点E作EF⊥x轴于点F,连接FD,FP,当△DFP面积最大时,求点P的坐标及△DFP面积的最大值;(3)、如图2,在(2)取得面积最大的条件下,连接BP,将线段BP沿射线BC方向平移,平移后的线段记为B'P',G为y轴上的动点,是否存在以B'P'为直角边的等腰Rt△GB'P'?若存在,请直接写出点G的坐标,若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、如图1,点D,E是线段BC上的两点(E在D的右侧), , 过点D作DP∥y轴,交直线BC上方抛物线于点P,过点E作EF⊥x轴于点F,连接FD,FP,当△DFP面积最大时,求点P的坐标及△DFP面积的最大值;(3)、如图2,在(2)取得面积最大的条件下,连接BP,将线段BP沿射线BC方向平移,平移后的线段记为B'P',G为y轴上的动点,是否存在以B'P'为直角边的等腰Rt△GB'P'?若存在,请直接写出点G的坐标,若不存在,请说明理由.